ห.ร.ม. มีประโยชน์

เราต่างก็รู้จัก ห.ร.ม. หรือ หารร่วมมากกันเป็นอย่างดี  ในทางคณิตศาสตร์ หารร่วมมากมีประโยชน์อย่างไร ตามมาดูกันเลย

          ห.ร.ม. มีประโยชน์กับวิชาคณิตศาสตร์ในเรื่อง เศษส่วน และการแก้โจทย์ปัญหา แต่ในบทความนี้    จะเป็นการนำประโยชน์ ห.ร.ม. ในเรื่อง เศษส่วน คือ การทำเศษส่วนให้เป็นเศษส่วนอย่างต่ำ โดยการหา     ห.ร.ม. ด้วยวิธีการตั้งหารหรือการหารสั้น

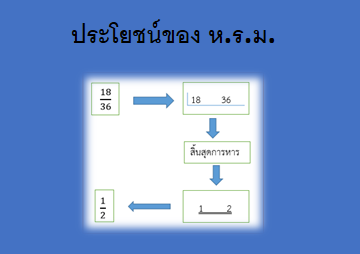ภาพที่ 1 ประโยชน์ของ ห.ร.ม.
ที่มา : ปิยวดี เอ่งฉ้วน

การหา ห.ร.ม. ในเรื่องเศษส่วน โดยการทำให้เป็นเศษส่วนอย่างต่ำ ด้วยการหารสั้นนั้น เนื่องจากเป็นวิธีที่ผู้เรียนส่วนมากมีความถนัด และมีความเป็นระเบียบเรียบร้อย ซึ่งความเป็นระเบียบเรียบร้อยของการ   หารสั้นนั้นทำให้เกิดความผิดพลาดได้น้อยที่สุดกับผู้เรียน และจะส่งผลต่อผู้เรียนในเรื่องความเป็นระเบียบเรียบร้อยในชีวิตประจำวันอีกด้วย

การทำเศษส่วนต่อไปนี้ให้เป็นเศษส่วนอย่างต่ำ

ตัวอย่าง  18/36  (เศษ 18 ส่วน 36)

ทำเป็นเศษส่วนอย่างต่ำ ด้วยการหารสั้น  จะได้

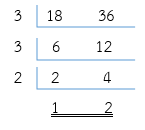
การหารสั้น ทำให้ทราบค่า ห.ร.ม. ของ 18 กับ 36 คือ 18 (3 × 3 × 2)  นำ 18 ไปหารทั้งตัวเศษและตัวส่วนจะได้ เท่ากับ  1/2  ซึ่งเป็นเศษส่วนอย่างต่ำของ  18/36

จากตัวอย่างที่ 1  จะเห็นได้ว่า ขั้นตอนกว่าจะได้เศษส่วนอย่างต่ำ จะต้องนำค่า ห.ร.ม. ไปหารทั้ง     ตัวเศษและตัวส่วนอีกกระบวนการหนึ่ง ซึ่งเป็นการเสียเวลา ถ้าสังเกตดี ๆ เราจะเห็นคำตอบตั้งแต่การหารสิ้นสุดแล้ว ดังภาพที่ 2

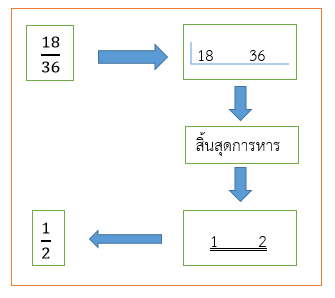
ภาพที่ 2 กระบวนการหาเศษส่วนอย่างต่ำ

ที่มา : ปิยวดี เอ่งฉ้วน

การนำประโยชน์ของ ห.ร.ม. ไปใช้ในเรื่องการบวกเศษส่วน

          เป็นการแสดงให้เห็นว่า ในการหา ห.ร.ม.  โดยการทำให้เป็นเศษส่วนอย่างต่ำ มีประโยชน์อย่างมากกับการบวกเศษส่วนในกรณีที่ตัวส่วนไม่เท่ากัน

ตัวอย่าง

( (11/121) + (33 x 11) ) มีค่าเท่ากับเท่าใด

*ในที่นี้  11/121 คือ เศษ 11 ส่วน 121

กรณีที่ 1

ขั้นตอนที่ 1 ทำตัวส่วนให้เท่ากัน โดยใช้ ค.ร.น. จะได้ ค.ร.น. เท่ากับ 484

ขั้นตอนที่ 2 ทำการบวกตัวส่วน คือ    ( (11/121) + (33 x 11) ) / 484  =  (44 + 363) / 484

= 407 / 484  (เศษ 407 ส่วน 484)

จากกรณีที่ 1 ทำให้ผู้เรียนมีความเข้าใจว่า  เป็นเศษส่วนอย่างต่ำแล้ว แต่จริง ๆ นั้นผู้เรียนยังสามารถทำให้เป็นเศษส่วนอย่างต่ำได้อีก ดูกรณีที่ 2

ขั้นตอนที่ 1  หา ห.ร.ม. ของ 11, 121 กับ 33, 44

จะเห็นได้ว่า จากตัวอย่างที่ 4 ในกรณีที่ 2  ห.ร.ม. เป็นสิ่งสำคัญในการบวกเศษส่วน เพราะทำให้เป็นเศษส่วนอย่างต่ำที่ถูกต้อง ซึ่งจะเกิดประโยชน์กับผู้เรียนเป็นอย่างมาก จากตัวอย่างที่ 4 กรณีที่ 1 ผู้เรียนมักจะเกิดการผิดพลาดเพราะเข้าใจว่าเป็นคำตอบที่ถูกต้อง ไม่สามารถทำเป็นเศษส่วนอย่างต่ำได้อีก อันที่จริงแล้ว  เศษ 407 ส่วน 484 สามารถนำ 11 มาหารทั้งตัวเศษและตัวส่วนได้  ทั้งนี้ขึ้นอยู่กับผู้เรียนต้องฝึกฝนการทำโจทย์อย่างสม่ำเสมอจนเกิดความชำนาญ

บทความนี้ ต้องการให้ผู้สนใจได้เล็งเห็นถึงประโยชน์ของ ห.ร.ม. ว่ามีประโยชน์ในการนำไปใช้งานในเรื่องเศษส่วน การหา ห.ร.ม. ด้วยการหารนั้น จะเห็นได้ว่า เป็นวิธีหนึ่งที่ได้คำตอบอย่างรวดเร็วและมีความเป็นระเบียบเรียบร้อย ซึ่งจะส่งผลให้เกิดความผิดพลาดน้อยที่สุด สามารถตรวจสอบได้ง่าย รวมทั้งดูสะอาดตา

ซึ่งอาจสรุปได้ว่า ประโยชน์ของ  ห.ร.ม. มีดังต่อไปนี้คือ

         1. ทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำ

         2. การหาผลบวกและผลลบของเศษส่วน  โดยทำส่วนให้เท่ากัน

         3. ใช้คำนวณการแบ่งสิ่งของที่มีจำนวนไม่เท่ากันออกเป็นส่วนๆ ที่เท่ากันที่มีจำนวนมากที่สุด

4. ใช้ในการคำนวณงานบางอย่างที่ใช้เวลาต่างกัน  และหาเวลาที่จะทำพร้อมกันในครั้งต่อไป

แหล่งที่มา

ธนาคารความรู้.ประโยชน์ของ หรม. สืบค้นเมื่อ 20 มิถุนายน 2562. จาก https://sites.google.com/site/nonzero69/surasak/prayochn-khxng-h-rm

ตัวหารร่วมมาก. สืบค้นเมื่อ 20 มิถุนายน 2562. จาก https://th.wikipedia.org/wiki/ตัวหารร่วมมาก

การนำหรมไปใช้. สืบค้นเมื่อ 20 มิถุนายน 2562. จาก https://sathaporn2510.wordpress.com/about/การนำหรมไปใช้/