ค่ามาตรฐาน (statistics)
ค่ามาตรฐาน หมายถึง การเปรียบเทียบค่าของข้อมูลตั้งแต่สองค่าขึ้นไปที่มาจากข้อมูลคนละชุดมีความแตกต่างกันหรือไม่เพียงไร อาจมีมาตราวัดที่แตกต่างกันหรือมีหน่วยต่างกัน
บางครั้งไม่สามารถเปรียบเทียบโดยตรงได้ ทั้งนี้เนื่องจากค่าเฉลี่ยเลขคณิตของข้อมูลแต่ละชุดและส่วนเบี่ยงเบนมาตรฐานมักจะไม่เท่ากัน เช่น ต้องการเปรียบเทียบผลการเรียนวิชาภาษาอังกฤษและวิชาคณิตศาสตร์ของนักเรียนคนใดคนหนึ่งในชั้นว่า
เรียน วิชาไหนดีกว่ากัน แม้ว่าจะทำได้โดยดูจากคะแนนสอบของวิชาทั้งสองโดยปรับให้มีคะแนนเต็มเท่ากัน ถ้าคะแนนสอบของวิชาใดดีกว่าก็สรุปผลว่านักเรียนคนนั้นเรียนวิชานั้นได้ดี กว่า ซึ่งจะเห็นได้ว่าเป็นการสรุปผลที่ยังไม่ถูกต้องนักเพราะค่าเฉลี่ยเลขคณิต หรือส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบวิชาทั้งสองของนักเรียนทั้งหมดในชั้น อาจจะไม่เท่ากัน ทั้งนี้อาจจะเนื่องมาจากเนื้อหาหรือข้อสอบของทั้งสองวิชามีความยากง่ายต่าง กัน หรือครูผู้สอนแต่ละวิชามีวิธีการสอนที่จะทำให้นักเรียนมีความเข้าใจในวิชา นั้นๆ ต่างกัน เป็นต้น ดั้งนั้นเพื่อที่จะให้การเปรียบเทียบมีความถูกต้องมากขึ้น จึงมีความจำเป็นต้องแปลงคะแนนของวิชาทั้งสองที่นักเรียนคนนั้นสอบได้ให้เป็น คะแนนมาตรฐานหรือค่ามาตรฐาน (ซึ่งมีค่าเฉลี่ยเลขคณิตแต่ละส่วนเบี่ยงเบนมาตรฐานเท่ากันเสียก่อน) โดยใช้สูตรค่ามาตรฐานแล้วจึงเปรียบเทียบคะแนนวิชาทั้งสอง การแปลงค่าข้อมูลของตัวแปรแต่ละตัวให้เป็นค่ามาตรฐานนี้โดยทั่วไปคือ การเปลี่ยนแปลงข้อมูลให้เป็นค่ามาตรฐานที่มีค่าเฉลี่ยเลขคณิตเท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 1
หรือ Zi = Xi-X เมื่อ i คือ 1,2,…, n
s
โดยที่ Xi แทน ค่าที่ i ของตัวแปร X
X แทน ค่าเฉลี่ยเลขคณิตของตัวอย่าง
S แทน ส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง
n แทน จำนวนตัวอย่าง
ตัวอย่างที่ 5.6 นักเรียนคนหนึ่งสอบวิชาภาษาอังกฤษและวิชาคณิตศาสตร์ซึ่งมีคะแนนเต็ม 100 คะแนนเท่ากัน ได้ 72 คะแนน และ 75 คะแนน ตามลำดับ ถ้าค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบวิชาภาษาอังกฤษของนักเรียนห้องนี้เป็น 70 และ 10 คะแนน และของคะแนนสอบวิชาคณิตศาสตร์เป็น 73 และ 16 คะแนน ตามลำดับ จงเปรียบเทียบดูว่านักเรียนคนนี้เรียนรายวิชาไหนดีกว่ากัน
วิธีทำ จากค่ามาตรฐานของ Xi คือ
จะได้ ค่ามาตรฐานของคะแนนสอบวิชาภาษาอังกฤษ = 72-70
10
ค่ามาตรฐานของคะแนนสอบวิชาภาษาอังกฤษ = 0.20
ค่ามาตรฐานของคะแนนสอบวิชาคณิตศาสตร์ = 72-73
16
ค่ามาตรฐานของคะแนนสอบวิชาคณิตศาสตร์ = 0.125
ดังนั้น ค่ามาตรฐานของคะแนนสอบวิชาภาษาอังกฤษของนักเรียนคนนี้สูงกว่าค่ามาตรฐานของคะแนนสอบวิชาคณิตศาสตร์ แสดงว่านักเรียนคนนี้เรียนวิชาภาษาอังกฤษได้ดีกว่าวิชาคณิตศาสตร์ ตอบ
ตัวอย่างที่ 5.7 คะแนนสอบวิชาภาษาไทยของนักศึกษาห้องหนึ่งมีค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานเป็น 73 และ 16 ตามลำดับ ถ้าค่ามาตรฐานของคะแนนสอบวิชานี้ของนักเรียนคนหนึ่งในห้องนี้ คือ 0.2 อยากทราบว่านักเรียนคนนี้สอบได้กี่คะแนน
นั่นคือ นักเรียนคนนี้สอบวิชาคณิตศาสตร์ได้ 76.2 คะแนน ตอบ
ตัวอย่างที่ 5.8 ในการสอบปรากฏค่าเฉลี่ยของการสอบเป็น 80 คะแนน ส่วนเบี่ยงเบนมาตรฐานเป็น 10 และในการตัดสินใจผลสอบผู้ที่ได้คะแนนมาตรฐานตั้งแต่-1 จะถือว่าสอบผ่าน ปรากฏว่ามีนักเรียนคนหนึ่งสอบได้ 75 คะแนน ต้องการทราบว่านักเรียนคนนี้สอบผ่านหรือสอบตก
วิธีทำ จากสูตร Zi = Xi-X
ดังนั้นจะได้ว่า Zi = 75-80
10
= -5
10
Zi = -0.5
ดั้งนั้น นักเรียนคนนี้สอบผ่าน เนื่องจากค่า Z มากกว่า-1 ตามเกณฑ์การตัดสินผลสอบ
ตัวอย่างค่ามาตรฐานหรือคะแนนมาตรฐาน (Standard Scores)
ค่ามาตรฐานเป็นค่าที่บอกให้ทราบความแตกต่างระหว่างค่าของข้อมูลนั้นกับค่าเฉลี่ยเลขคณิตของข้อมูลชุดนั้นเป็นกี่เท่า ของส่วนเบี่ยงเบนมาตรฐาน
สูตร Zi = 
เมื่อ Zi คือ คะแนนมาตรฐาน
XI คือ คะแนนดิบของข้อมูลที่มีค่าเฉลี่ยเลขคณิตที่จะแปลเป็นคะแนนมาตรฐาน
คือ ค่าเฉลี่ยเลขคณิต
S.D. คือ ส่วนเบี่ยงเบนมาตรฐาน
ในการเปรียบเทียบค่าคะแนนของข้อมูลที่มาจากข้อมูลต่างชุดกัน ว่าจะมีความแตกต่างกันอย่างไร ซึ่งบางครั้งไม่สามารถเปรียบเทียบได้โดยตรง เพราะค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของข้อมูลมักจะไม่เท่ากัน ในการเปรียบเทียบให้มีความถูกต้องจึงมีความจำเป็นต้องมีการเปลี่ยน คะแนนของข้อมูลทั้งสองชุดให้เป็นค่ามาตรฐาน( ซึ่งมีค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐาน เท่ากันเสียก่อน ) จึงจะเปรียบเทียบข้อมูล 2 ชุดนี้ได้ ในการเปลี่ยนค่าของข้อมูลของตัวแแปรหรือข้อมูลแต่ละตัวให้เป็นค่ามาตรฐานที่นิยมใช้คือเปลี่ยนให้มีค่าเฉลียเลขคณิตเท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 1
ข้อสังเกต
1.คะแนนมาตรฐานเป็นตัวเลขไม่มีหน่วย
2.ส่วนเบี่ยงเบนมาตรฐานของคะแนนมาตรฐานทั้งหมดของชุดข้อมูล จะมีค่าเท่ากับ 1
3.คะแนนมาตรฐานของข้อมูลใดๆ จะเป็นบวก หรือลบก็ได้ขึ้นอยู่กับค่าของข้อมูลนั้นๆ กับมัชฌิมเลขของข้อมูลชุดนั้นว่าค่าใดมีค่ามากกว่ากัน
4.คะแนนมาตรฐานโดยทั่วไปจะมีค่า – 3 ถึง +3 แต่อาจจะมีบางข้อมูลที่มีคะแนนมาตรฐานสูงหรือต่ำกว่านี้เล็กน้อย
5.เมื่อแปลงข้อมูลทุกๆ ค่าในข้อมูลชุดใดชุดหนึ่งให้เป็นคะแนนมาตรฐานแล้วทำค่ามาตรฐานเหล่านั้นมาคำนวณหาค่ามัชฌิมเลขคณิตจะได้เท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานจะได้เท่ากับ 1 ( คะแนนมาตรฐานจะมีมัชฌิมเลขคณิตเท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 1 )
6. จะได้ Z > 0 และ จะได้ Z< 0
Ex1. สมศักดิ์สอบวิชาสถิติและภาษาอังกฤษ ซึ่งมีคะแนนเต็ม 100 คะแนนเท่ากัน ในการสอบสายใจได้คะแนน 75 และ 85 คะแนนตามลำดับ ถ้าค่ามัชฌิมเลขคณิตและส่วนเเบี่ยงเบนมาาตรฐานของคะแนนสถิติของนักศึกษากลุ่มนี้คือ 60 และ 10 ค่าเลขคณิตและส่วนเฉลี่ยเบี่ยงเบนมาตรฐานของวิชาภาษาอังกฤษคือ 70 และ 12 ตามลำดับ แล้วจงเปรียบเทียบว่าสมศักดิ์เรียนวิชาไหนได้ดีกว่ากัน
วิธีทำ
สูตร Zi =
ค่ามาตรฐานของคะแนนวิชาสถิติ คือ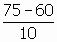 
= 1.5
ค่ามาตรฐานของคะแนนวิชาภาษาอังกฤษ คือ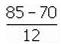 
= 1.25
ค่ามาตรฐานของคะแนนวิชาสถิติของสมศักดิ์สูงกว่าค่ามาตรฐานของคะแนนวิชาภาษาอังกฤษ แสดงว่าสมศักดิ์เรียนวิชาสถิติได้ดีกว่าวิชาภาษาอังกฤษ
Ex2. ในการสอบวิชาบัญชีของนักศึกษาระดับปวส.ของวิทยาลัยอาชีวศึกษาสุโขทัย มีค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานเป็น 64 และ 10 ตามลำดับ ถ้าค่ามาตรฐานของคะแนนวิชาบัญชีของ นารีคือ 1.3 อยากทราบว่านารีสอบได้คะแนนเท่าไร
วิธีทำ
สูตร Zi =
แทนค่า 1.3 =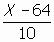 
X =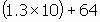 
= 77
นารีสอบวิชาบัญชีได้คะแนน 77 คะแนน
ค่ามาตรฐาน
ค่ามาตรฐาน หมายถึง การเปรียบเทียบค่าของข้อมูลตั้งแต่สองค่าขึ้นไปที่มาจากข้อมูลคนละชุดมีความแตกต่างกันหรือไม่เพียงไร อาจมีมาตราวัดที่แตกต่างกันหรือมีหน่วยต่างกัน
บางครั้งไม่สามารถเปรียบเทียบโดยตรงได้ ทั้งนี้เนื่องจากค่าเฉลี่ยเลขคณิตของข้อมูลแต่ละชุดและส่วนเบี่ยงเบนมาตรฐานมักจะไม่เท่ากัน เช่น ต้องการเปรียบเทียบผลการเรียนวิชาภาษาอังกฤษและวิชาคณิตศาสตร์ของนักเรียนคนใดคนหนึ่งในชั้นว่า
เรียน วิชาไหนดีกว่ากัน แม้ว่าจะทำได้โดยดูจากคะแนนสอบของวิชาทั้งสองโดยปรับให้มีคะแนนเต็มเท่ากัน ถ้าคะแนนสอบของวิชาใดดีกว่าก็สรุปผลว่านักเรียนคนนั้นเรียนวิชานั้นได้ดี กว่า ซึ่งจะเห็นได้ว่าเป็นการสรุปผลที่ยังไม่ถูกต้องนักเพราะค่าเฉลี่ยเลขคณิต หรือส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบวิชาทั้งสองของนักเรียนทั้งหมดในชั้น อาจจะไม่เท่ากัน ทั้งนี้อาจจะเนื่องมาจากเนื้อหาหรือข้อสอบของทั้งสองวิชามีความยากง่ายต่าง กัน หรือครูผู้สอนแต่ละวิชามีวิธีการสอนที่จะทำให้นักเรียนมีความเข้าใจในวิชา นั้นๆ ต่างกัน เป็นต้น ดั้งนั้นเพื่อที่จะให้การเปรียบเทียบมีความถูกต้องมากขึ้น จึงมีความจำเป็นต้องแปลงคะแนนของวิชาทั้งสองที่นักเรียนคนนั้นสอบได้ให้เป็น คะแนนมาตรฐานหรือค่ามาตรฐาน (ซึ่งมีค่าเฉลี่ยเลขคณิตแต่ละส่วนเบี่ยงเบนมาตรฐานเท่ากันเสียก่อน) โดยใช้สูตรค่ามาตรฐานแล้วจึงเปรียบเทียบคะแนนวิชาทั้งสอง การแปลงค่าข้อมูลของตัวแปรแต่ละตัวให้เป็นค่ามาตรฐานนี้โดยทั่วไปคือ การเปลี่ยนแปลงข้อมูลให้เป็นค่ามาตรฐานที่มีค่าเฉลี่ยเลขคณิตเท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 1
หรือ Zi = Xi-X เมื่อ i คือ 1,2,…, n
s
โดยที่ Xi แทน ค่าที่ i ของตัวแปร X
X แทน ค่าเฉลี่ยเลขคณิตของตัวอย่าง
S แทน ส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง
n แทน จำนวนตัวอย่าง
ตัวอย่างที่ 5.6 นักเรียนคนหนึ่งสอบวิชาภาษาอังกฤษและวิชาคณิตศาสตร์ซึ่งมีคะแนนเต็ม 100 คะแนนเท่ากัน ได้ 72 คะแนน และ 75 คะแนน ตามลำดับ ถ้าค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบวิชาภาษาอังกฤษของนักเรียนห้องนี้เป็น 70 และ 10 คะแนน และของคะแนนสอบวิชาคณิตศาสตร์เป็น 73 และ 16 คะแนน ตามลำดับ จงเปรียบเทียบดูว่านักเรียนคนนี้เรียนรายวิชาไหนดีกว่ากัน
วิธีทำ จากค่ามาตรฐานของ Xi คือ
จะได้ ค่ามาตรฐานของคะแนนสอบวิชาภาษาอังกฤษ = 72-70
10
ค่ามาตรฐานของคะแนนสอบวิชาภาษาอังกฤษ = 0.20
ค่ามาตรฐานของคะแนนสอบวิชาคณิตศาสตร์ = 72-73
16
ค่ามาตรฐานของคะแนนสอบวิชาคณิตศาสตร์ = 0.125
ดังนั้น ค่ามาตรฐานของคะแนนสอบวิชาภาษาอังกฤษของนักเรียนคนนี้สูงกว่าค่ามาตรฐานของคะแนนสอบวิชาคณิตศาสตร์ แสดงว่านักเรียนคนนี้เรียนวิชาภาษาอังกฤษได้ดีกว่าวิชาคณิตศาสตร์ ตอบ
ตัวอย่างที่ 5.7 คะแนนสอบวิชาภาษาไทยของนักศึกษาห้องหนึ่งมีค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานเป็น 73 และ 16 ตามลำดับ ถ้าค่ามาตรฐานของคะแนนสอบวิชานี้ของนักเรียนคนหนึ่งในห้องนี้ คือ 0.2 อยากทราบว่านักเรียนคนนี้สอบได้กี่คะแนน
นั่นคือ นักเรียนคนนี้สอบวิชาคณิตศาสตร์ได้ 76.2 คะแนน ตอบ
ตัวอย่างที่ 5.8 ในการสอบปรากฏค่าเฉลี่ยของการสอบเป็น 80 คะแนน ส่วนเบี่ยงเบนมาตรฐานเป็น 10 และในการตัดสินใจผลสอบผู้ที่ได้คะแนนมาตรฐานตั้งแต่-1 จะถือว่าสอบผ่าน ปรากฏว่ามีนักเรียนคนหนึ่งสอบได้ 75 คะแนน ต้องการทราบว่านักเรียนคนนี้สอบผ่านหรือสอบตก
วิธีทำ จากสูตร Zi = Xi-X
ดังนั้นจะได้ว่า Zi = 75-80
10
= -5
10
Zi = -0.5
ดั้งนั้น นักเรียนคนนี้สอบผ่าน เนื่องจากค่า Z มากกว่า-1 ตามเกณฑ์การตัดสินผลสอบ
-ขอบคุณ แหล่งข้อมูล http://www.stvc.ac.th/elearning/stat/csu4.html
