การดำเนินการของเซต

เซตพื้นฐาน

เซตเป็นหัวข้อที่มีความสำคัญและแทรกอยู่ในเนื้อหาของคณิตศาสตร์แทบทุกส่วน เราใช้เซตในการรวบรวมสิ่งต่าง ๆ ไม่ว่าจะเป็น ค่าตัวเลข ตัวแปร ที่มีคุณสมบัติเหมือนกันไว้ด้วยกันเป็นประโยชน์ต่อการจำแนกประเภทของสิ่งต่าง ๆ ออกเป็นกลุ่ม

ภาพที่ 1 สับเซตทั้งหมดของเซตที่มีสมาชิก 3 ตัว
ที่มา วีระ ยุคุณธร

การกำหนดเซต

การรวบรวมสิ่งต่าง ๆเข้าด้วยกันเรียกว่าเซต สิ่งที่อยู่ในเซตเราเรียกว่าสมาชิกเช่นเซต A ประกอบด้วยสมาชิก 5 ตัวได้แก่ a, e, i, o, u กล่าวได้ว่า a เป็นสมาชิกของเซต A แต่ b ไม่เป็นสมาชิกของเซต A ประโยคภาษาข้างต้นสามารถเปลี่ยนเป็นสัญลักษณ์ทางคณิตศาสตร์ได้ดังนี้

ตารางที่ 1 แสดงการแทนข้อความการเป็นสมาชิกของเซตแบบแจงแจกสมาชิกด้วยสัญลักษณ์

การเขียนเซตในตารางที่ 1 เราเรียกว่าการกำหนดเซตแบบแจกแจงสมาชิกนิยมใช้เมื่อเราต้องการระบุสมาชิกของเซต แต่บางกรณีที่เราไม่ต้องการแจกแจงสมาชิกหรือไม่สามารถระบุสมาชิกที่แน่นอนได้ จึงมีวิธีการกำหนดเซตในลักษณะของการบอกคุณสมบัติมีหลักการดังนี้ กำหนดให้ A เป็นเซตที่มีคุณสมบัติ P นั้นคือสำหรับ x ใดๆที่เป็นสมาชิกใด ๆของ A แล้ว x จะต้องมีคุณสมบัติ P เขียนแทนด้วยสัญลักษณ์ตัวตารางต่อไปนี้

ตารางที่ 2 แสดงการแทนข้อความการเป็นสมาชิกของเซตแบบมีเงื่อนไขด้วยสัญลักษณ์

จากตัวอย่างข้างต้นเราสามารถกล่าวได้ว่า A เป็นเซตที่รวบรวมอักษรสระในภาษาอังกฤษกล่าวคือ ถ้า x เป็นสมาชิกใด ๆของเซต A แล้ว x จะต้องเป็นตัวอักษรภาษาอังกฤษ ในขณะเดียวกันหากไม่ใช่สมาชิกของเซต A ย่อมไม่ใช่ตัวอักษรในภาษาอังกฤษการใช้สัญลักษณ์ในตารางที่ 2 สื่อความหมายดังตารางต่อไปนี้

ตารางที่ 3 ตัวอย่างการแปรความหมายสัญลักษณ์การเป็นสมาชิกของเซต

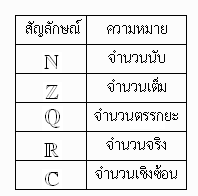
ในบางครั้งจะมีการกำหนดสัญลักษณ์ของเซตที่ถูกกล่าวถึงอยู่บ่อยครั้งเช่นในระบบจำนวนเรากำหนดสัญลักษณ์ของจำนวนดังนี้

ตารางที่ 4 สัญลักษณ์ของเซตในระบบจำนวน

ขนาดของเซต

การรวบรวมวัตถุต่าง ๆเป็นเซต ถ้าจำนวนสมาชิกที่อยู่ในเซตมีจำนวนมากย่อมส่งผลให้เซตมีขนาดใหญ่ตามไปด้วย ดังนั้นคุณสมบัติพื้นฐานในการวัดขนาดของเซตคือ เซตนั้นจะต้องเป็นเซตที่สามารถนับจำนวนสมาชิกได้เรียกว่า เซตนับได้ พิจารณาเซตต่อไปนี้ กำหนดให้ A = {x, x เป็นจำนวนเต็มที่อยู่ระหว่าง -10 และ 10} และ B = {x, x เป็นจำนวนเต็มที่มากกว่า 10} จะเห็นว่าทั้ง A และ B สามารถเขียนแจงแจงสมาชิกได้ดังนี้ A = { -10,-9,-8,…,8,9,10 } และ B = { 10, 11 ,12, …} จะเห็นว่า A และ B เป็นเซตนับได้โดยที่ A มีสมาชิก 20 ตัว แต่ B มีจำนวนสมาชิกเป็นอนันต์ สำหรับเซตที่ไม่มีสมาชิกเรียกว่า เซตว่าง กล่าวได้ว่าเซตว่างเป็นเซตที่มีจำนวนสมาชิก 0 ตัว ดังนั้นเซตนับได้ยังสามารถจำแนกได้เป็นอีกสองประเภทคือ เซตที่มีจำนวนสมาชิกเป็นจำนวนเต็มบวกหรือศูนย์เรียกว่า เซตจำกัด และเซตที่มีสมาชิกมากมายนับไม่ถ้วนเรียกว่าเซตอนันต์ ส่วนการใช้สัญลักษณ์บอกขนาดของเซตแสดงดังตารางต่อไปนี้

ตารางที่ 5 ตัวอย่างการแปรความหมายสัญลักษณ์จำนวนสมาชิกของเซต

ความสัมพันธ์ระหว่างเซตสองเซต

การพิจารณาขนาดและสมาชิกของเซต 2 เซตทำให้เราสามารถบอกความสัมพันธ์ระหว่างเซตทั้งสองเซตได้ตัวอย่างเช่นกำหนดให้ A = {x, x เป็นจำนวนเต็มบวกที่มีค่าไม่เกิน 10 และ 2หารได้ลงตัว} และ B = { x, x=2k เมื่อ k = 1,2,3,4,5 } จะเห็นว่าเซต A และ เซต B ถูกกำหนดด้วยภาษาที่แตกต่างกันแต่เมื่อพิจารณาสมาชิกแล้วจะพบว่าทั้งเซต A และ เซต B เขียนแจงแจงสมาชิกได้คือ { 2, 4, 6, 8, 10 } นั้นหมายความว่า เซต A และ เซต B เป็นเซตเดียวกันนิยามด้วยการเท่ากันของเซตดังนี้

A = B ก็ต่อเมื่อ สามาชิกทุกตัวของเซต A เป็นสมาขิกของเซต B และ สมาชิกทุกตัวของเซต B เป็นสมาชิกของเซต A

สังเกตได้ว่า A และ B จะต้องมีจำนวนสมาชิกเท่ากัน และเป็นชุดเดียวกันแต่ถ้าหาก A และ B มีจำนวนสมาชิกเท่ากันแต่มีสมาชิกในเซตแตกต่างกันแล้วจะกล่าวว่า เซต A และ เซต B เป็นเซตที่เทียบเท่ากันนิยามดังนี้

A ~ B ก็ต่อเมื่อ n(A) = n(B)

กำหนดให้ A = { x, x เป็นอักษรสระของภาษาอังกฤษ } และ B = { 1, 2, 3, 4, 5 } จะเห็นว่า n(A) = 5 = n(B) ดังนั้น A และ B เป็นเซตที่เทียบเท่ากัน สังเกตว่าเซตจำกัดที่มีสมาขิก k ตัวเทียบเท่ากับเซต {1,2,3,…,k } เสมอ

ในกรณีที่สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B แต่ n(A) น้อยกว่า n(B) เรากล่าวว่า เซต A เซตย่อยแท้ของเซต B แต่ถ้า n(A) น้อยกว่าหรือเท่ากับ n(B) จะกล่าวว่า เซต A เป็นเซตย่อยของเซต B ตัวอย่างเช่นถ้ากำหนดให้ B = { 1,2,3,4,5 } ถ้า A = { 1,4,5 } จะเห็นว่าสมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และ เซต A มีขนาดเล็กกว่า เซต B สรุปได้ว่า A เป็นเซตย่อยแท้ของเซต B แต่ถ้ากำหนดให้ A ={ 1,3,9 } จะเห็นว่ามีสมาชิกบางตัวของเซต A ไม่ใช่สมาชิกในเซต B เราสรุปได้ว่า A ไม่เป็นเซตย่อยของเซต B

เราให้นิยามความสัมพันธ์เชิงเซตย่อยของเซตสองเซตได้ดังนี้

A เป็นเซตย่อยของ B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B

A เป็นเซตย่อยแท้ของ B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และ n(A) ไม่เท่ากับ n(B)