พื้นที่ผิวและปริมาตรของพีระมิด
- การเรียกชื่อพีระมิด
การเรียกชื่อพีระมิด นิยมเรียกชื่อตามลักษณะรูปเหลี่ยมของฐาน ตัวอย่างเช่น พีระมิดฐานสี่เหลี่ยมผืนผ้า พีระมิดฐานหกเหลี่ยม เป็นต้น
- ส่วนประกอบของพีระมิด
พีระมิดแบ่งออกเป็น 2 ลักษณะ คือ พีระมิดตรงและพีระมิดเอียง
พีระมิดตรง หมายถึง พีระมิดที่มีฐานเป็นรูปเหลี่ยมด้านเท่ามุมเท่า มีสันยาวเท่ากันทุกเส้น จะมีสูงเอียงทุกเส้นยาวเท่ากัน และส่วนสูงตั้งฉากกับฐานที่จุดซึ่งอยู่ห่างจากจุดยอดมุมของรูปเหลี่ยมที่เป็นฐานเป็นระยะเท่ากัน มีหน้าทุกหน้าเป็นรูปสามเหลี่ยมหน้าจั่ว ส่วนกรณีที่สันทุกสันยาวไม่เท่ากัน สูงเอียงทุกเส้นยาวไม่เท่ากัน เรียกว่า พีระมิดเอียง
ปริซึม
ในทางคณิตศาสตร์ ให้ความหมายคำว่า ปริซึม ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานทั้งสองเป็นรูปเหลี่ยมที่เท่ากันทุกประการ ฐานทั้งสองอยู่บนระนาบเดียวกัน และด้านข้างแต่ละด้านเป็นรูปสี่เหลี่ยมด้านขนาน หรือเรียกง่ายๆว่า แท่งเหลี่ยมตัน
สูตรคำนวณต่างๆที่เกี่ยวกับปริซึม
ปริมาตรของปริซึม = พื้นที่ฐาน X ความสูง
พื้นที่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง X พื้นที่หน้าตัดหัวท้าย
พื้นที่ผิวข้างของปริซึม = ความยาวเส้นรอบฐาน X ความสูง
พีระมิด
ในทางคณิตศาสตร์ ให้ความหมายคำว่า พีระมิด ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยู่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น เรียกว่า พีระมิด
สูตรคำนวณต่างๆที่เกี่ยวกับพีระมิด
พื้นที่ผิวข้างของพีระมิด = 1/2 X ความยาวรอบฐาน X สูงเอียง
= พื้นที่ของหน้าทุกหน้ารวมกัน
พื้นที่ผิวของพีระมิด = พื้นที่ผิวข้างของพีระมิด X พื้นที่ฐานของพีระมิด
ทรงกระบอก
ในทางคณิตศาสตร์ให้ความหมายคำว่า ทรงกระบอก ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยุ่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ เรียกรูปเรขาคณิตสามมิตินั้นว่า ทรงกระบอก
สูตรคำนวณต่างๆที่เกี่ยวกับทรงกระบอก
ปริมาตรทรงกระบอก = (22/7 หรือ 3.14) X รัศมียกกำลัง 2 X สูงตรง
พื้นที่ผิวข้างของทรงกระบอก = 2(22/7 หรือ 3.14) X รัศมี X สูงตรง + 2(22/7 หรือ 3.14) X รัศมียกกำลัง 2
กรวย
ในทางคณิตศาสตร์ให้ความหมายคำว่า กรวย ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง เรียกรูปเรขาคณิตสามมิตนั้นว่า กรวย
สูตรคำนวณต่างๆที่เกี่ยวข้องกับกรวย
ปริมาตรของกรวย = 1/3 X (22/7 หรือ 3.14) X รัศมียกกำลังสอง X สูงตรง
พื้นที่ผิวของกรวย = (22/7 หรือ 3.14) X รัศมี X สูงเอียง + (22/7 หรือ 3.14) X รัศมียกกำลังสอง
ทรงกลม
ในทางคณิตศาสตร์ให้ความหมายคำว่า ทรงกลม ดังนี้
รูปเรขาคณิตสามมิติที่มีผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดจุดหนึ่งเป็นระยะเท่ากัน เรียกว่า ทรงกลม
จุดคงที่นั้นเรียกว่า จุดศูนย์กลางของทรงกลม
ระยะที่เท่ากันนั้นเรียกว่า รัศมีของทรงกลม
สูตรคำนวณต่างๆที่เกี่ยวข้องกับทรงกลม
ปริมาตรของทรงกลม = 4/3 X (22/7 หรือ 3.14) X รัศมียกกำลัง 3
พื้นที่ผิวของทรงกลม = 4 X (22/7 หรือ 3.14) X รัศมียกกำลัง 2
*ข้อสังเกต
1) พีระมิดตรงจะมีฐานเป็นรูปเหลี่ยมด้านเท่า และมีสันทุกเส้นยาวเท่ากัน
2) พีระมิดตรงที่มีฐานเป็นรูปเหลี่ยมด้านเท่ามุมเท่า จะมีสูงเอียงทุกเส้นยาวเท่ากัน
3) ส่วนสูงของพีระมิดตรงใดๆ จะตั้งฉากกัับฐาน ที่จุดซึ่งอยู่่ห่างจากมุมของรูปเหลี่ยมที่เป็นฐาน เป็นระยะเท่ากัน
4) พีระมิดที่มีหน้าทุกหน้าเป็นรูปสามเหลี่ยมหน้าจั่ว จะมีสันทุกเส้นยาวเท่ากัน
- การหาความยาวด้านต่างๆ ของพีระมิด
การจะหาพื้นที่ผิวและปริมาตรของพีระมิดได้นั้น ควรจะหาความยาวด้านต่างๆ ของพีระมิดให้ได้เสียก่อน
** การหาความยาวด้านต่างๆ มักใช้ทฤษฎีบทปีทาโกรัส
3.1) การหาความสูงเอียง กรณีที่โจทย์กำหนดความยาวสัน
Ex.1 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 6 นี้ว สันยาว 5 นิ้ว จงหาความสูงเอียง
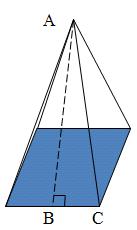
วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน
กำหนดให้ AC เป็นสันยาว 5 นิ้ว และ AB เป็นความสูงเอียง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 6 ÷ 2 = 3 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB2 + 32 = 52
AB2 = 52 – 32
AB2 = 16
AB = 4
ตอบ สูงเอียงยาว 4 นิ้ว
3.2) การหาความสูงเอียง กรณีที่โจทย์กำหนดส่วนสูง
Ex.2 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นี้ว ส่วนสูงยาว 12 นิ้ว จงหาความสูงเอียง
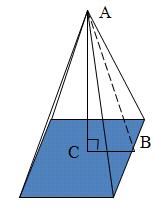
วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน
กำหนดให้ AC เป็นส่วนสูง ยาว 12 นิ้ว และ AB เป็นความสูงเอียง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = 13
ตอบ สูงเอียงยาว 13 นิ้ว
3.3) การหาความสูง กรณีโจทย์กำหนดสูงเอียง
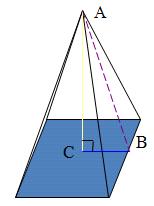
Ex.3 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นิ้ว สูงเอียงยาว 13 นิ้ว จงหาความสูง
วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน
ให้ AB เป็นความสูงเอียง, AC เป็นส่วนสูง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AC2 + 52 = 132
AC2 = 169 – 25
AC2 = 144
AC = 12
ตอบ ส่วนสูงยาว 12 นิ้ว






