ปริมาณเวกเตอร์ (Vector quantity)
เป็นปริมาณที่มีทั้งขนาดและทิศทาง การคำนวณมีวิธีการที่ต่างจากการคำนวณในระบบจำนวนธรรมดา เพื่อความสะดวกในการคำนวณ จึงมีการกำหนดสัญลักษณ์ ใช้แทนปริมาณเวกเตอร์ โดยกำหนดว่า ความยาวแทนขนาดของเวกเตอร์ และหัวลูกศรชี้ทิศทางของเวกเตอร์ การคำนวณปริมาณเวกเตอร์ที่นักเรียนในช่วงชั้นนี้ควรทราบ คือ
การบวกเวกเตอร์
การคูณเวกเตอร์ (สำหรับนักเรียนที่เลือกเรียนวิชาฟิสิกส์เป็นวิชาเพิ่มเติม)
การเรียกชื่อหรือเขียนชื่อของเวกเตอร์นิยมเขียนแทนด้วยสัญลักษณ์ ดังนี้ หรือ
เวกเตอร์ศูนย์ คือ เวกเตอร์ที่ไม่มีขนาดและทิศทาง แทนด้วยจุด
เวกเตอร์ที่เท่ากันต้องมีขนาดยาวเท่ากันและทิศทางไปทางเดียวกัน
เวกเตอร์ที่ขนาดเท่ากันแต่ทิศทางตรงกันข้าม ถือว่าเป็นเวกเตอร์ที่ไม่เท่ากัน และเครื่องหมายตรงกันข้าม เช่น
ขนาด 4 หน่วยทิศไปทางเหนือ ขนาด 4 หน่วยทิศไปทางใต้ เป็นต้น

การบวกเวกเตอร์ ทำได้ 2 วิธี คือ
-วิธีวาดรูป
-วิธีคำนวณ
วิธีวาดรูป เป็นวิธีการเขียนรูปเวกเตอร์ตัวตั้งด้วยลูกศรให้มีขนาดและทิศทางตามที่กำหนด แล้วเขียนลูกศรแทน เวกเตอร์ที่นำมาบวกต่อหัวลูกศรของตัวตั้ง หากมีเวกเตอร์ที่นำมาบวกอีกก็เขียนลูกศรต่อไปอีกจนครบ แล้วจึงลากเส้นจากหางลูกศรที่เป็นตัวตั้งตัวแรกไปยังปลายของลูกศรที่นำมาวาดต่อหลังสุด วัดความ ยาวของเส้นที่ลากนี้ จะได้ขนาดของเวกเตอร์ที่เป็นผลลัพธ์และทิศทางของเวกเตอร์ลัพธ์มีทิศจากจุด ตั้งต้นของเวกเตอร์ตัวตั้งไปยังปลายของเวกเตอร์สุดท้าย หรืออาจกล่าวได้ว่า เวกเตอร์ลัพธ์เป็นด้าน สุดท้ายที่มาปิดให้ได้รูปเหลี่ยมครบ
วิธีคำนวณ แยกเป็นวิธีย่อย ๆ ได้ดังนี้
เวกเตอร์ที่ขนานกัน ถ้ามีทิศทางเดียวกันนำขนาดมาบวกกัน ทิศทางของเวกเตอร์ลัพธ์ไปทางเดิม ถ้าเวกเตอร์มีทิศทางตรงกันข้ามนำขนาดของเวกเตอร์มาลบกัน เวกเตอร์ลัพธ์มีทิศทางไปทางเวกเตอร์ที่มีค่ามากกว่า
เวกเตอร์ที่ตั้งฉากกัน ให้นำเวกเตอร์ทั้งมาบวกกัน โดยชุดที่ทิศทางขนานกันไว้ด้วยกัน จะได้ผลบวกของเวกเตอร์สองชุดตั้งฉากกัน นำผลบวกทั้งสองชุดมาคำนวณโดยใช้ทฤษฎีพีทากอรัส ดังสูตรต่อไปนี้
ให้ เป็นผลบวกของเวกเตอร์ในแนวแกน X
เป็่นผลบวกของเวกเตอร์ในแนวแกน Y
ขนาดของเวกเตอร์ลัพธ์ เท่ากับ
ทิศทางของเวกเตอร์ลัพธ์จะทำมุมกับแกน X ซึ่งมีค่า tan ของมุมนั้นเท่ากับ
เวกเตอร์ที่ไม่ตั้งฉากกัน ในกรณีนี้จะต้องทราบขนาดของมุมระหว่างเวกเตอร์กับแกน X หรือแกน Y จึงจะคำนวณได้ วิธีการคือ หาองค์ประกอบของเวกเตอร์ในแนวแกน X และแกน Y ของแต่ละเวกเตอร์ ดังรูป
หลังจากนั้นนำองค์ประกอบแต่ละแกนมารวมกัน จะเหลือเวกเตอร์เพียงสองเวกเตอร์ตั้งฉากกัน หลังจากนั้นจึงหาผลบวกของเวกเตอร์ตามวิธีที่เวกเตอร์ตั้งฉากกัน

การคูณเวกเตอร์ มีสองวิธีคือ
Dot Product ผลคูณของเวกเตอร์ เป็นปริมาณสเกลลาร์
ขนาดของผลคูณหาได้จากสมการ
โดยที่ A และ B เป็นขนาดของเวกเตอร์ที่นำมาคูณกัน
เป็นมุมระหว่างเวกเตอร์ที่นำมาคูณกัน
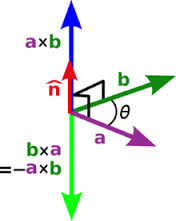
Croos Product ผลคูณของเวกเตอร์ เป็นปริมาณเวกเตอร์
ขนาดของผลคูณหาได้จากสมการ
โดยที่ A และ B เป็นขนาดของเวกเตอร์ที่นำมาคูณกัน
เป็นมุมระหว่างเวกเตอร์ที่นำมาคูณกัน
ทิศทางของเวกเตอร์ที่เป็นผลลัพธ์หาจากการใช้กฏมือขวาดังนี้
” แบมือขวาออกให้นิ้วทั้งสี่ชี้ไปทางทิศของเวกเตอร์ตัวตั้ง งอนิ้วทั้งสี่ไปหาทิศของเวกเตอร์ที่เป็นตัวคูณ หัวแม่มือชี้ทิศของเวกเตอร์ลัพธ์”