จำนวนจริง (Real number)-พีชคณิตระดับมัธยม

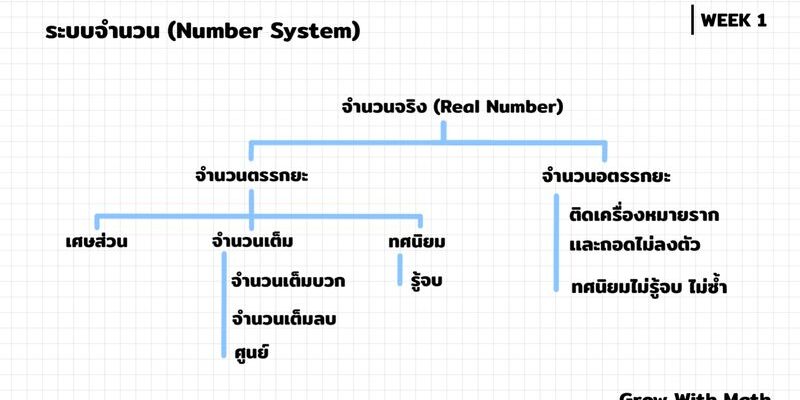
จำนวนจริง

ตัวเลขเป็นสัญลักษณ์ที่มนุษย์ใช้แทนปริมาณต่างที่มีอยู่ในธรรมชาติ ในยุคเริ่มแรกเรารู้จักจำนวนที่มีลักษณะเต็มหน่วยที่เป็นปริมาณเชิงประจักษ์ในธรรมชาติ ชุดจำนวนเหล่านี้ถูกนำมารวมกันเป็นเซตเรียกว่าเซตจำนวนนับ (Natural numbers) ต่อมามีการกำหนดเลขศูนย์ และจำนวนตรงกันข้ามกับจำนวนนับ จึงเรียกจำนวนสามกลุ่มนี้ใหม่ว่า จำนวนเต็มบวก จำนวนเต็มศูนย์ และจำนวนเต็มลบ เกิดเป็นเซตจำนวนเต็ม ต่อมามีการศึกษาปริมาณเชิงสัดส่วน (Ratio) ที่เกิดจากการแบ่งในลักษณะการหารกันระหว่างจำนวนเต็ม รวมถึงการการหาผลหารที่อยู่รูปทศนิยมรู้จบ และทศนิยมไม่รู้จบชนิดทศนิยมซ้ำ เมื่อผนวกกับระบบจำนวนที่มีก่อนหน้าเราเรียกเซตจำนวนกลุ่มนี้ว่าเซตจำนวนตรรกยะ (Rational numbers) สำหรับจำนวนที่อยู่นอกเหนือจากจำนวนตรรกยะเรียกว่าเซตจำนวนอตรรกยะ ผลผนวกสุดท้ายทำให้เราได้เซตจำนวนที่เรียกว่าเซตจำนวนจริง ระบบจำนวนจริงนี้สามารถอธิบายเป็นภาพด้วยเส้นจำนวนแสดงการจัดเรียงอันดับ และการวัดระยะระหว่างตำแหน่งสองตำแหน่งเมื่อเราแทนตำแหน่งด้วยจุดบนเส้นจำนวน

1.1.1 เซตจำนวนจริง

จากที่กล่าวมาข้างต้นเซตจำนวนนับเป็นชุดตัวเลขชุดแรกสุดที่มนุษย์สัมผัสได้ การมีอยู่ของจำนวนนับจึงเป็นสัจพจน์ เรียกว่าสัจพจน์ของเปอาโนว่าด้วยการมีอยู่ของยูนิตแทนด้วยสัญลักษณ์ 1 และพจน์ตามของ 1 (1*) แทนด้วย 2 ซึ่งมีเพียงพจน์เดียว โดยการอุปนัยเชิงคณิตศาสตร์ทำให้ได้ 3, 4, 5,… เกิดเป็นเซตจำนวนนับนั้นคือ

เซตของจำนวนนับ N = { 1, 2, 3, … }

หากเราพิจารณาการบวกด้วย 1 จะพบว่า

a + 1 = a* และ a + 1* = a + 1 + 1 = (a + 1)*

พิจารณา

3 + 2 = 3 + 1* = (3+1)* = 4* = 5

การบวกด้วย 2 จึงเป็นการเพิ่มที่ละ 1 จำนวนสองครั้ง เป็นที่ทราบกันดีว่าการเพิ่มทำให้ปริมาณเพิ่มขึ้น และการลดทำให้ปริมาณลดลง คำถามที่น่าสนใจคือการเพิ่มที่ทำให้ปริมาณยังคงเท่าเดิม และการเพิ่มที่ทำให้ปริมาณมีค่าน้อยลงคือจำนวนใดในเซตของจำนวนนับ { 1, 2, 3, … } ซึ่งพบว่าเซตดังกล่าวไม่มีเพียงต่อการตอบคำถามว่า 1 + x = 1 แล้ว x คือจำนวนใด จึงมีการเพิ่มจำนวนศูนย์ { 0 } ซึ่งใช้อธิบายตัวบวกที่ทำให้ผลบวกยังคงมีค่าเท่าเดิมเรียกว่าเอกลักษณ์การบวก เมื่อรวม 0 เข้าในไปเซตจำนวนนับจะได้จำนวนทั้งหมด

          W = {0,1,2,…}

สำหรับตัวเพิ่มที่ทำให้มีค่าลดลงเป็นศูนย์คือถ้า 1 + x = 0 แล้ว x เป็นจำนวนใดเราจึงสร้าง (-1) เมื่อตอบคำถามที่ว่า 1 + (-1) = 0 ในทำนองเดียวกัน 2 + x = 0 จึงมี -2 ดังนั้นสำหรับ  {1,2,3,…} จะต้องสร้างกลุ่มจำนวน

{-1,-2,-3, ….} เป็นเซตของจำนวนตรงกันข้ามกับ {1,2,3,…}

เมื่อนำชุดตัวเลขมารวมกันจะได้ {…,-2,-1,0,1,2,…} เป็นเซตจำนวนเต็มจำแนกเป็น 3 กลุ่มได้แก่

เซตจำนวนเต็ม             Z = {…,-2,-1,0,1,2,…}

เซตจำนวนเต็มบวก        Z⁺ = {1,2,3,…}

เซตจำนวนเต็มศูนย์        Z⁰ = {0}

เซตจำนวนเต็มลบ         Z^– = {-1,-2,-3,…}

สำหรับการคูณในเซตจำนวนเต็มจะเห็นว่าไม่ว่านำจำนวนใดก็ตามสองจำนวนมาคูณกัน ผลคูณจะยังคงอยู่ในเซต แต่สำหรับการหารเราแบ่งพิจารณาเป็นการหารด้วยศูนย์ การหารด้วย 1 และ -1 และ การหารด้วยจำนวนที่เหลือ

การหารด้วยศูนย์ไม่สามารถกำหนดค่าผลหารหรือนิยามความหมายได้ดังนั้น การหารด้วยศูนย์จึงไม่นิยาม ในระบบพีชคณิตเราจะเรียกพจน์ที่มีการหารด้วย 0 ว่า พจน์ที่ไม่นิยาม (undefined term)

การหารด้วยหนึ่งจะทำให้จำนวนเดิมดังนั้นชุดจำนวน {…,-2,-1,0,1,2,…} เพียงพอสำหรับการหาผลหารด้วย 1 รวมไปถึง -1 ด้วยซึ่งจะทำให้เกิดผลลัพธ์เป็นจำนวนตรงกันข้าม

การหารด้วยจำนวนอื่น ๆ ที่ไม่ใช่ -1, 0 และ 1 จะทำให้เกิดจำนวนชนิดใหม่ที่ไม่ใช่จำนวนเต็ม นิยามเขียนแทนด้วยเศษส่วนเช่น 1/2 , 5/3, -7/6 เป็นต้น หากเราใช้วิธีการตั้งหารยาวเปลี่ยนเศษส่วนเป็นทศนิยมจะพบว่าผลหารจะอยู่ในรูปของทศนิยมรู้จบ และทศนิยมไม่รู้จบชนิดทศนิยมซ้ำ

จะเห็นว่า Z = {…,-2,-1,0,1,2,…} สามารถเขียนได้ในรูปเศษด้วยโดยการหารด้วย 1 เมื่อผนวกเข้าเศษส่วนที่เกิดจากการนำจำนวนเต็มหารจำนวนเต็มเราจะได้ชุดจำนวนที่แสดงสัดส่วนเรียกว่าจำนวนตรรกยะ

จำนวนตรรกยะ Q = { a/b , a และ b เป็นจำนวนเต็ม โดยที่ b ไม่เป็นศูนย์ }

ข้อสังเกตของจำนวนตรรกยะคือจำนวนที่มีค่าเท่ากับ 1/2 มีได้หลายค่าเช่น 2/4, -3/6 เป็นต้นแต่อย่างไรก็ตามหากพิจารณาเศษส่วนอย่างต่ำนั้นจะเขียนได้เพียงแบบเดียวนั้นคือ a/b จะเป็นเศษส่วนอย่างต่ำเมื่อตัวหารร่วมมากของ a และ b มีค่าเท่ากับ 1

อย่างไรก็ตามยังมีจำนวนอื่น ๆ ที่อยู่น้องเหนือจากจำนวนตรรกยะเช่นในทฤษฎีพิธากอรัสถ้าเราวาดสามเหลี่ยมมุมฉากที่มีด้านประกอบมุมฉากยาวด้านละหนึ่งหน่วยเมื่อวัดความยาวด้านตรงข้ามมุมฉากเราไม่สามารถระบุขนาดที่แจ่มชัดได้ อีกนัยนึงสังเกตได้ว่าหากเราพิจารณา

x² = 0 เราจะพบว่า x = 0

x² = 1 เราจะพบว่า x = -1 หรือ x = 1

x² = 2 เราจะพบว่า ด้วยระบบจำนวนตรรกยะไม่สามารถตอบคำถามนี้ได้

x² = 3 เราจะพบว่า ด้วยระบบจำนวนตรรกยะไม่สามารถตอบคำถามนี้ได้เช่นกัน

x² = 4 เราจะพบว่า x = -2 หรือ x = 2

พบว่าถ้า x² = 0, 1, 4, 9, 16, … จะมีจำนวนตรรกยะที่เป็นคำตอบของ x แต่หากพิจารณา x² = 2, 3, 5 เป็นต้นเราจะต้องสร้างจำนวนเรียกว่า กรณฑ์ ซึ่งเท่ากับเป็นจำนวนสำหรับตอบคำถาม x² = 2 นอกจากนี้ยังมีปริมาณอื่นเช่น ค่าพาย และ ค่า e ซึ่งเป็นชุดตัวเลขนอกเหนือจากจำนวนตรรกยะเรียกว่า อตรรกยะเขียนแทนด้วย Q^c

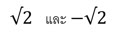
                เราจึงรวมเซตของจำนวนตรรกยะและอตรรกยะเข้าด้วยกันเรียกว่าจำนวนจริง ( R )

-ขอบคุณข้อมูล https://www.scimath.org/