แผนภาพเวนน์-ออยเลอร์
แผนภาพออยเลอร์(Eulerdiagram)เป็นแผนภาพที่ใช้ในการอธิบายความสัมพันธ์ของเซตต่างๆโดยให้วงกลมแต่ละวงแทนแต่ละเซตและแสดงความสัมพันธ์ของแต่ละเซตด้วยการครอบซึ่งแสดงความเป็นสับเซตการทับซ้อนกันหรือการไม่ทับซ้อนกันซึ่งแสดงว่าทั้งสองเซตไม่มีความสัมพันธ์กัน ลักษณะแผนภาพวงกลมเช่นนี้เชื่อว่าถูกใช้ครั้งแรกโดยนักคณิตศาสตร์ชาวสวิสนามว่าเลออนฮาร์ดออยเลอร์แผนภาพออยเลอร์นั้นมียังลักษณะคล้าย คลึงกันกับแผนภาพเวนน์มากในทฤษฎีเซตซึ่งเป็นแขนงหนึ่งของคณิตศาสตร์จึงนิยมใช้แผนภาพประยุกต์จากแผนภาพทั้งสองในการอธิบายเซตต่าง ๆ ให้เข้าใจได้ง่ายยิ่งขึ้น แผนภาพเวนน์–ออยเลอร์เป็นแผนภาพแสดงความเกี่ยวข้องของเซตต่าง ๆ ซึ่งชื่อที่ใช้เรียกเป็นชื่อของนักคณิตศาสตร์สองคน คือ จอห์น เวนน์ และ เลโอนาร์ด ออยเลอร์
การเขียนแผนภาพเวนน์–ออยเลอร์
การเขียนแผนภาพเวนน์–ออยเลอร์มักเขียนแทนเอกภพสัมพัทธ์U ด้วยสี่เหลี่ยมผืนผ้าหรือรูปปิดใดๆ ส่วนเซต A,B,C,D,… ซึ่งเป็นเซตย่อยของ Uอาจเขียนแทนด้วยวงกลมหรือวงรีหรือรูปปิดใดๆโดยให้ภาพที่แทนเซตย่อยอยู่ในรูปสี่เหลี่ยมผืนผ้าที่แทนเอกภพสัมพัทธ์
การพิจารณาเกี่ยวกับเซตจะง่ายขึ้น ถ้าเราใช้แผนภาพของเวนน์-ออยเลอร์ เข้ามาช่วย หลักการเขียนแผนภาพมีดังนี้
1. ใช้รูปสี่เหลี่ยมผืนผ้าหรือสี่เหลี่ยมมุมฉากแทนเอกภพสัมพัทธ์
2. ใช้วงกลมหรือวงรีหรือรูปปิดใด ๆ แทนเซตต่าง ๆ ที่เป็นสมาชิกของ และเขียนภายในสี่เหลี่ยมผืนผ้า

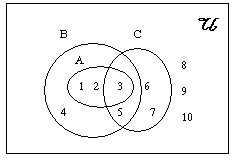
ถ้ากำหนดให้ U = {1,2,3,4,5,6,7,8,9,10} A = {1,2,3} , B = {1,2,3,4,5} , C = {3,5,6,7}
เราจะเขียนแผนภาพเวนน์–ออยเลอร์ แสดงเอกภพสัมพัทธ์ U และเซตย่อยต่าง ๆ ดังแผนภาพต่อไปนี้
การใช้แผนภาพเวนน์–ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล
เราจะวาดแผนภาพตามสมมติฐานที่เป็นไปได้ แล้วพิจารณาว่าแผนภาพแต่ละกรณีแสดงผลสรุปตามที่สรุปไว้หรือไม่ ถ้าทุกกรณีแสดงผลตามที่กหนด แสดงว่าสมเหตุสมผล ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปนั้นไม่สมเหตุสมผล โดยจะใช้การอ้างเหตุผลโดยตรรกบทของตรรกศาสตร์เข้ามาตรวจสอบ
ในการใช้แผนภาพเพื่อตรวจสอบความสมเหตุสมผล จะต้องวาดแผนภาพตามเหตุผลหรือสมมติฐานทุกกรณีที่เป็นไปได้ ถ้าทุกกรณีแสดงผลตามที่กำหนด จะได้ว่าข้อสรุปนั้น สมเหตุสมผล แต่ถ้ามีบางกรณีที่ไม่สอดคล้องกับผลสรุปแล้ว ผลสรุปนั้นจะไม่สมเหตุผมผล …

ภาพจาก Mayitutoryou
มาดูแผนภาพของเวนน์-ออยเลอร์ เป็นแผนภาพที่ใช้แสดงความเกี่ยวข้องของเซต เพื่อช่วยในการคิดคำนวณหรือแก้ปัญหา ซึ่งตัวชื่อแผนภาพตามชื่อของนักคณิตศาสตร์คือ เวนน์และออยเลอร์ การเขียนแผนภาพเวนน์-ออยเลอร์ มีวิธีการเขียนดังนี้
ให้ เอกภพสัมพทธ์ U แทนด้วยรูปสี่เหลี่ยมผืนผ้าหรือรูปปิดใด ๆ
เซต A, B, C, . . . ซึ่งเป็นสับเซตของ U แทนด้วยวงกลม วงรี หรือรูปปิดอื่น ๆ โดยให้เซต A, B, C, . . . อยู่ใน U ดังตัวอย่าง
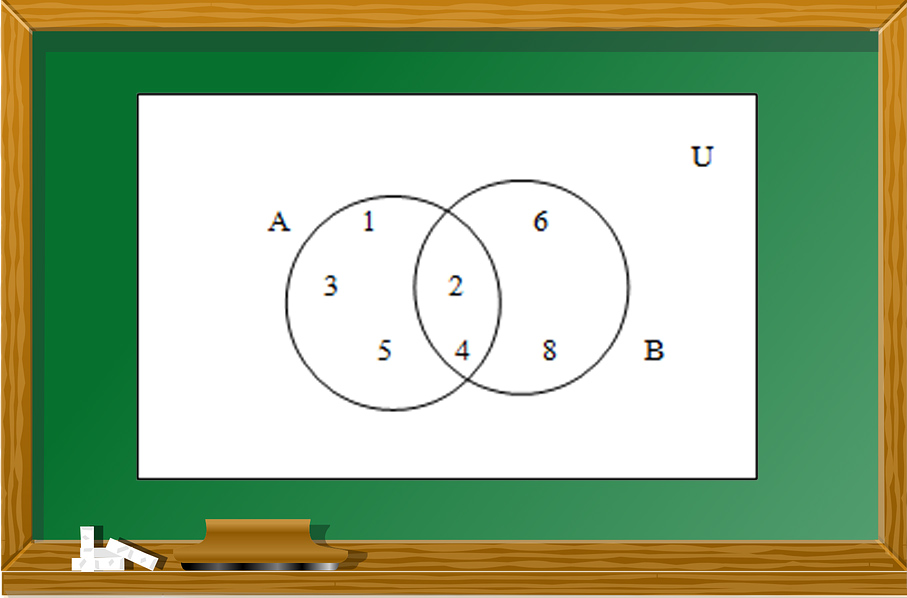
ตัวอย่างที่ 1 กำหนด U = {1, 2, 3, . . .} , A = {1, 2, 3, 4, 5} และ B = {2, 4, 6, 8}
จงเขียนแผนภาพของเวนน์-ออยเลอร์แทนเซต
วิธีทำ เซต A และเซต B มีสมาชิกร่วมกันคือ 2 และ 4 ซึ่งสามารถเขียนแผนภาพ
แทนเซต A และ B ได้ดังนี้
ตัวอย่างที่ 2 กำหนด U = {a, b, c, . . . , z} , A = {a, b, c, d} , B = {e, f, g}
และ C = {h, i, j, k} จงเขียนแผนภาพเวนน์-ออยเลอร์
วิธีทำ เขียนแผนภาพเวนน์-ออยเลอร์ แทน A, B และ C ได้ดังนี้

ตัวอย่างที่ 3 กำหนด U = {x | x เป็นจำนวนนับที่น้อยกว่า 20}
A = {x | x เป็นจำนวนนับที่น้อยกว่า 10}
B = {x | x เป็นจำนวนคี่บวกที่น้อยกว่า 7}
จงเขียนแผนภาพเวนน์-ออยเลอร์
วิธีทำ U = {x | x เป็นจำนวนนับที่น้อยกว่า 20}
\ U = {1, 2, 3, . . . , 19}
A = {x | x เป็นจำนวนนับที่น้อยกว่า 10}
\ A = {1, 2, 3, . . . , 9}
B = {x | x เป็นจำนวนคี่บวกที่น้อยกว่า 7}
\ B = {1, 3, 5}
เขียนแผนภาพแทน A และ B ได้ดังนี้
การใช้แผนภาพเวนน์–ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล
เราจะวาดแผนภาพตามสมมติฐานที่เป็นไปได้ แล้วพิจารณาว่าแผนภาพแต่ละกรณีแสดงผลสรุปตามที่สรุปไว้หรือไม่ ถ้าทุกกรณีแสดงผลตามที่กหนด แสดงว่าสมเหตุสมผล ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปนั้นไม่สมเหตุสมผล โดยจะใช้การอ้างเหตุผลโดยตรรกบทของตรรกศาสตร์เข้ามาตรวจสอบ
ในการใช้แผนภาพเพื่อตรวจสอบความสมเหตุสมผล จะต้องวาดแผนภาพตามเหตุผลหรือสมมติฐานทุกกรณีที่เป็นไปได้ ถ้าทุกกรณีแสดงผลตามที่กำหนด จะได้ว่าข้อสรุปนั้น สมเหตุสมผล แต่ถ้ามีบางกรณีที่ไม่สอดคล้องกับผลสรุปแล้ว ผลสรุปนั้นจะไม่สมเหตุผมผล

ภาพจาก Mayitutoryou by พี่เมย์
-ขอบคุณข้อมูล https://www.scimath.org/






