เวกเตอร์ (vector)

เวกเตอร์ ปริมาณมี 2 แบบ คือสเกลาร์ กับเวกเตอร์
สเกลาร์ เป็น ปริมาณที่มีแต่ขนาด เช่น พื้นที่ อุณหภูมิ ความยาว เป็นต้น
เวกเตอร์ เป็น ปริมาณที่มีทั้งขนาดและทิศทาง เช่นความเร็ว แรง เป็นต้น
เราสามารถแทนเวกเตอร์ในเชิงเรขาคณิตได้ด้วยส่วนของเส้นตรงและลูกศร โดยที่ทิศทางของลูกศรแทนทิศทางของเวกเตอร์ และความยาวของลูกศรแทน ขนาดของเวกเตอร์ หางลูกศรเรียกว่า จุดเริ่มต้นของเวกเตอร์ หัวลูกศร เรียกว่า จุดสิ้นสุดของเวกเตอร์

สัญลักษณ์ที่ใช้

(รูปที่ 1)

บทนิยาม  1  ถ้าเวกเตอร์  u และ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ แล้ว ผลบวกของเวกเตอร์  u และ v เขียนแทนด้วยเวกเตอร์  u + v  หาได้จากให้ตำแหน่งเวกเตอร์ v มีจุดเริ่มต้นอยู่ที่จุดสิ้นสุดของเวกเตอร์ u
เวกเตอร์ u + v  จะแทนด้วยลูกศรจากจุดเริ่มต้นของเวกเตอร์ u  ไปยังจุดสิ้นสุดของเวกเตอร์  v ดังรูปที่  2

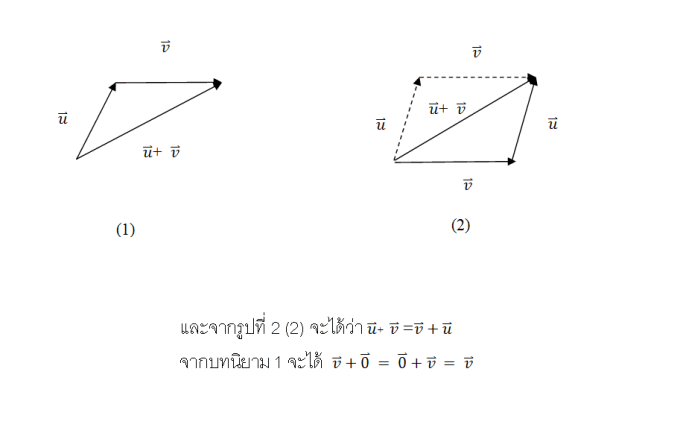(รูปที่ 2)

บทนิยาม 2 ให้เวกเตอร์ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ และ k เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ แล้ว เวกเตอร์  kv หมายถึงเวกเตอร์ที่มีขนาดเท่ากับ |k| เท่าของเวกเตอร์ v เมื่อ k>0 เวกเตอร์ kv จะมีทิศทางเดียวกับ v และเมื่อ k<0 เวกเตอร์ kv มีทิศตรงข้ามกับเวกเตอร์ v และให้เวกเตอร์  kv =0 เมื่อ k =0

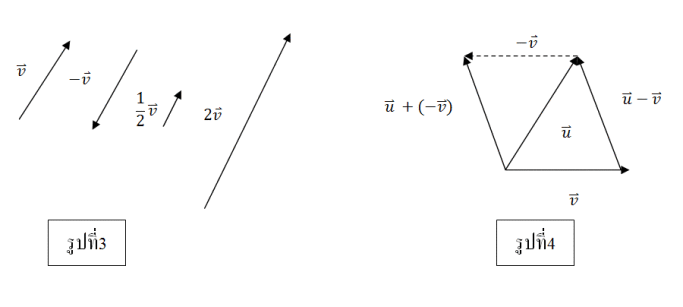จากรูปที่  3 ได้ว่าเวกเตอร์  v กับเวกเตอร์  Kv เป็นเวกเตอร์ที่ขนานกัน

เวกเตอร์ในระบบพิกัดฉากในปริภูมิสามมิติ

            ให้เวกเตอร์ v เป็นเวกเตอร์ในปริภูมิ 3 มิติในระบบพิกัดฉาก ซึ่งมีจุดเริ่มต้นอยู่ที่จุดกำเนิด และจุดสิ้นสุดอยู่ที่จุด (x₁,y₁,z₁) ดังรูปที่ 5 เรียกพิกัด x₁,y₁และ z₁ว่า ส่วนประกอบเวกเตอร์ และเขียนแทนด้วย

 

 

 

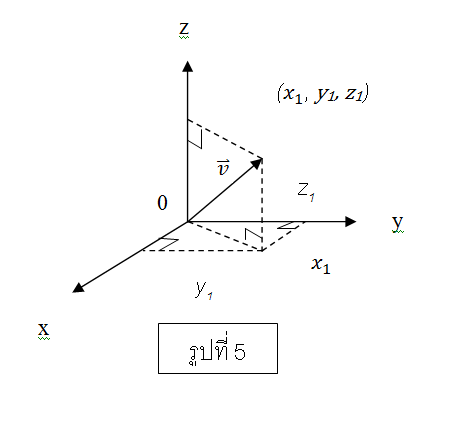
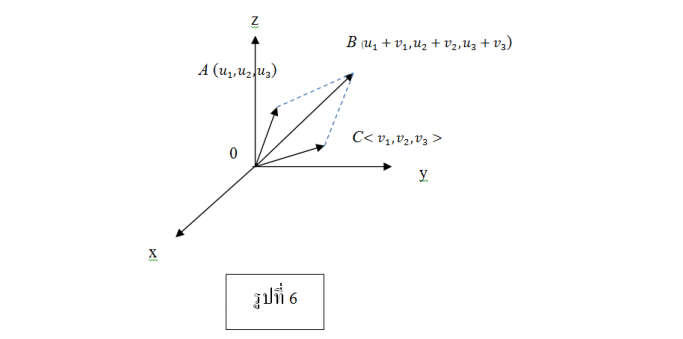
ตัวอย่าง 2 กำหนดให้ จุด A(1, 2, 3) ,B(4, -1, -2)และ C(-3, 4, 0)

            จะได้เวกเตอร์    AB = <4,-1,-2> – <1,2,-3> = <3,-3,1>

                     เวกเตอร์     BC = <-3,4,0> – <4,-1,-2> = <-7,5,2>

ขนาดของเวกเตอร์

ขนาดของเวกเตอร์ u เขียนแทนด้วยสัญลักษณ์ จะได้ว่า  ‖u‖  ขนาดของเวกเตอร์  u เรียกอีกอย่างว่า ค่าประจำของเวกเตอร์ u

 

 

ตัวอย่างที่ 4  กำหนดให้เวกเตอร์ u = <2, -1, -2>

1. เวกเตอร์หนึ่งหน่วยที่มีทิศเดียวกับเวกเตอร์ u

2. เวกเตอร์ที่มีขนาดเป็น 5 หน่วยทิศตรงข้ามกับเวกเตอร์ u

                                   

 

 

-ขอบคุณแหล่งข้อมูล https://kulazaza.wordpress.com