การเคลื่อนที่แบบโพรเจกไทล์

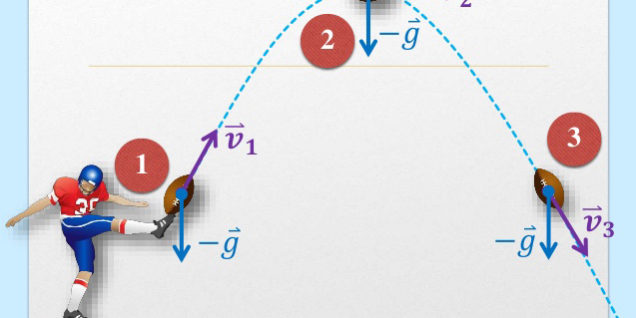
การเคลื่อนที่แบบโพรเจกไทล์ หมายถึง การเคลื่อนที่ของวัตถุที่ประกอบด้วยการเคลื่อนที่ 2 แนวตั้งฉากกัน และเกิดขึ้นในเวลาเดียวกัน เช่น การขี่จักรยานผาดโผน เป็นเส้นทางโค้งจากเนินด้านหนึ่งไปยังเนินอีกด้านหนึ่ง การเคลื่อนที่ของวัตถุที่ถูกขว้างขึ้นไปในอากาศในแนวที่ทำมุม θ ใด ๆ กับแนวราบด้วยอัตราเร็ว u เราสามารถวิเคราะห์ความเร็วการเคลื่อนที่ของวัตถุออกมาได้ดังภาพ

ภาพที่ 2 แสดงแนวการเคลื่อนที่และความเร็วที่ตำแหน่งใด ๆ
ที่มา : กัญญา เกื้อกูล

ความเร็วต้นในแนวราบ = ucos θ

และ ความเร็วต้นในแนวดิ่ง = usin θ

การที่วัตถุมีความเร็วต้นถึงสองแนวเช่นนี้ ทำให้วัตถุมีการเคลื่อนที่ในแนวทั้งสองพร้อมกัน คือ การเคลื่อนที่ในแนวราบและการเคลื่อนที่ในแนวดิ่ง เมื่อรวมการเคลื่อนที่ทั้งสองนี้เข้าด้วยกัน แนวการเคลื่อนที่ของวัตถุที่ปรากฏจะเป็นวิถีโค้งในอากาศ

เนื่องจากการเคลื่อนที่แบบโพรเจกไทล์ประกอบไปด้วยการเคลื่อนที่ใน 2 แนว ทำให้แบ่งการคำนวณเกี่ยวกับการเคลื่อนที่แบบโพรเจกไทล์ออกได้เป็น 2 ส่วนคือ การคำนวณในแนวราบและการคำนวณในแนวดิ่ง

การวิเคราะห์การเคลื่อนที่แบบโพรเจกไทล์ในแนวราบ

โดยทั่วไป การคำนวณกรณีของการขว้างวัตถุขึ้นไปในอากาศด้วยความเร็วต้น u และทำมุม θ ใด ๆ กับแนวราบเราจะพิจารณาโดยถือว่าไม่มีแรงมากระทำต่อวัตถุในแนวราบ เราจึงพิจารณาการเคลื่อนที่นี้เช่นเดียวกับการเคลื่อนที่ของวัตถุด้วยความเร็วคงที่ และใช้สมการคำนวณเป็นดังนี้

ระยะทาง = อัตราเร็ว × เวลา

การวิเคราะห์การเคลื่อนที่แบบโพรเจกไทล์ในแนวดิ่ง

ภาพที่ 3 การเปรียบเทียบระยะทางในแนวดิ่งระหว่างวัตถุที่มีการเคลื่อนที่แบบโพรเจกไทล์และการเคลื่อนที่ในแนวดิ่งอย่างเสรีของวัตถุ
ที่มา : กัญญา เกื้อกูล

จากภาพที่ 3 แสดงการการเปรียบเทียบระยะทางในแนวดิ่งของวัตถุที่มีการเคลื่อนที่ในแนวดิ่งอย่างเสรีด้วยความเร็วต้นเท่ากับศูนย์ กับวัตถุที่มีการเคลื่อนที่แบบโพรเจกไทล์ที่มีความเร็วต้นอยู่ในแนวระดับ อันมีผลทำให้ความเร็วต้นในแนวดิ่งของวัตถุมีค่าเป็นศูนย์เช่นกัน โดยวัตถุทั้ง 2 ในภาพเริ่มต้นเคลื่อนที่พร้อมกันจากภาพแสดงให้เห็นว่า เมื่อเวลาผ่านไป ระยะทางในแนวดิ่งของวัตถุทั้งสองเท่ากันทุกขณะ ทั้งนี้ทั้งการเคลื่อนที่ในแนวดิ่งอย่างเสรีและการเคลื่อนแบบโพรเจกไทล์ ต่างก็เป็นการเคลื่อนที่ภายใต้แรงความโน้มถ่วงของโลก

ดังนั้นจึงสรุปได้ว่า การคำนวณในส่วนแนวดิ่งของวัตถุที่เคลื่อนที่แบบโพรเจกไทล์ทำได้ โดยใช้วิธีการคำนวณของการเคลื่อนที่ในแนวดิ่งอย่างเสรี นั่นคือ

1) ต้องกำหนดเครื่องหมายของปริมาณเวกเตอร์ทุกชนิด

2) ความเร่งของวัตถุมีค่าเท่ากับ g ซึ่งมีทิศลงเสมอ

จากที่กล่าวมาจะเห็นได้ว่า การคำนวณในแนวราบและแนวดิ่งต่างก็เป็นอิสระซึ่งกันและกันซึ่งถ้าทราบความเร่งในแต่ละแนวแล้วก็สามารถหาปริมาณต่าง ๆ ในแนวนั้นได้จากสมการของการเคลื่อนที่ในแนวตรง ได้แก่

การคำนวณหาระยะทางในแนวราบ

จากการพิจารณาการเคลื่อนที่แบบโพรเจกไทล์ที่มีความเร็วต้น u ทำมุม θ กับแนวราบ การเคลื่อนที่นี้มีอัตราเร็วต้นในแนวราบและแนวดิ่งเป็น ucosθ และ usinθ ตามลำดับ

สำหรับการเคลื่อนที่ในแนวดิ่ง เมื่อกำหนดให้ปริมาณเวกเตอร์ที่มีทิศลงเป็นบวก ก็จะคำนวณหาเวลาของการเคลื่อนที่ได้จากสมการ

แทนค่าโดยให้ s_y เป็นระยะทางในแนวดิ่ง จะได้

ถ้าการเคลื่อนที่เกิดจากการขว้างวัตถุจากพื้นราบ และวัตถุตกลงมายังพื้นราบเดิม ก็จะได้ระยะทางในแนวดิ่ง หรือ s_y เป็นศูนย์

จะทำให้ได้เวลาที่ใช้ในการเคลื่อนที่เป็น

สำหรับการเคลื่อนที่ในแนวราบ หากถือว่าไม่มีแรงภายนอกในแนวราบมากระทำ และให้ s_x เป็นระยะทางของการเคลื่อนที่ในแนวราบนี้ จะได้

s_x = (ucosθ ) t

จัดรูปสมการใหม่ จะได้

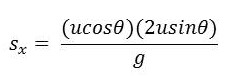
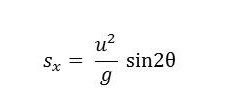
จากสมการข้างต้นจะเห็นว่า สำหรับอัตราเร็วต้นค่าหนึ่ง ๆ ระยะทางในแนวราบของวัตถุมีค่าขึ้นกับ sin2θ โดยค่าสูงสุดของระยะทางในแนวราบคือ u²/g ซึ่งเกิดขึ้นเมื่อ

sin2 θ = 1

= sin90^o

หรือ 2θ = 90^o

θ = 45^o

นั่นคือ สำหรับอัตราเร็วต้นค่าหนึ่ง ๆ ถ้าทิศทางของความเร็วต้นทำมุม 45^o กับแนวราบจะได้การเคลื่อนที่แบบโพรเจกไทล์ที่มีระยะทางในแนวราบมากที่สุด ในทางกลับกัน ถ้าต้องการขว้างวัตถุให้เคลื่อนที่แบบโพรเจกไทล์ และให้ระยะทางในแนวราบของวัตถุมีค่าหนึ่ง ความเร็วต้นที่น้อยที่สุดที่ใช้ในการขว้างวัตถุจะเกิดขึ้นเมื่อทิศทางของความเร็วต้นทำมุม 45^oกับแนวราบ

ดังนั้นจึงสรุปเกี่ยวกับการเคลื่อนที่แบบโพรเจกไทล์ได้ว่า

1) แนวระดับ ความเร็วคงตัว ความเร่งเท่ากับศูนย์

2) แนวดิ่ง ความเร็วไม่คงตัว ความเร่งคงตัวเท่ากับ g

3) แนวโค้งโพรเจกไทล์ ความเร็วไม่คงตัว (คิดแนวระดับ + แนวดิ่ง)

4) ทั้งแนวระดับ และแนวดิ่ง ใช้เวลาในการเคลื่อนที่เท่ากัน

5) ที่จุดสูงสุด อัตราเร็วหรือความเร็ว จะเท่ากับอัตราเร็ว หรือความเร็วของแนวระดับ เพราะของแนวดิ่งเท่ากับศูนย์

6) เมื่อกล่าวถึงอัตราเร็วหรือความเร็วจะหมายถึงอัตราเร็ว หรือความเร็วในแนวโค้งโพรเจกไทล์ ซึ่งเป็นผลจากการคิดรวมแนวระดับแนวดิ่งเข้าด้วยกัน

7) วัตถุเคลื่อนที่แบบโพรเจกไทล์ มีแรงดึงดูดของโลกเพียงแรงเดียวเท่านั้นที่กระทำกับวัตถุ

จากสมการ

8) ถ้า u คงที่ ค่า s_x จะมากที่สุดเมื่อ sin2θ มีค่ามากที่สุดนั่นคือ sin2θ = 1

9) ถ้า s_x คงที่ ค่า u จะน้อยที่สุดเมื่อ θ = 45^oด้วยเช่นกัน

10) ถ้า u คงที่ ค่า s_x จะเท่ากันสำหรับทกมุม θ คู่ใด ๆ ที่บวกกันได้ = 90^o เช่น 30^o กับ 60^o ได้ sin 30^ocos 30^o = sin 60^ocos 60^o, 37^o กับ 53^o ได้ sin 37^ocos 37^o = sin 53^ocos 53^o