ความสัมพันธ์และฟังก์ชัน
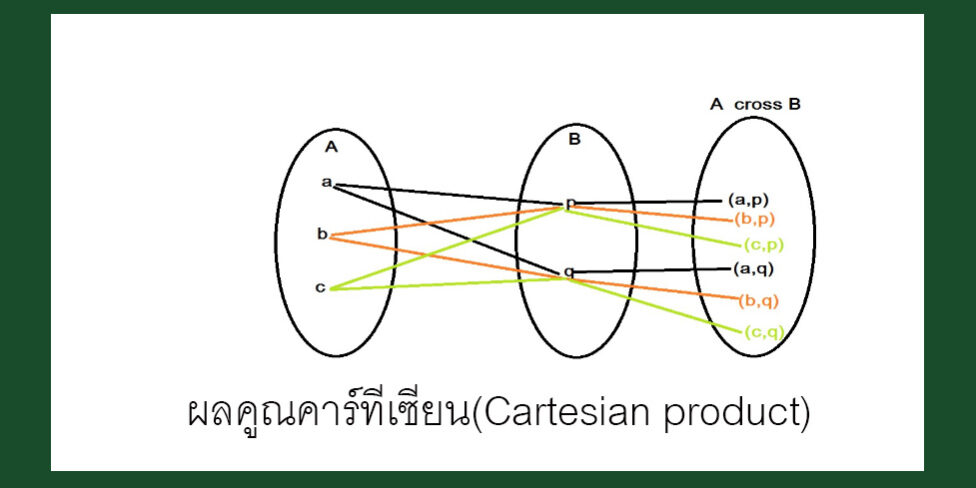
- ผลคูณคาร์ทีเชียน(Cartesian Product)
นิยาม คูณคาร์ทีเชียน ของเซต A และ B คือ เซตคู่ลำดับ (a,b) ทั้งหมดโดยที่ a Î A และ b Î B เช่น A = { 1,2,3} , B = {4,5,6}
และ A x B คือ ผลคูณคาร์ทีเชียนของเซต A และ เซต B ดังนั้น
A x B = {(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5),( 3,6)}
- ความสัมพันธ์ (Relation) หมายถึง เซตของคู่ลำดับ
2.1 ความสัมพันธ์จะมีขึ้นต้องมีเซตของคู่ลำดับ(Order Pairs) ก่อน
2.2 คู่ลำดับจะเกิดขึ้นได้เมื่อมี A x B หรือ B x A ซึ่งเป็นผลคูณคาร์ทีเชียนนั่นเอง
- โดเมน และ เรนจ์ของความสัมพันธ์ (Domain and Range of Relations)
ถ้ากำหนด R เป็นความสัมพันธ์
โดเมนของ R : (Dr) คือ เซตของสมาชิกตัวหน้าของคู่ลำดับ
เรนจ์ ของ R : (Rr) คือ เซตของสมาชิกตัวหลังของคู่ลำดับ
ผลคูณคาร์ทีเซียน (Cartesion product)
ผลคูณคาร์ทีเซียน ของ เซท A และ B คือ
เซตของคู่อันดับ ที่มีสมาชิกตัวหน้าเป็นเซตของ A
และสมาชิกตัวหลังเป็นเซตของ B
เขียน แทนด้วยภาษาคณิตศาสตร์เพื่อความเข้าใจที่ตรงกันคือ
ผลคูณคาร์ทีเซียน (Cartesion product)
เขียนแทนด้วย A X B อ่านว่า เอ คูณ บี หรือ เอ ครอส ( cross) บี
และเมื่อ B เป็นเซตว่าง จะทำให้ ค่า A X B เท่ากับเซตว่าง
ผลคูณคาร์ทีเซียน (Cartesion product)
สรุป อย่างภาษาง่าย ๆเราจะได้ ว่า เซต A คูณ เซต B
จะได้คู่อันดับ ซึ่งมีสมาชิกตัวแรกเป็นสมาชิก จากเซต A
และสมาชิกตัวที่สอง เป็นสมาชิก จากเซต B
ตัวอย่างผลคูณคาร์ทีเซียน
ตัวอย่างที่ 1 กำหนดให้ A = {4 , 5 } และ B = { 6, 7, 8}
จงหา A X B , B X A , A X A , B X B
วิธีทำ
1. หา A X B
” จะได้คู่อันดับซึ่ง นำสมาชิกของ A มาเป็นสมาชิกตัวแรก
และ นำสมาชิกจาก B มาเป็นตัวที่สอง “
ดังนั้น A X B = { (4,6), (4,7), (4,8), (5,6), (5,7), (5,8) }
B X A = { (6,4), (6,5), (7,4), (7,5), (8,4), (8,5) }
A X A = { (4,4), (4,5), (5,4), (5,5) }
A cross A
B X B={(6,6), (6,7), (6,8) , (7,6),
(7,7) , (7,8), (8,6),(8,7) ,(8,8) }
ตัวอย่างผลคูณคาร์ทีเซียน
ตัวอย่างที่ 2 กำหนดให้ A = {4 , 5 } ,B = { 4,5, 6}
และ C = { 5,8}
ตัวอย่างที่ 3
กำหนดให้ A = { 12,18 } , B = {Ø }
หา A X B
วิธีทำ เนื่องจาก B เท่ากับ เซตว่าง ดังนั้น ค่า ของ A X B = Ø
ตัวอย่างที่ 4
กำหนดให้ A ={1 ,2 } B = {P , Q ,R}
หา A X B โดยใช้ แผนภาพต้นไม้
วิธีทำ
แผนภูมิต้นไม้
A X B = { (1,P), (1,Q), (1,R), (2,P), (2,Q), (2,R) }
ตัวอย่าง R = {(-1,1),(0,0)}
โดเมน คือ {-1,0} เรนจ์ คือ {1,0}
- ฟังก์ชัน (Function) คือ ความสัมพันธ์อย่างหนึ่งโดยที่คู่ลำดับใด ๆ จะมี
สมาชิกตัวหน้าซ้ำกันไม่ได้
เช่น R1 = {(1,2),(1,4)} R1 ไม่เป็นฟังก์ชันเพราะสมาชิกตัวหน้าซ้ำกัน
R2 = {(1,3),(2,3)} R2 เป็นฟังก์ชัน ตามนิยาม
R3 = {(1,4),(2,3)} R3 เป็นฟังก์ชัน ตามนิยาม
- การตรวจสอบความสัมพันธ์ใดเป็นฟังก์ชันหรือไม่
- ลากเส้นขนานกับแกน y ตัดกราฟความสัมพันธ์ ได้ 1 จุดเป็นฟังก์ชันแต่ถ้าตัดกราฟเกิน 1 จุด ไม่เป็นฟังก์ชัน
- ตรวจสอบใช้หลักที่ว่า กำหนดให้ (a , b) Î r และ (a , c) Îr
เราสามารถสรุปได้ว่า b = c ก็แสดงว่าความสัมพันธ์เป็นฟังก์ชัน
ตัวอย่าง
จงตรวจสอบว่า r = {(x,y) ÎR x R y2 = 4x + 1 } เป็นฟังก์ชันหรือไม่
วิธีทำ
ใช้วิธีที่ 2 จาก y2 = 4x + 1
ให้ (a,b) Î r จะได้ b2 = 4a + 1 ——-(1)
ให้ (a,c) Î r จะได้ c2 = 4a + 1 ——–(2)
จาก (1) และ (2) จะได้ b2 = c2
b = ± c
เราไม่สามารถสรุปได้ว่า b = c แสดงว่าความสัมพันธ์นี้ไม่เป็นฟังก์ชัน
- ฟังก์ชันจาก A ไป B ถ้ากำหนดให้ f เป็นฟังก์ชันจาก A ไป B
มีเงื่อนไข Df = A
- ฟังก์ชัน 1 – 1 ( One – to – one function )
เป็นฟังก์ชันแบบ 1 – 1 ก็ต่อเมื่อ สมาชิกในเรนจ์แต่ละตัวมีความสัมพันธ์
กับสมาชิกในโดเมนเพียงตัวเดียวเท่านั้น
การตรวจสอบว่าเป็นฟังก์ชัน แบบ 1-1 หรือไม่ โดย
- ลากเส้นขนานกับแนวแกนx ตัดกราฟฟังก์ชัน 1 จุด เป็นฟังก์ชัน 1-1
ถ้าตัดกราฟฟังก์ชันมากกว่า 1 จุด ไม่เป็นฟังก์ชัน 1-1
- ตรวจสอบใช้หลักที่ว่า กำหนดให้ (a , c) Î f และ (b , c) Îf
เราสามารถสรุปได้ว่า a = b ก็แสดงว่าความสัมพันธ์เป็นฟังก์ชันแบบ1-1
- ฟังก์ชันไปทั่วถึง(onto function)
ถ้า f เป็นฟังก์ชันจาก A ไป B จะเรียก f ว่าเป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ Rf = B
- พีชคณิตของฟังก์ชัน คือ การนำฟังก์ชันมา บวก ลบ คูณ และหารกัน
- อินเวอร์สของฟังก์ชัน (f-1)
ถ้า r เป็นความสัมพันธ์จาก A ไป B อินเวอร์สของ r เขียนแทนด้วย r-1 ก็จะเป็นความสัมพันธ์จาก B ไป A
r = {(x,y) xÎA, yÎB } r-1 = {(y,x) (x,y)Îr }
การหาอินเวอร์สฟังก์ชัน(f-1)
(1) ที่ใดมี x แทนด้วย y และที่ใดมี y แทนด้วย x
(2) พยายามทำให้อยู่ในรูป y = f(x)
(3) y ตัวนี้คือ f-1 นั่นเอง
กรณีเขียนเป็นรูปคู่อันดับ การหาอินเวอร์สฟังก์ชัน(f-1) ทำได้โดย
ถ้า f = {(a,1),(b,2),(c,3)}
ดังนั้น f-1 = {(1,a),(2,b),(3,c)}
11.ฟังก์ชันคอมโพสิท(composite function) เป็นการกระทำตั้งแต่ฟังก์ชัน 2
ฟังก์ชันขึ้นไป โดยมีลักษณะเหมือนกับการนำฟังก์ชันนั้นมาเชื่อมกัน
ให้ f เป็นฟังก์ชันจาก A ไป B
ให้ g เป็นฟังก์ชันจาก B ไป C
เราสามารถสร้างฟังก์ชันจาก A ไป C ได้โดยเขียนแทนด้วย gof(x) = gf(x)
จะสร้าง gof(x) ได้ก็ต่อเมื่อ เรนจ์ของ f ต้องเป็นสับเซตของโดเมน g
ทดสอบความเข้าใจ
ข้อ 1. จงบอกโดเมน และเรนจ์ของความสัมพันธ์ R ต่อไปนี้
1.1) R1 = {(-3,9),(-2,4),(-1,1),(0,0),(1,1)}
เฉลย
ข้อ 1. โดเมนข้อ R1 = {-3,-2,-1,0,1}เรนจ์ R1 = {9,4,1,0,1}
เรนจ์ R5 = {Y Y Î R และ Y2 < 1 }