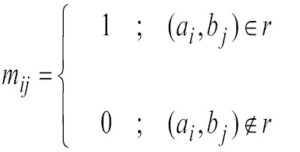ความสัมพันธ์และฟังก์ชัน(Relations and Functions)
คู่อันดับ
คู่อันดับประกอบด้วยสมาชิกสองตัว เขียนแทนคู่อันดับในรูป (a,b) โดยที่ a เป็นสมาชิกตัว
หน้า และ b เป็นสมาชิกตัวหลัง
การสลับที่กันของคู่อันดับระหว่างสมาชิกตัวหน้ากับสมาชิกตัวหลัง (a,b) (b,a) จะท าให้
ความหมายของคู่อันดับเกิดการเปลี่ยนทันที ดังนั้น จึงสามารถสรุปหลักการของคู่อันดับได้ ดังนี้
1. ถ้า (a,b) = (b,a) ก็ต่อเมื่อ a=b
2. ถ้า (a,b) = (c,d) ก็ต่อเมื่อ a=c และ b=d
3. ถ้า (a,b) (c,d) ก็ต่อเมื่อ a c หรือ b d
ผลค ูณคาร์ทีเชียน
ผลคูณคาร์ทีเชียนของเซต A และ B คือ เซตของคู่อันดับ (a,b) ที่มีสมาชิกตัวหน้าเป็น
เซตของ A และสมาชิกตัวหลังเป็นเซตของ B กล่าวคือ
AxB = {(a,b) | a∊A, b∊B}
สมบัติของผลค ูณคาร์ทีเชียล
ก าหนด A, B และ C เป็นเซตใดๆ
1. AxB BxA
2. Ax⏀=⏀xA=⏀
3. AxB=BxA ก็ต่อเมื่อ A=B หรือ A=⏀ หรือ B=⏀
4. Ax(B∪C)=(AxB)∪(AxC)
5. Ax(B∩C)=(AxB)∩(AxC)
6. Ax(B-C)=(AxB)-(AxC)
7. ถ้า A และ B เป็นเซตจ ากัดแล้ว n(AxB) = n(A) x n(B)
8. ถ้า A เป็นเซตอนันต์ และ B เป็นเซตจ ากัด ซึ่ง B 0 แล้ว AxB และ BxA เป็น
เซตอนันต์
Ex. กำหนด A={1,2,3} , B={a,b} จงหา AxB, BxA, AxA, BxB
AxB = ? ลองหาคำตอบ
BxA =? ลองหาคำตอบ
AxA = ? ลองหาคำตอบ
BxB = ? ลองหาคำตอบ
ถ้า A และ B เป็นเซตจ ากัด AxB จะมีจ านวนสมาชิกของ A คูณด้วยจ านวนสมาชิกของ
B เช่น ถ้าจ านวนสมาชิกของ A เท่ากับ 3 จ านวนสมาชิกของ B เท่ากับ 2 ดังนั้น จ านวนของ
สมาชิกของ AxB = 3×2 = 6
ความสัมพันธ์
– r เป็นความสัมพันธ์จากเซต A ไปเซต B ก็ต่อเมื่อ r⊂AxB
– r เป็นความสัมพันธ์ในเซต A ก็ต่อเมื่อ r⊂AxA
– จำนวนความสัมพันธ์จากเซต A ไปเซต B เท่ากับ 2
n(AxB)
– เป็นความสัมพันธ์จากเซต A ไปเซต B เนื่องจาก ⏀⊂AxB
Ex. ให้ A = {x | x เป็นจ านวนเฉพาะ} , B={x | x เป็นจ านวนเต็มบวก}
กำหนดให้ r1 และ r2
เป็นความสัมพันธ์จาก A ไป B
r1 = {(x,y) ∊ AxB | y=2x}
r2 = {(x,y) ∊ AxB | y=x2
พิจารณาความสัมพันธ์
r1 = {(1,2),(2,3),(3,4),(4,5)}
r2 = {(x,y) I+x I+ | y = x }
เซตสมาชิกตัวหน้าของความสัมพันธ์ r 1 คือ {1,2,3,4} เรียกเซตนี้ว่า โดเมนของ r1
เซตสมาชิกตัวหลังของความสัมพันธ์ r 1 คือ {2,3,4,5} เรียกเซตนี้ว่า เรนจ์ของ r1
ส่วน r2 มีโดเมนและเรนจ์เท่ากับจำนวนเต็มบวก
บทนิยาม ให้ r เป็นความสัมพันธ์จาก A ไป B
โดเมนของ r คือเซตของสมาชิกตัวหน้าของคู่อันดับใน r เขียนแทนด้วย Dr
เรนจ์ของ r คือเซตของสมาชิกตัวหลังของคู่อันดับใน r เขียนแทนด้วย R r
ตัวอย่างที่ 1 กำหนดให้ A = {-2,-1,0,1,2} , B = {1,2,3,4}
กำหนด r = {(x,y) A x B | y = x2+1} จะได้
r = {(-1,2),(0,1),(1,2)}
ดังนั้น D r = {-1,0,1} , R r = {2,1}
ตัวอย่างที่ 2 จงหา โดเมนและเรนจ์ ของ r เมื่อกำหนด r = {(x,y)| ![]() RxR | x+y = 5}
RxR | x+y = 5}
วิธีทำ หาโดเมน จัดรูป y ในเทอม x จะได้ y = 5 – x จะเห็นว่าเมื่อแทนค่า x ด้วยจำนวนจริงใดๆจะหาค่า y ได้เสมอ ดังนั้น โดเมนคือจำนวนจริง หรือ เขียนในรูปเงื่อนไขได้เป็น Dr = { x|x R }
หาเรนจ์ จัดรูป x ในเทอม y จะได้ x = 5 – y จะเห็นว่าเมื่อแทนค่า y ด้วยจำนวนจริงใดๆจะหาค่า x ได้เสมอ ดังนั้น เรนจ์คือจำนวนจริง หรือ เขียนในรูปเงื่อนไขได้เป็น R r = { x|x R }
บทสรุปความสัมพันธ์และฟังก์ชัน(Relations and Functions)
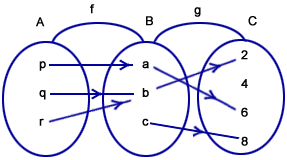
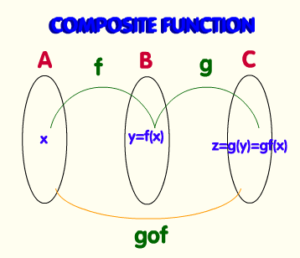
1. Composite Relations
คือ ความสัมพันธ์เชิงซ้อนระหว่างเซต
จากภาพจะเห็นว่าเซต f คือความสัมพันธ์ระหว่างเซต A
กับเซต B
และเซต g คือความสัมพันธ์เซต B กับเซต C
ซึ่งความสัมพันธ์ระหว่าง f กับ g จะได้ว่า fog
2. Properties of relations
a.Reflexive (∀∈,A(X,Y)∈r)
สมบัติสะท้อน ( Reflexive ) คือ สมาชิกทุกตัวของเซต A มีความสัมพันธ์กับตัวมันเอง (a ∈ A) และ (a,a) ∈ R
เช่น กำหนด A={1,2,3} และ R={(1,1), (1,2), (1,3), (3,3)}
S={(1,1), (1,2), (2,1), (2,2), (3,3)}
จะได้ว่า R ไม่มี refexive เพราะ 2 ϵ A แต่ (2,2) ∉ R
S มี refexive
b. Symmetric (∀(X,Y)∈,(Y,X)∈r)
สมบัติสมมาตร ( Symmetric ) คือ ความสัมพันธ์ R โดยที่ถ้า (a,b) ϵ R แล้ว (b,a) ϵ R
เช่น กำหนด A={1,2,3} และ R={(1,1), (1,2), (1,3), (3,3)}
S={(1,1), (1,2), (2,1), (2,2), (3,3)}
จะได้ว่า R ไม่มี symmetric เพราะ (1,2) ϵ R แต่ (2,1) ∉ R
S มี symmetric
c. Antisymmetric (∀(X,Y)∈r,(X,X)∈/r)
สมบัติปฏิสมมาตร (Antisymmetric) คือ ความสัมพันธ์ R โดยที่ถ้า (a,b) ϵ R แล้ว (b,a) ϵ R “และ a=b”
เช่น กำหนด A={1,2,3} และ R={(1,1), (1,2), (1,3), (3,3)}
S={(1,1), (1,2), (2,1), (2,2), (3,3)}
จะได้ว่า R เป็น Antisym
S ไม่เป็น Antisym เพราะ (1,2) และ (2,1) อยู่ใน S แต่ 1 ไม่เท่ากับ 2
d. Transitive (∀ (X,Y)^(X,Z)∈ r)
สมบัติถ่ายทอด ( Transitive ) คือ ความสัมพันธ์ R โดยที่ถ้า (a,b) ϵ R เเละ (b,c) ϵ R แล้ว (a,c) ϵ R
เช่น กำหนด A={1,2,3} และ R={(1,1), (1,2), (1,3), (3,3)}
S={(1,1), (1,2), (2,1), (2,2), (3,3)}
จะได้ว่า R และ S มี transitive
3. Combining properties
a.Equivalent
คือ เซตที่มีจำนวนสมาชิกเท่ากันแต่มีสมาชิกที่ไม่เหมือนกัน
เช่น กำหนดให้ A={1,2,3,4,5} , B ={a,b,c,d,e}
จะได้ว่า A equivalent B (Aเทียบเท่าB)
b.Partial order
c.Strict partial order
d.Total order
e.Strict total order
4. Representation of relations (2)
a.Matrix
การแทนค่าของความสัมพันธ์ในรูปแบบ Matrix (0-1) โดยกำหนดให้ R เป็นความสัมพันธ์จากเซต A = {a1, a2, … , an} ไป เซต B = {b1, b2, … , bn}
สามารถแทนด้วย matrix MR = [ mij ] โดยที่ …
เช่น กำหนด
ให้ A = { 1, 2, 3 } และ B = { 1, 2, 3, 4}
ให้ r เป็นความสัมพันธ์จาก A ไป B ซึ่ง r = {(a,b) ∈ AXB l a<b}
โดยจัดเป็นเมทริกซ์ได้ดังนี้…
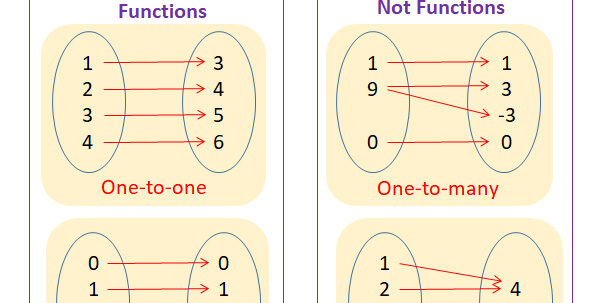
5. Functions
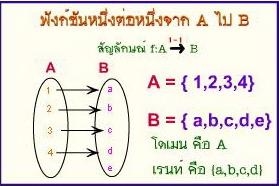
a.1-1 or Injection
ฟังก์ชันหนึ่งต่อหนึ่ง เป็นฟังก์ชั่นที่สมาชิกทุกตัวของเซต A มีความสัมพันธ์กับสมาชิกบ้างตัวในเซต B
โดยไม่ครบทั้งหมดในสมาชิกของเซต B
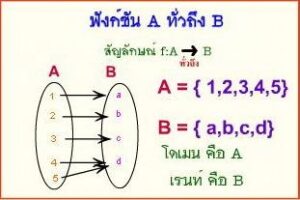
b.Onto or Surjection
ฟังก์ชั่นทั่วถึง เป็นฟังก์ชั่นที่สมาชิกทุกตัวของเซต A มีความสัมพันธ์กับสมาชิกทุกตัวในเซต B
โดยมีความสัมพันธ์ซ้ำกันได้
เช่น
c.1-1 onto or Bijection
ฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง เป็นฟังก์ชั่นที่สมาชิกทุกตัวของเซต A มีความสัมพันธ์กับสมาชิกทุกตัวในเซต B
โดยมีความสัมพันธ์ไม่ซ้ำกัน โดยมากมักใช้แสดงว่าเซต A และเซต B มีขนาดเท่ากัน
เช่น
d.Inverse
ฟังก์ชั่นผกผัน เป็นฟังก์ชันที่เกิดจากการนำคู่อันดับ(Ordered Pair)ในเซตมาสลับที่กัน
เช่น A = {(0,a),(1,b),(2,c),(3,d),(4,e)}
A^(-1) = {(a,0),(b,1),(c,2),(d,3),(e,4)}
6. Composite Function
ฟังก์ชั่นประกอบ คือ การแจกแจงสมาชิกจาก f ไป g
โดยที่ฟังก์ชั่นเป็นเซตแบบแจกแจง
นิยาม!! ให้ f และ g เป็นฟังก์ชัน และ Rf ∩ Dg ฟังก์ชันคอมโพสิทของ f และ g
เขียนแทนด้วย gof กำหนด (gof)(x) = g(f(x)) ซึ่ง f(x) ∈ Dg
gof (จีโอเอฟ)
เช่น กำหนด f = {(1,2),(3,4),(5,6),(7,8)} , g = {(2,a),(4,b),(7,c),(8,d)}
เนื่องจาก gof เป็นฟังก์ชัน จาก f ไป g
R f = {2,4,6,8} , Dg = {2,4,7,8}
R f ∩ Dg = {2,4,8} ≠ Ø แสดงว่าหา gof ได้
ดังนั้นจะได้ gof = {(1,a),(3,b),(7,d)}
ส่วน fog (เอฟโอจี)
fog เป็นฟังก์ชันจาก g ไป f
จากตัวอย่างข้างต้น…
Rg = {a,b,c,d} , Df = {1,3,5,7}
Rg ∩ Df = Ø
แสดงว่าหา fog ไม่ได้
RxR | x+y = 5}