ทฤษฎีกราฟเบื้องต้น
กราฟเป็นแบบจำลองทางคณิตศาสตร์ ซึ่งใช้จำลองปัญหาบางปัญหาโดยเขียนแผนภาพที่ประกอบด้วยจุดและเส้น ปัจจุบันมีการนำทฤษฎี
บทนิยาม กราฟ G ประกอบด้วยเซตจำนวน 2 เซต คือ
1. เซตที่ไม่เป็นเวตว่างของจุดยอด (vertex) แทนด้วยสัญลักษณ์ V(G)
2. เซตของเส้นเชื่อม (edge) ที่เชื่อมระหว่างจุดยอดแทนด้วยสัญลักษณ์ E(G)
2. ดีกรี
ดีกรีของจุดยอด
ต่อไปจะเรียกจำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอดว่า ดีกรี ใช้สัญลักษณ์ deg v แทนดีกรีของจุดยอด v ตัวอย่างที่ 1 กำหนดกราฟ ดังรูป
deg d = 4

จากทฤษฎีบท 1 ผลรวมของดีกรีของจุดยอดทุดจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ
ดังนั้น จำนวนจุดยอดทั้งหมดของกราฟ คือ 3 + 6 = 9 จุด
ดังนั้น เป็นไปไม่ได้ที่จะมีกราฟดังกล่าว
ตัวอย่างที่ 6 กำหนดกราฟ ดังรูป
ทฤษฎีบท2 ทุกกราฟจะมีจุดยอดคี่เป็นจำนวนคู่
จะได้ว่า กราฟมีจุดยอดคี่เป็นจำนวน 3 จุด ซึ่งขัดแย้งกับทฤษฎีบท 2 สรุปได้ว่า ไม่มีกราฟที่มีสมบัติดังกล่าว
จะได้ว่า กราฟนี้มีจุดยอด 23 จุด และจุดยอดแต่ละจุดมีดีกรี 7
อ
-
-
- เครือข่าย ที่แสดงเป็นกราฟจะประกอบด้วยจุดเชื่อมโยง (Vertices) และเส้นเชื่อมโยงระหว่างจุด เรียกว่า arcs
-
-
-
- จุด ที่มีจำนวนเส้นที่เชื่อมออกไปยังจุดอื่นเป็นจำนวนคี่ เรียกว่า odd และถ้าจุดนั้นมีเส้นเชื่อมออกไปยังจุดอื่นเป็นจำนวนคู่ จะเรียกว่า even
-
-
-
- เส้นทางออยเลอร์ คือเส้นทางที่ลากผ่านเส้นต่าง ๆ ในเครือข่าย โดยแต่ละเส้นลากผ่านได้เพียงครั้งเดียว
-
-
- ทฤษฎีของออยเลอร์ กล่าวว่า ถ้าหากว่าเครือข่ายใดมีจุดที่เป็น odd มากกว่าสองขึ้นไป จะไม่มีทางสร้างเส้นทางออยเลอร์ได้
ตัวอย่างจงพิจารณาว่ารูป A, B และ C เป็นกราฟหรือไม่ เพราะเหตุใด
A เป็นกราฟเนื่องจากเซตของจุดยอดไม่เป็นเซตว่าง
B ไม่เป็นกราฟเนื่องจากเซตของจุดยอดเป็นเซตว่าง
C เป็นกราฟเนื่องจากเซตของจุดยอดไม่เป็นเซตว่าง
ตัวอย่างกำหนดกราฟ G1และ G2ดังรูป จงหาเซตของจุดยอด และเส้นเชื่อมของกราฟ จากกราฟที่กำหนดให้
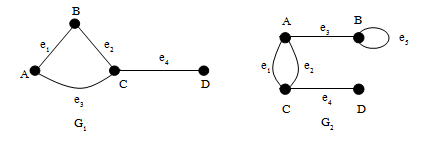
จากกราฟ G1ที่กำหนดให้ จะได้ว่า
V(G1) = {A, B, C, D}
E(G1) = {e1, e2, e3, e4} = {AB, BC, AC, CD}
จากกราฟ G2ที่กำหนดให้ จะได้ว่า
V(G2) = {A, B, C, D}
E(G2) = { e1, e2, e3, e4, e5}
จากกราฟ G2ของตัวอย่างที่ 2 จะสังเกตเห็นได้ว่า เส้นเชื่อม e1และ e2เป็นเส้นเชื่อมที่เชื่อมระหว่างจุดยอดคู่เดียวกัน คือ จุดยอด A และ C หากเราเรียกเส้นเชื่อม e1และ e2โดยอาศัยจุดยอดของเส้นเชื่อม จะพบว่าทั้งเส้นเชื่อม e1และ e2มีชื่อ AC เหมือนกัน ทำให้ไม่สามารถแยกเส้นเชื่อมทั้งสองออกจากกันได้ จึงสรุปได้ว่า การเรียกชื่อเส้นเชื่อมจากจุดยอดทั้งสองของเส้นเชื่อมนั้น ทำได้ในกรณีที่ระหว่างจุดยอดทั้งสองมีเส้นเชื่อมเพียงเส้นเดียวเท่านั้น
บทนิยามจุดยอด u และ v ของกราฟเป็นจุดยอดประชิด(Adjacent Vertices) ก็ต่อเมื่อ มีเส้นเชื่อมระหว่างจุดทั้งสอง และเราเรียกจุดยอด u และ v ว่าจุดปลาย(End Point) ของเส้นเชื่อมนั้น
เส้นเชื่อม e ของกราฟเกิดกับ(Incident) จุดยอด v ถ้าจุดยอด v เป็นจุดปลายจุดหนึ่งของเส้นเชื่อม e
ตัวอย่างจงแสดงว่าจุดยอดใดเป็นจุดยอดประชิด และเส้นเชื่อมแต่ละเส้นเชื่อมเกิดกับจุดยอดใด
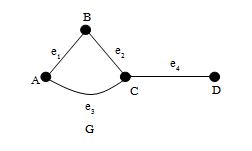
จุดยอด A และจุดยอด B เป็นจุดยอดประชิด
จุดยอด A และจุดยอด C เป็นจุดยอดประชิด
จุดยอด A และจุดยอด D ไม่เป็นจุดยอดประชิด
จุดยอด B และจุดยอด C เป็นจุดยอดประชิด
จุดยอด B และจุดยอด D ไม่เป็นจุดยอดประชิด
จุดยอด C และจุดยอด D เป็นจุดยอดประชิด
เส้นเชื่อม e1เกิดกับ จุดยอด A และ จุดยอด B
เส้นเชื่อม e2เกิดกับ จุดยอด B และ จุดยอด C
เส้นเชื่อม e3เกิดกับ จุดยอด A และ จุดยอด C
เส้นเชื่อม e4เกิดกับ จุดยอด C และ จุดยอด D
บทนิยามเส้นเชื่อมตั้งแต่ 2 เส้นเชื่อมที่เชื่อมระหว่างจุดยอดคู่เดียวกัน เรียกว่าเส้นเชื่อมขนาน(Parallel Edges)
เส้นเชื่อมที่เชื่อมจุดยอดเพียงจุดเดียว เรียกว่าวงวน(Loop)
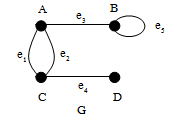
จากภาพจะพบว่า เส้นเชื่อม e1และ e2เชื่อมระหว่างจุดยอดคู่เดียวกัน คือ จุดยอด A และ C ดังนั้นจะได้ว่า e1และ e2เป็นเส้นเชื่อมขนานที่เกิดกับจุดยอด A และ C นอกจากนี้จะพบอีกว่า e5เป็นเส้นเชื่อมที่เชื่อมจุดยอด B เพียงจุดเดียว จึงเรียก e5ว่า วงวน
หมายเหตุ
Ü ในการเขียนแผนภาพของกราฟนั้น จะกำหนดตำแหน่งของจุดยอด ณ ตำแหน่งใดก็ได้ และจะลากเส้นเชื่อมของกราฟเป็นเส้นตรง หรือเส้นโค้ง มีความยาวเป็นเท่าใดก็ได้ โดยที่เส้นเชื่อมที่ลากจะไม่ตัดกับตัวมันเอง และไม่ลากผ่านจุดยอดที่ไม่ใช่จุดปลายของเส้นเชื่อมนั้น เช่น กราฟ G1และ G2ถือว่าเป็นกราฟเดียวกัน
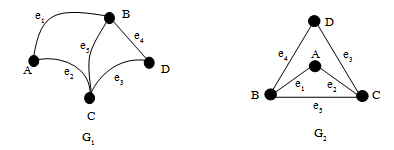
Ü เส้นเชื่อมสองเส้นของกราฟ อาจลากตัดกันได้ โดยที่จุดตัดของเส้นเชื่อมทั้งสองไม่ถือว่าเป็นจุดยอดของกราฟ เช่น กราฟ G3และ G4ถือว่าเป็นกราฟเดียวกัน

-ขอบคุฯแหล่งข้อมูล http://mathematics-pr.blogspot.com/p/blog-page_4945.html
และ https://www.scimath.org/lesson-mathematics/item/7334-2017-06-17-14-37-32












