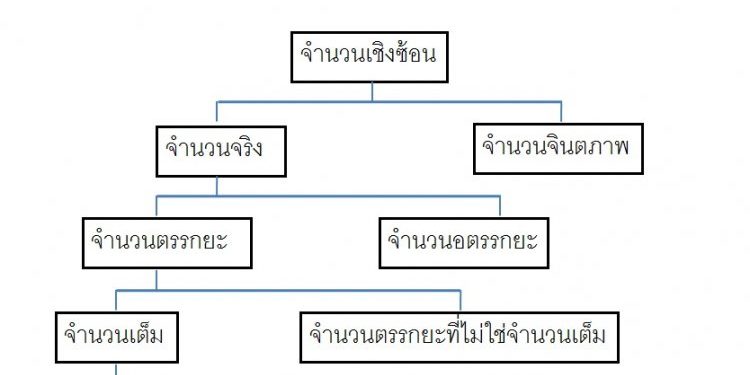
จำนวนจริงประกอบด้วย จำนวนอตรรกยะ และ จำนวนตรรกยะ ซึ่งเราจะพิจารณาในรายละเอียดได้ดังนี้
- จำนวนอตรรกยะ คือ จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือ ทศนิยมซ้ำได้ ยกตัวอย่างเช่น√2, √3,√5 หรือค่า¶ เป็นต้น
- จำนวนตรรกยะ คือ จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือ ทศนิยมซ้ำได้ยกตัวอย่างเช่น 1/2, 1/3, 2/5 เป็นต้น
จากแผนภาพอีกเช่นเคย จะเห็นได้ว่า จำนวนตรรกยะ จะประกอบด้วยสองส่วนคือ จำนวนเต็ม และ จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม
- จำนวนเต็ม คือจำนวนที่เป็นตัวเลขเต็มๆ หรือ ตัวเลขที่ไม่มีทศนิยมนั่นเอง นั่นคือ ตัวเลขที่เราใช้นับนั่นเอง ยกตัวอย่างเช่น 1, 2, 3, 4 … ทั้งนี้ทั้งนั้น รวมไปจนถึงค่าที่ติบลบของจำนวนนับนี้และศูนย์ด้วย เช่น 0, -1, -2, -3, -4 ….
- จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม ความหมายของจำนวนนี้ก็ตามความหมายของชื่อเลยครับ นั่นคือ ตัวเลขเขียนในรูปของทศนิยมซ้ำได้โดยที่ไม่ได้เป็นเลขจำนวนเต็มนั่นเอง อย่างเช่น 1/2=0.5 หรือ 1/3 = 0.333… (สามซ้ำ)
ยิ่งไปกว่านั้น จำนวนเต็มยังแบ่งย่อยได้อีกสามหมวดคือ จำนวนเต็มลบ จำนวนเต็มบวก และ จำนวนเต็มศูนย์
สมบัติของจำนวนจริง
เนื่องจากว่า สมบัติของจำนวนจริงมีเยอะมาก ในที่นี้จะนำเสนอเฉพาะที่คิดว่าสำคัญแล้วกันนะครับ
ถ้าให้ a, b และ c เป็นจำนวนจริงใดๆ แล้ว จะได้ว่าจำนวนจริงจะมีสมบัติดังต่อไปนี้
1. สมบัติปิดการบวก: a+ b จะต้องเป็นจำนวนจริงเสมอ
2. สมบัติการเปลี่ยนหมู่ของการบวก: a + (b + c) = (a + b) + c
3. สมบัติการมีเอกลักษณ์การบวก: a + 0 = a = 0 + a โดยที่เราเรียก 0 ว่าเอกลักษณ์ของการบวก
4. สมบัติการมีอินเวอร์สของการบวก: a + (-a) = 0 = (-a) + a โดยที่ (-a) เป็นอินเวอร์สการบวกของ a
5. สมบัติปิดของการคูณ: a คูณ b หรือ ab จะต้องมีผลลัพธ์เป็นจำนวนจริงเสมอ
6. สมบัติการเปลี่ยนหมู่ของการคูณ: a(bc) = (ab) c
7. สมบัติการมีเอกลักษณ์การคูณ: a x 1 = a = 1 x a โดยที่เราเรียก 1 ว่าเอกลักษณ์ของการคูณ
8. สมบัติการมีอินเวอร์สของการคูณ: a a-1 = 0 = a-1 a โดยที่ a-1 เป็นอินเวอร์สการคูณของ a
9. สมบัติการแจกแจงทางซ้าย: a(b + c) = ab + ac
นอกจากสมบัติของจำนวนจริงแล้ว เรายังมีทฤษฎีบทเบื้องต้นสำหรับจำนวนจริงด้วย ในทำนองเดียวกับสมบัติของจำนวนจริง จะขอนำเสนอเฉพาะส่วนที่คิดว่าสำคัญเท่านั้นนะครับ
ถ้าให้ a, b, c และ d เป็นจำนวนจริงใดๆ จะได้ว่า
1. ถ้า a+c = b+c แล้ว a = b
2. ถ้า c ไม่เท่ากับศูนย์ และ ac =ab แล้ว a = b
3. เมื่อ c > 0 แล้วจะได้ว่า
(1) ถ้า a > b แล้ว ac > bc
(2) ถ้า a < b แล้ว ac < bc
(3) ถ้า ac > bc แล้ว a > b
(4) ถ้า ac < bc แล้ว a < b
4. เมื่อ c < 0 แล้วจะได้ว่า
(1) ถ้า a > b แล้ว ac < bc
(2) ถ้า a < b แล้ว ac > bc
(3) ถ้า ac > bc แล้ว a < b
(4) ถ้า ac < bc แล้ว a > b
5. ถ้า ab = 0 แล้ว a = 0 หรือ b = 0
6. ถ้า a < b และ c < d แล้ว a – d < b – c
สมบัติการเท่ากันของจำนวนจริง
กำหนด a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติการสะท้อน a = a
2. สมบัติการสมมาตร ถ้า a = b แล้ว b = a
3. สมบัติการถ่ายทอด ถ้า a = b และ b = c แล้ว a = c
4. สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว a + c = b + c
5. สมบัติการคูณด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว ac = bc
สมบัติการบวกในระบบจำนวนจริง
กำหนด a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติปิดการบวก a + b เป็นจำนวนจริง
2. สมบัติการสลับที่ของการบวก a + b = b + c
3. สมบัติการเปลี่ยนกลุ่มการบวก a + ( b + c) = ( a + b ) + c
4. เอกลักษณ์การบวก 0 + a = a = a + 0
นั่นคือ ในระบบจำนวนจริงจะมี 0 เป็นเอกลักษณ์การบวก
5. อินเวอร์สการบวก a + ( -a ) = 0 = ( –a ) + a
นั่นคือ ในระบบจำนวนจริง จำนวน a จะมี –a เป็นอินเวอร์สของการบวก
สมบัติการคูณในระบบจำนวนจริง
กำหนดให้ a, b, c, เป็นจำนวนจริงใดๆ
1. สมบัติปิดการคูณ ab เป็นจำนวนจริง
2. สมบัติการสลับที่ของการคูณ ab = ba
3. สมบัติการเปลี่ยนกลุ่มของการคูณ a(bc) = (ab)c
4. เอกลักษณ์การคูณ 1 · a = a = a · 1
นั่นคือในระบบจำนวนจริง มี 1 เป็นเอกลักษณ์การคูณ
5. อินเวอร์สการคูณ a · a-1 = 1 = a · a-1, a ≠ 0
นั่นคือ ในระบบจำนวนจริง จำนวนจริง a จะมี a-1 เป็นอินเวอร์สการคูณ ยกเว้น 0
6. สมบัติการแจกแจง
a( b + c ) = ab + ac
( b + c )a = ba + ca
แหล่งข้อมูล https://www.scimath.org/lesson-mathematics/item/7058-2017-05-24-14-59-48