สมบัติของฟังก์ชันเอกซ์โพเนนเชียล
สมบัติที่สำคัญของฟังก์ชันเอกซ์โพเนนเชียล
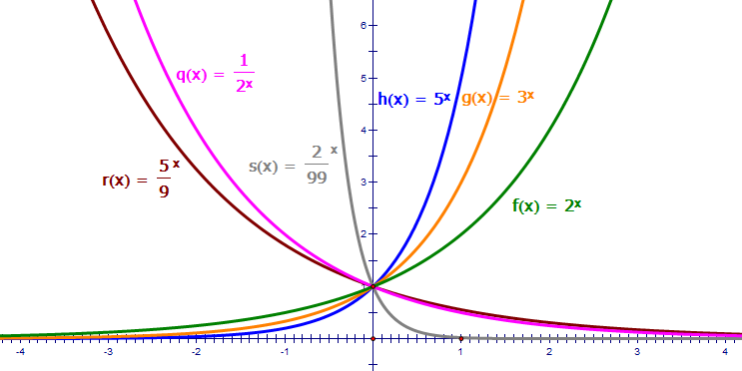
- เมื่อ a > 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันเพิ่ม และเมื่อ 0 < a < 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันลด
- ไม่มีค่าสูงสุดและค่าต่ำสุดของฟังก์ชัน
- กราฟของฟังก์ชันจะผ่านจุด (0, 1) และจะอยู่เหนือแกน X เสมอ
- โดเมนของฟังก์ชันเป็นจำนวนจริง (R) และเรนจ์ของฟังก์ชันเป็นจำนวนจริงบวก
- เมื่อ a มีค่ามาก ๆ กราฟของฟังก์ชันจะเรียวยาว
- แกน y จะเป็นแกนสมมาตรของกราฟของฟังก์ชัน y = ax และ y = (1/2)x
- กราฟของฟังก์ชันเอกซ์โพเนนเชียลบนระนาบ X’Y’ มีจุดกำเนิดที่ (h,k) เทียบกับระนาบ XY มีจุดกำเนิดที่ (0, 0) จะมีสมการเป็น y- k = ax-h
- ax = ay ก็ต่อเมื่อ x = y
- ถ้า ax > ay แล้ว x > y เมื่อ a > 1
- ถ้า ax > ay แล้ว x < y เมื่อ 0 < a < 1
ฟังก์ชันชี้กำลังที่สำคัญถูกนำมาใช้ในศาสตร์อย่างหลากหลาย ได้แก่ฟังก์ชัน
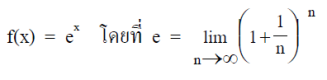
ฟังก์ชันเอกซ์โพเนนเชียล
เลขยกกำลัง
1. เลขยกกำลัง คือจำนวนที่เขียนในรูป an โดยเรียก a ว่าฐาน และเรียก n ว่า เลขชี้กำลัง (Exponent) ซึ่งถ้าเลขชี้กำลัง n เป็นจำนวนนับ แล้ว an จะแทน a คูณกันเป็นจำนวน n ตัว หรือ
an=a∙a∙a∙… ∙a (n ตัว)
แต่ถ้าเลขชี้กำลังเป็นศูนย์ หรือจำนวนลบ หรือเศษส่วน จะเป็นไปตามนิยามดังนี้
a0=1, a-n=1an(โดยที่ a≠0)และ a1n=na
2. สมบัติของเลขยกกำลัง
กำหนดให้ a , b เป็นจำนวนจริงใด ๆ
|
1. am∙an=am+n |
6. (ab)n=anbn |
|
2. . aman=am-n |
7. nab=na∙nb |
|
3 (am)n=amn |
8. nab=nanb |
|
4. nam=amn |
9. am=an ก็ต่อเมื่อ m=n |
|
5. (ab)n=an∙bn |
10. am=bm ก็ต่อเมื่อ a=b หรือ m=0 |
สมบัติที่สำคัญของฟังก์ชันเอกซ์โพเนนเชียล
1. เมื่อ a > 1 ฟังก์ชัน y=ax จะเป็นฟังก์ชันเพิ่ม และเมื่อ 0 < a < 1 ฟังก์ชัน y=ax จะเป็นฟังก์ชันลด
2. ไม่มีค่าสูงสุดและค่าต่ำสุดของฟังก์ชัน
3. กราฟของฟังก์ชันจะผ่านจุด (0, 1) และจะอยู่เหนือแกน X เสมอ
4. โดเมนของฟังก์ชันเป็นจำนวนจริง (R) และเรนจ์ของฟังก์ชันเป็นจำนวนจริงบวก ( R+)
5. เมื่อ a มีค่ามาก ๆ กราฟของฟังก์ชันจะเรียวยาว
6. แกน y จะเป็นแกนสมมาตรของกราฟของฟังก์ชัน y = ax และ y=(1a)x
7. กราฟของฟังก์ชันเอกซ์โพเนนเชียลบนระนาบ X ‘Y ‘ มีจุดกำเนิดที่ ( h, k) เทียบกับระนาบ XY มีจุดกำเนิดที่ (0, 0) จะมีสมการเป็น y – k = ax-h
8. a x= ay ก็ต่อเมื่อ x =y
9. ถ้า a x> ay แล้วx> y เมื่อ a > 1
10. ถ้า a x> ay แล้ว x < y เมื่อ 0 < a < 1
ฟังก์ชัน
1.ฟังก์ชัน (Function) คือ ความสัมพันธ์ ซึ่งในสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น ถ้ามีสมาชิกตัวหน้าเท่ากันแล้ว สมาชิกตัวหลังต้องไม่แตกต่างกัน
หรือ
ฟังก์ชัน คือ ความสัมพันธ์ ซึ่งในสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น ถ้าสมาชิกตัวหน้าเท่ากัน สมาชิกตัวหลังต้องเท่ากันด้วย
นั่นคือ ความสัมพันธ์ f จะเป็นฟังก์ชัน ก็ต่อเมื่อ ถ้า (x, y1) ε f และ (x, y2) ε f แล้ว y1 = y2
ถ้าหากว่าความสัมพันธ์ที่กำหนดให้อยู่ในรูปแบบบอกเงื่อนไข การตรวจสอบว่าความสัมพันธ์นั้นเป็นฟังก์ชันหรือไม่สามารถทำได้กลายวิธี
คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง
(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d
ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B
สัญลักษณ์ ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x B
หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า
![]()
ความสัมพันธ์ (Relation)
เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A x B
โดเมน (Domain) และ เรนจ์ (พิสัย) (Range)
- โดเมน (Domain) ของความสัมพันธ์ r คือ เซตที่มีสมาชิกตัวหน้าของทุกคู่อันดับในความสัมพันธ์ r ใช้สัญลักษณ์แทนด้วย Dr ดังนั้น Dr = {x | (x, y) ε r}
- เรนจ์ (Range) ของความสัมพันธ์ r คือ เซตที่มีสมาชิกตัวหลังของทุกคู่อันดับในความสัมพันธ์ r ใช้สัญลักษณ์แทนด้วย R rดังนั้น Rr = {y | (x, y) ε r}