สับเซต และ เพาเวอร์เซต

            สับเซต (subset) หรือ “เซตย่อย”  คือ เซตที่เล็กกว่าหรือเท่ากันกับเซตที่กำหนด โดยต้องใช้สมาชิกร่วมกับเซตที่กำหนดเท่านั้น

            สัญลักษณ์ที่ใช้แทนประโยค “ A เป็นสับเซตของ B” คือ A Ì B และจะเกิดขึ้นได้ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A นั้นเป็นสมาชิกของเซต B ด้วย หรือเมื่อ A เป็นเซตว่างก็ได้

เช่น {1,2}Ì{1,2,3}เนื่องจากทั้ง 1 และ 2 เป็นสมาชิกของ {1,2,3}

รูปแบบ เซต (เล็ก) Ì เซต(ใหญ่)

สมบัติของซับเซต

1. A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2. A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3. Ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4. ถ้า A ⊂ ø แล้ว A = ø

5. ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6. A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7. ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

การหาสับเซตทั้งหมดของA

จำนวนสับเซตทั้งหมดหาได้จาก 2ⁿ เมื่อ n = จำนวนสมาชิกในเซต

ตัวอย่าง             จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}

A จะมีสับเซตทั้งหมด 2⁴ =16 สับเซต เมื่อแจกแจงสับเซตทั้งหมดจะได้ดังนี้

Ø

{2}  {4}  {6}  {8}

{2, 4}  {2, 6}  {2, 8}  {4, 6}  {4, 8}  {6, 8}

{2, 4, 6}  {2, 6, 8}  {2, 4, 8}  {4, 6, 8}

{2, 4, 6, 8}

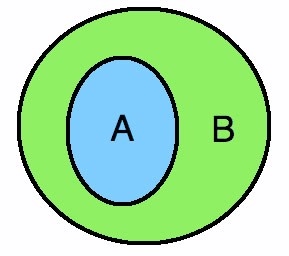
ความหมายของสับเซตแท้

สับเซตแท้ คือ สับเซตทั้งหมดที่ไม่ใช่ตัวมันเอง มี 2ⁿ – 1 สับเซต (เซตว่างไม่มีสับเซตแท้)

นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B

ซึ่งจะได้รูปดังภาพ

การหาจำนวนสับเซตทั้งหมดของ A

            หลักในการเขียนสับเซตทั้งหมดของเซตๆหนึ่งที่โจทย์กำหนดมาทำโดย เริ่มเขียนตั้งแต่เซตว่าง แล้วตามด้วยเซตที่มีสมาชิก 1 ตัว, 2 ตัว ไปเรื่อยๆ จนมีสมาชิกเท่ากับเซตที่โจทย์กำหนดมา (ตัวมันเอง) โดยสมาชิกที่นำมาใช้เขียนต้องเป็นสมาชิกของเซตที่โจทย์กำหนดมาด้วย

ตัวอย่าง  จงเขียนสับเซตทั้งหมดของเซตต่อไปนี้

1. A = Ø สับเซตทั้งหมดของ A มี 1 สับเซต คือ Ø

2. B = {1} สับเซตทั้งหมดของ B มี 2 สับเซต คือ 1) Ø   2) {1}

3. C = {1,3} สับเซตทั้งหมดของ C มี 4สับเซต คือ  1) Ø   2) {1}  3) {3}   4) {1,3}

4. D = {1,3,5} สับเซตทั้งหมดของ D มี 4 สับเซต คือ1) Ø   2) {1}   3) {3}   4) {5}   5) {1,3}   6)  

   {1,5}   7) {3,5}   8) { 1,3,5}

จากตาราง พิจารณาความสัมพันธ์ของสมาชิกของเซตกับจำนวนสับเซตทั้งหมดจะได้ว่า

จำนวนสับเซตทั้งหมดของเซต A = 2^n(A)

จำนวนสับเซตแท้ทั้งหมดของ A

นิยาม : สับเซตแท้ (proper set) ของ A คือ สับเซตทั้งหมดของเซต A ยกเว้น ตัวมันเอง (ยกเว้น A)

1.มีเซตอะไรไหมที่ไม่มีสับเซตแท้
ตอบ มี เซตดังกล่าวคือเซตว่าง เพราะว่าสับเซตของ Ø ก็คือ Ø เพียงตัวเดียว ดังนั้น เซตว่างจึงไม่มีสับเซต

         แท้

2. จำนวนสับเซตแท้ของเซต A = 2^n(A)  -1   สับเซต

โจทย์ประยุกต์ เรื่อง สับเซต

ข้อ1. ถ้า A={a, b,c,d,e,f} และ B={a,b} แล้วจำนวนเซต X ซึ่ง   B⊂X⊂A เท่ากับข้อใดต่อไปนี้

1.4                                2.15                              3.16                              4.32

เฉลย.

B⊂Xแปลว่า a, b ต้องอยู่ใน X ซึ่ง X⊂Aแปลว่า c, d, e, f อยู่ใน X กี่ตัวก็ได้

∴จำนวนแบบที่เป็นไปได้ของ X ก็คือจำนวนสับเซตทุกแบบของ {c, d, e, f}

นั่นคือ 2^4=16 แบบ

ข้อ2. ถ้า A={5, 6, 7, …,20} และ B={1, 2, 3,…,15} แล้ว จำนวนสมาชิกในเซต {X | X เป็นสับเซตของ A และ X ไม่เป็นสับเซตของ B}

1. (7×2)^10                                                      2. (31×2)^11

3. (31×2)^10                                                    4. (63×2)^11

เฉลย.

คิดโดยวิธีลบออก คือ จำนวนสับเซตของ A ทุกแบบ ลบออกด้วยแบบที่เป็นสับเซตของ  B ด้วย

จะได้เท่ากับ 2^16-2^11=31×2^11

ข้อ3. กำหนดให้ S={1, 2, 3, 4, 5} , A={1} , B={5} และ A⊂X⊂S , B⊂Y⊂S จงหาว่า X∪Y มีทั้งหมดกี่เซตที่แตกต่างกัน

1.8                                2.16                              3.32                              4.64

เฉลย.

แบบต่างๆของ X คือ

{1, สับเซตทุกแบบของ 2,3, 4,5}

มีอยู่ 2^4=16 แบบ

แบบต่างๆของ Y คือ

{5, สับเซตทุกแบบของ 1, 2, 3, 4}

มีอยู่ 2^4=16 แบบ

แต่แบบต่างๆของ X∪Y จะต้องมีทั้ง 1 และ 5 อยู่ในนั้น คือ {1, 5, สับเซตทุกเเบบของ 2, 3, 4}

ดังนั้นจึงมีอยู่ 2^13= 8 แบบ

  พาวเวอร์เซต

หมายถึง เซตของสับเซต จะเขียนแทนเพาเวอร์เซตของเซต A ด้วย P(A)

วิธีหาเพาเวอร์เซต จะต้องหาสับเซตทั้งหมดให้ได้ก่อน จากนั้นจึงใส่เซตครอบลงไป

ตัวอย่าง   จงหาสับเซตทั้งหมดของ A = {2, 4, 6, 8}

ขั้นแรก : หาสับเซตก่อน ได้แก่

  Ø , {2} , {4} , {6} , {8} , {2, 4} , {2, 6} , {2, 8} , {4, 6} , {4, 8} , {6, 8} , {2, 4, 6} , {2, 6, 8} , {2, 4, 8} , {4, 6, 8} , {2, 4, 6, 8}

ดังนั้น P(A) = {Ø, {2},{4},{6},{8},{2, 4},{2, 6},{2, 8},{4, 6},{4, 8},{6, 8}, {2, 4, 6}, {2, 6, 8},{2, 4, 8},{4, 6, 8},{2, 4, 6, 8}

กำหนดให้ A เป็นเซตจำกัด ถ้าเซต A มีจำนวนสมาชิก  ตัวแล้วจำนวนสมาชิกของเพาเวอร์เซต A จะเท่ากับ 2ⁿตัว

ตัวอย่าง

1. ถ้า P(P(A)) มีสมาชิก 256 ตัว แล้วเซต A จะมีสมาชิกกี่ตัว

วิธีทำ

P(P(A)) = 256 = 2^8

P(A) = 8= 2^3

n(A) = 3

2. ถ้า n(P(A)) – n(P(B)) = 63 และn(P(A∩B)) + n(P(A∪B)) = n(P(C∩B)) + n(P(C∪B)) แล้ว จงหาค่าของ n(A) + n(B) + n(C)

วิธีทำ  

2^(n(A)) – 2^(n(B)) = 2^6 – 2^0

∴n(A) = 6 , n(B) = 0จะได้ว่า B =∅

แทนค่าได้

n(P(A∩∅)) + n(P(A∪∅)) = n(P(C∩∅)) + n(P(C∪∅))

n(P(∅)) + n(P(A)) = n(P(∅)) + n(P(C))

2^n(A)  = 2^n(C)

∴n(A) = n(C) = 6

∴n(A) + n(B) + n(C) = 6+0+6 = 12

3. กำหนดให้ A และ B เป็นเซตจำกัด โดยที่จำนวนสมาชิกของ P(A) เป็นสองเท่าของจำนวนสมาชิกของ P(B) จำนวนสมาชิกของ P(A∩B) = 8 และจำนวนสมาชิกของ P(A∪B) = 256 จงหาจำนวนสมาชิก P(A-B)

วิธีทำ

n(P(A)) = 2n(P(B))

2^(n(A))=2^1∙2^(n(B))= 2^(1+n(B))

n(A) = 1+n(B)

n(P(A∩B)) = 8 =2^(n(A∩B))

2^(n(A∩B))= 3

n(P(A∪B)) = 256 = 2^(n(A∩B))

2^(n(A∪B))= 8

∴n(P(A-B)) = 2^(n(A-B)) = 2^3 = 8

สรุป

ซับเซตและเพาเวอร์เซต ( subset & power set)