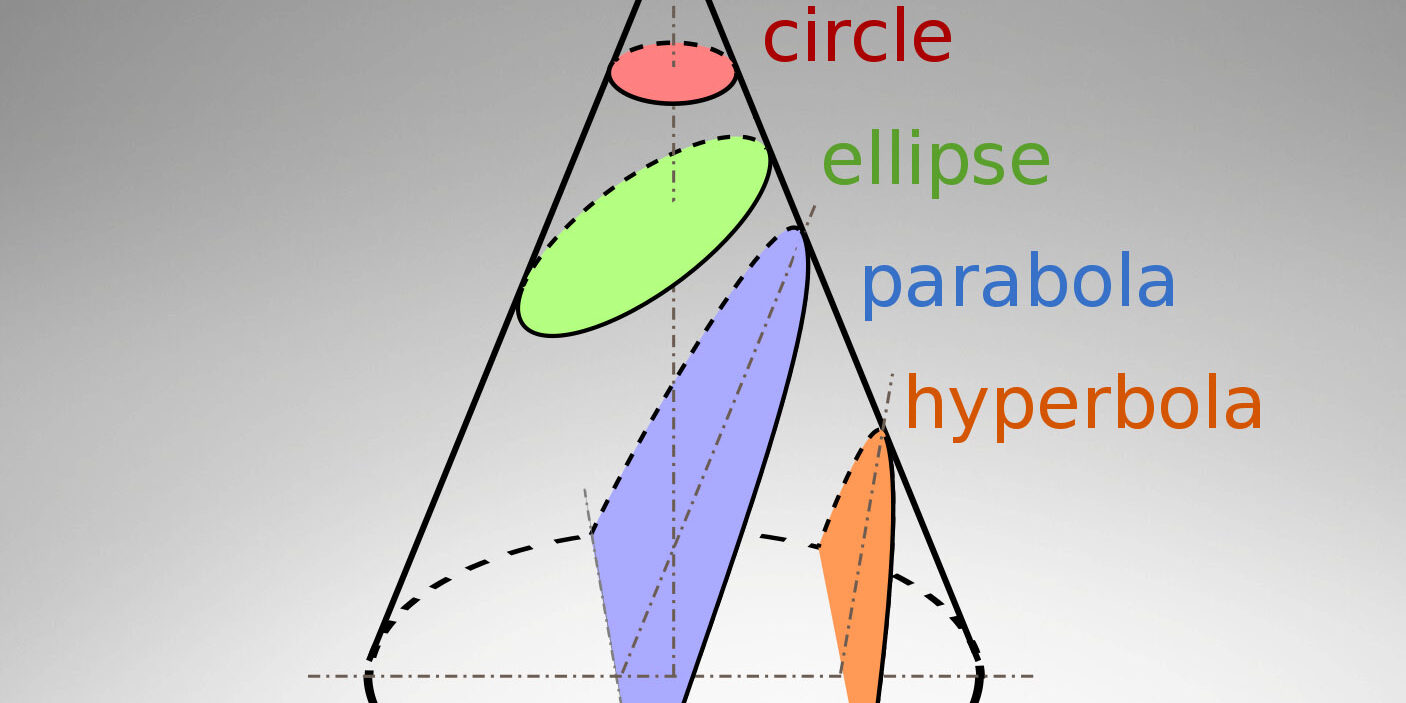
ภาคตัดกรวย

ภาคตัดกรวย เป็นศัพท์บัญญัติ จากคำว่า “conic section” ซึ่งคำว่า conic เป็นคำคุณศัพท์ที่มาจากคำว่า “cone” ที่แปลว่ากรวย

ภาคตัดกรวย (conic section หรือ conic) ในทางคณิตศาสตร์ หมายถึง เส้นโค้งที่ได้จากการตัดพื้นผิวกรวยกลม ด้วยระนาบแบน ภาคตัดกรวยนี้ถูกตั้งเป็นหัวข้อศึกษาตั้งแต่สมัย 200 ปีก่อนคริสต์ศักราชโดย อพอลโลเนียส แห่ง เพอร์กา ผู้ซึ่งศึกษาภาคตัดกรวยและค้นพบสมบัติหลายประการของภาคตัดกรวย ต่อมากรณีการศึกษาภาคตัดกรวยถูกนำไปใช้ประโยชน์หลายแบบ ได้แก่ ในปี พ.ศ. 2133 (ค.ศ. 1590) กาลิเลโอ กาลิเลอี พบว่าขีปนาวุธที่ยิงขึ้นไปในมุมที่กำหนดมีวิถีการเคลื่อนที่โค้งแบบพาราโบ ลา, ใน พ.ศ. 2152 (ค.ศ. 1609) โยฮันส์ เคปเลอร์ พบว่าวงโคจรของดาวเคราะห์รอบนอกเป็นรูปวงรี เป็นต้น

ชนิดของภาคตัดกรวย

วงกลม และ วงรี คือ เส้นโค้งซึ่งได้จากการตัดกรวย ด้วยระนาบ ให้ได้เส้นโค้งปิด (เป็นวง) วงกลมนั้นถือเป็นกรณีพิเศษของวงรี โดยแนวของระนาบในการตัดนั้น ตั้งฉากกับแกนกลางของกรวย หากระนาบตัดกรวยในแนวขนานกับเส้นขอบของกรวย หรือเรียก เส้นกำเนิดกรวย (generator line) จะได้เส้นโค้งเรียกว่า พาราโบลา หากระนาบไม่อยู่ในแนวขนานเส้นขอบ และตัดกรวยได้เส้นโค้งเปิดไม่เป็นวง จะเรียกเส้นโค้งนี้ว่า ไฮเพอร์โบลา จะเห็นได้ว่าในกรณีนี้ระนาบจะตัดกรวยทั้งครึ่งบน และครึ่งล่าง ได้เป็นเส้นโค้งที่ขาดจากกันสองเส้น

ในกรณีที่เรียกว่าในภาษาอังกฤษว่า ดีเจนเนอเรต ระนาบจะตัดผ่านจุดยอดของกรวย และได้ผลของการตัดเป็น จุด เส้นตรง หรือ เส้นตรงสองเส้นตัดกัน กรณีเหล่านี้ไม่ได้ถูกรวมไว้ในภาคตัดกรวย

เส้นโค้งที่เกิดจาการตัดกรวย ประกอบด้วย

วงกลม (Circle)
วงรี (Ellipse)
พาราโบลา (Parabola)
ไฮเพอร์โบลา (Hyperbola)

ภาคตัดกรวยจากทางเดินของจุด

แต่ละประเภทของภาคตัดกรวยนั้น สามารถนิยามโดยการใช้เส้นทางเดินของจุด โดยทุก ๆ จุด P บนเส้นทางเดิน จะต้องเป็นไปตามคุณสมบัติเฉพาะดังนี้

วงกลม : ระยะ (P, C) = r โดยที่ C คือจุดตายตัวเรียกว่า จุดศูนย์กลาง และ r คือค่าคงที่ เรียกว่า รัศมี
พาราโบลา : ระยะ (P, F) = ระยะ (P, L) โดยที่ F คือจุดตายตัว เรียกว่า จุดโฟกัส และ L คือ เส้นตรง กำหนดตายตัว และไม่ผ่านจุดโฟกัส เรียกว่า ไดเรกทริกซ์
วงรี : ระยะ (P, A) + ระยะ (P, B) = d โดยที่ A, B เป็นจุดตายตัวสองจุดที่แตกต่างกัน เรียกว่า จุดโฟกัส และ d เป็นค่าคงที่ ที่มีค่ามากกว่า ระยะ(A,B) เรียกว่า เส้นผ่านศูนย์กลางหลัก
ไฮเพอร์โบลา : ระยะ (P, A) – ระยะ (P, B) = d โดยที่ A, B เป็นจุดตายตัวสองจุดที่แตกต่างกัน เรียกว่า จุดโฟกัส และ d เป็นค่าคงที่ ที่มีค่าน้อยกว่า ระยะ (A,B)

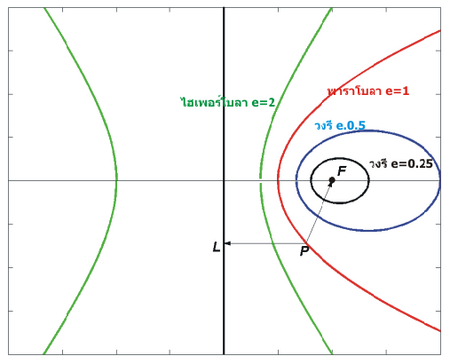
ความเยื้อง (ECCENTRICITY)

ค่าความเยื้อง หรือ ค่าความเบี่ยงเบนจากศูนย์กลาง (eccentricity) ของภาคตัดกรวย เป็นค่าบ่งชี้ถึงความเบี้ยว หรือ เบี่ยงเบนไปจากความกลม โดยเมื่อความเยื้องมีค่าลดลง รูปร่างของภาคตัดกรวยที่ได้จะมีรูปร่างเข้าใกล้ทรงกลมมากขึ้น

ถ้าเส้นตรง L คือไดเรกทริกซ์ และ F คือ จุดโฟกัส ค่าความเยื้อง e หาได้จาก

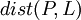$\frac{dist(P,F)}{dist(P,L)} = e \qquad e \in\mathbb{R}^*_+$