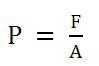สมบัติเชิงกลของสาร เรื่อง มอดูลัสของสภาพยืดหยุ่น(Young’s modulus)
สมบัติเชิงกลของสาร(ของแข็ง)
สมบัติเชิงกลของสาร (ของแข็ง)
ความยืดหยุ่น เป็นสมบัีติของวัตถุที่สามารถกลับคืนสู่สภาพเดิมหลักถูกแรงกระทำ เช่น ยางยืด
สภาพยืดหยุ่น (elasticity) คือ สมบัติของวัตถุที่มีการเปลี่ยนแปลงรูปร่างเมื่อมีแรงกระทำและสามารถคืนตัวกลับสู่สภาพเดิมเมื่อหยุดออกแรงกระทำ
สภาพพลาสติก (plasticity) คือ สมบัติของวัตถุที่มีการเปลี่ยนรูปร่างไปอย่างถาวร โดยผิววัตถุไม่ฉีกขาดหรือแตกหัก!
ขอบเขตของการยืดหยุ่น
โดยทั่วไปวัตถุที่มีความยืดหยุ่นสมบูรณ์ (กลับสู่สภาพเดิมได้จริง) จะเป็นวัตถุที่มีความยืดหยุ่นสมบูรณ์ภายในขอบเขตจำกัดเท่านั้น เรียกว่า ขอบเขตของการยืดหยุ่น
 รูปที่ 1
รูปที่ 1
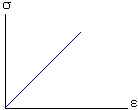
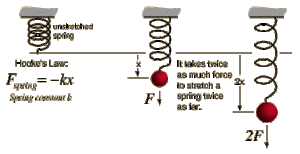
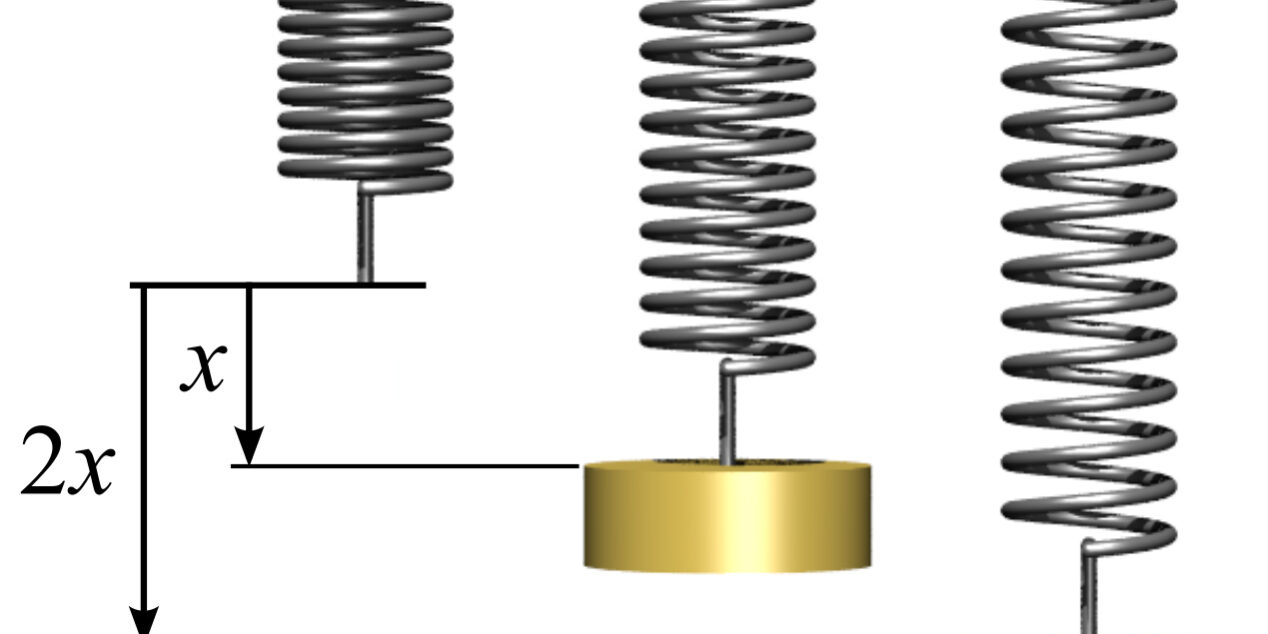
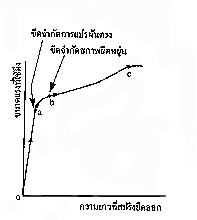
สมมติออกแรงดึงสปริงให้ยืดออก ขนาดของแรงดึงสปริงกับระยะที่ยืดออกเป็นไปตามกฏของฮุก และได้กราฟดังรูป
– จุด a คือ ขีดจำกัดการแปรผันตรง (Proportional limit) ซึ่งเป็นตำแหน่งสุดท้ายที่ความยาวสปริงยืดออก แปรผันตรงกับขนาดของแรงดึง
– จุด b คือ ขีดจำกัดสภาพยืดหยุ่น (Elastic limit) ซึ่งเป็นตำแหน่งสุดท้ายที่สปริงยืดออกแล้วกลับสู่สภาพเดิม แต่แรงดึงไม่แปรผันตรงกับระยะยืด
– จุด C คือ จุดแตกหัก (Breaking point) หมายถึงตั้งแต่จุด b เป็นต้นไป ถ้าดึงต่อไปก็ถึงจุด c ซึ่งเป็นจุดที่เส้นวัสดุขาด
ความเค้น (Stress)
แรงเค้น คือ แรงภายในของวัตถุที่ต้านแรงกระทำถ้าแรงเค้นน้อยกว่าแรงที่กระทำจะทำให้รูปร่างเปลี่ยนไป วัตถุส่วนมากจะมีรูปร่างผิดไปเล็กน้อยเมื่อมีแรงกระทำ โดยแรงที่มากระทำนั้นอาจกระทำในทิศต่าง ๆ และวัตถุเหล่านั้นส่วนใหญ่จะประพฤติตามกฎของฮุกเมื่อแรงยังน้อยกว่าขีดจำกัดสภาพยืดหยุ่น
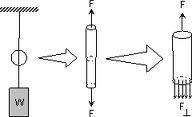 รูปที่ 2
รูปที่ 2
ความเค้น (Stress) คือ อัตราส่วนของแรงเค้นต่อพื้นที่หน้าตัด หน่วย (N/m2) ในที่นี้กล่าวเฉพาะความเค้นดึงหรือความเค้นอัด
หมายเหตุ : แรงเค้นที่ขีดจำกัดความยืดหยุ่น เป็นแรงที่มีค่าสูงสุด
ความเครียด (Strain) คือ อัตราส่วนของความยาวที่เปลี่ยนไปต่อความยาวเดิม (ไม่มีหน่วย) ในที่นี้จะกล่าวถึงเฉพาะความเครียดตามยาว
มอดูลัสความยืดหยุ่น (Elastic modulus ; E)
เมื่อออกแรงดึงและทำการวัดระยะยืด สามารถเขียนเป็นกราฟระหว่างความเค้นกับความเครียดได้ ดังรูป พิจารณาช่วงขีดจำกัดการแปรผันตรง จะได้ว่าความเค้นแปรผันตรงกับความเครียด หรือ อัตราส่วนระหว่างความเค้นต่อความเครียดมีค่าคงที่ ซึ่งค่าคงที่นี้เรียกว่า ค่ามอดูลัสความยืดหยุ่น (E)
จะได้ สำหรับค่ามอดูลัสความยืดหยุ่นของวัตถุหนึ่ง ๆ มีค่าคงที่เสมอ และ ค่ามอดูลัสความยืดหยุ่นเป็นลักษณะเฉพาะตัวของวัตถุแต่ละชนิด เมื่อออกแรงดึงเส้นวัสดุโดยไม่ให้ขนาดของแรงดึงเกินขีดจำกัดการแปรผันตรงของวัสดุ ความเค้นตามยาวจะแปรผันตรงกับความเครียดตามยาว นั่นคืออัตราส่วนระหว่างความเค้นตามยาวและความเครียดตามยาวของวัสดุชนิดหนึ่งๆ จะมีค่าคงตัว เรียกค่าคงที่นี้ว่ามอดูลัสของยัง (Young’s modulus) แทนด้วยสัญลักษณ์ Y
F ในสมการ สำหรับสปริงหรือเส้นลวด คือ กฎของฮุก (Hook ’s Law)
หมายเหตุ : วัตถุใดที่มีค่าแรงเค้นที่ขีดจำกัดความยืดหยุ่นมากแสดงว่าทนแรงภายนอกได้มาก วัตถุใดมีค่ามอดูลัสของความยืดหยุ่นมากแสดงว่าเมื่อมีแรงภายนอกมากระทำทำให้เปลี่ยนรูปร่างได้ยาก
สมบัติเชิงกลของสาร (ของเหลว)
แรงดันและความดัน
ความหนาแน่น (density, สัญลักษณ์: ρ อักษรกรีก อ่านว่า โร ) เป็นอัตราส่วนของมวลต่อปริมาตรของสาร ในระบบ S.I. มีหน่วยเป็น กิโลกรัมต่อลูกบาศก์เมตร ตามสมการ
โดยที่
- ρ คือความหนาแน่นของวัตถุ (หน่วย กิโลกรัมต่อลูกบาศก์เมตร)
- m คือมวลรวมของวัตถุ (หน่วย กิโลกรัม)
- V คือปริมาตรรวมของวัตถุ (หน่วย ลูกบาศก์เมตร)
ความรู้เพิ่มเติม
– น้ำที่อุณหภูมิ 4 องศาเซลเซียส มีความหนาแน่น 1,000 kg/m3 หรือ 103 kg/m3 ใช้เป็นค่ามาตรฐานของความหนาแน่นน้ำ
ความหนาแน่นสัมพัทธ์ หมายถึง อัตราส่วนระหว่างความหนาแน่นของสารนั้นกับความหนาแน่นของสารอ้างอิง ในอดีตเคยเรียกว่า ความถ่วงจำเพาะ
ตัวอย่าง ถ้าต้องการหาความหนาแน่นสัมพัทธ์ของสารใด ให้นำ 103 ไปหาร เช่น ปรอทมีความหนาแน่น 13.6 x 103 kg/m3
ดังนั้น ปรอทมีความหนาแน่นสัมพัทธ์ = 13.6 x 103 / 103 = 13.6
ข้อสังเกต – ความหนาแน่นสัมพัทธ์ไม่มีหน่วย
– ความหนาแน่นสัมพัทธ์ เดิมเรียกว่า ค่าความถ่วงจำเพาะของสาร
ความดัน
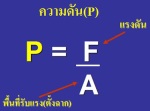
แรงดัน หรือ ความดัน คือ ขนาดของแรงดันที่กระทำตั้งฉากต่อพื้นที่หนึ่งหน่วย
ถ้าให้ F คือ แรงดัน (N) , A คือ พื้นที่ (m2) , P คือ ความดัน (N/m2)
จะได้
รูปที่ 4
ความดันเป็นปริมาณสเกลาร์ มีหน่วยนิวตันต่อตารางเมตร (N/m2) หรือพาสคัล (Pa)
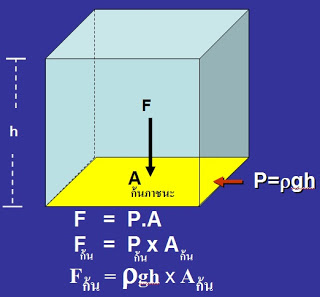
แรงดันที่กดก้นภาชนะ = น้ำหนักของของเหลวส่วนที่อยู่ในแนวตั้งฉากกับพื้นที่นั้น
นั่นคือ F = W = mg
รูปที่ 5
แรงดันน้ำที่กระทำต่อก้นภาชนะซึ่งบรรจุน้ำลึก h มีพื้นที่ก้นภาชนะ A หาแรงดันได้จากผลคูณระหว่างความดันที่ก้นภาชนะกับพื้นที่ก้นภาชนะ
หน่วยอื่น ๆ ของความดัน
1 พาสคัล (Pa) = 1 นิวตัน/ ตารางเมตร (N/m2 )
1 บาร์ (Bar) = 1.0×105 N/m2 (นิยมใช้ในทางอุตุนิยมวิทยา)
1 บรรยากาศ = 1.013×105 N/m2 = 760 มม. ของปรอท
คุณสมบัติของแรงดันและความดันในของเหลว
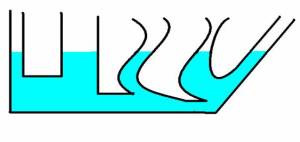
1. ของเหลวที่บรรจุอยู่ในภาชนะ จะออกแรงดันต่อผนังภาชนะที่สัมผัสกับของเหลวในทุกทิศทาง โดยจะตั้งฉากกับผนังภาชนะเสมอ
2. ทุก ๆ จุดในของเหลว จะมีแรงดันกระทำต่อจุดนั้นทุกทิศทุกทาง
รูปที่ 6
3. สำหรับของเหลวชนิดเดียวกันความดันของของเหลวจะเพิ่มขึ้นตามความลึก และที่ระดับความลึกเท่ากันความดันของเหลวจะเท่ากัน
4. ในของเหลวต่างชนิดกัน ณ ความลึกเท่ากัน ความดันของของเหลวจะขึ้นอยู่กับความหนาแน่นของของเหลวนั้น
สรุปได้ว่า
1. ของเหลวชนิดเดียวกัน ที่ความลึกเท่ากันจะมีความดันของของเหลวเท่ากัน
2. ความดันของของเหลวขึ้นอยู่กับความลึกและความหนาแน่นของของเหลว โดยมีความสัมพันธ์แบบแปรผันตรง
ปัจจัยที่มีผลต่อความดันของของเหลว
1. ความลึกของของเหลว
– ของเหลวไม่ว่าจะอยู่ในภาชนะรูปร่างใดก็ตาม ถ้าที่ระดับความลึกเดียวกัน ความดันของของเหลวจะเท่ากัน
– แต่ถ้าระดับความลึกต่างกัน ของเหลวที่อยู่ระดับลึกกว่า จะมีความดันมากกว่า
รูปที่ 9 ที่ระดับความลึกต่างกัน น้ำที่ระดับความลึกมากกว่าจะมีความดันมากกว่า
2. ความหนาแน่นของของเหลว
ของเหลวต่างชนิดกันจะมีความดันต่างกัน โดยของเหลวที่มีความหนาแน่นมาก จะมีความดันสูงกว่าของเหลวที่มีความหนาแน่นน้อย
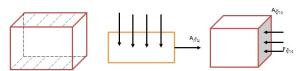
แรงที่ของเหลวกระทำต่อผนังภาชนะ
ในภาชนะที่บรรจุของเหลวจะมีแรงจากของเหลว มากระทำให้ทิศตั้งฉากกับพื้นที่ผิวภาชนะที่ของเหลวสัมผัส ขนาดของแรงที่ของเหลวกระทำ หาได้จาก ผลคูณระหว่้างความดันในของเหลวกับพื้นที่ที่ของเหลวสาัมผัส แต่เนื่องจากบางกรณีความดันไม่คงที่ อาจเนื่องมาจากความลึกไม่สม่ำเสมอ ซึ่งอาจแยกพิจารณาได้ดังต่อไปนี้
พิจารณาแรงดันของของเหลวที่กระทำต่อผนังภาชนะดังรูป
รูปที่ 10 กล่องสี่เหลี่ยมบรรจุของเหลวเต็ม
การหาแรงดันที่ของเหลวกระทำต่อก้นกล่อง
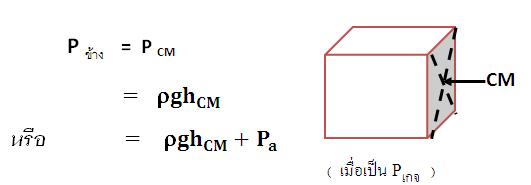
การหาแรงดันที่ของเหลวกระทำต่อผนังด้านข้าง ดังรูปที่ 10 หาได้จาก
เนื่องจากความลึกที่ผนังด้านข้างไม่คงที่ ดังนั้นความดันด้านข้างจะไม่คงที่ แต่เนื่องจากความดันแปรโดยตรงกับความลึก จึงอาจหา P ข้างได้จาก
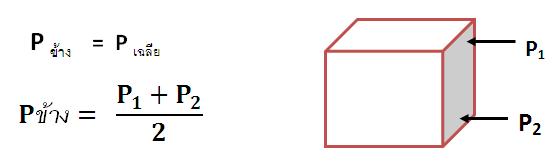 เมื่อ P1 คือ ความดันที่ปลายบนสุดของฝาด้านข้างที่สัมผัสของเหลว
เมื่อ P1 คือ ความดันที่ปลายบนสุดของฝาด้านข้างที่สัมผัสของเหลว
P2 คือ ความดันที่ปลายล่างสุดของฝาด้านข้างที่สัมผัสของเหลว
หมายเหตุ การวัดความลึกให้วัดจากผิวบนสุดของของเหลว
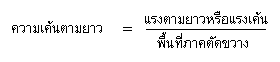
 รูปที่ 3
รูปที่ 3