สรุปสูตร เรขาคณิตวิเคราะห์ (Analytic geometry)
เรขาคณิตวิเคราะห์(Analytic Geometry) เป็นสาขาหนึ่งของวิชาคณิตศาสตร์ วิธีการทางเรขาคณิตวิเคราะห์เป็ นการศึกษาความสัมพันธ์ของหลักเกณฑ์ทางเรขาคณิตและพีชคณิตผสมผสานกัน ความคิดทางเรขาคณิตวิเคราะห์ได้ก่อตัวมานานตั้งแต่การส ารวจของชาวอียิปต์และการท าแผนที่โลกของชาวกรีก และเริ่มมีความชัดเจนมากขึ้นเมื่อปี แยร์ เดอ แฟร์มา
(Pierre de Fermat,ค.ศ.1601-1665)ได้ศึกษาผลงานทาง เรขาคณิตในสมัยก่อนๆด้วยวิธีการของเขา คือ การศึกษารูปโค้งด้วยสมการทางพีชคณิต
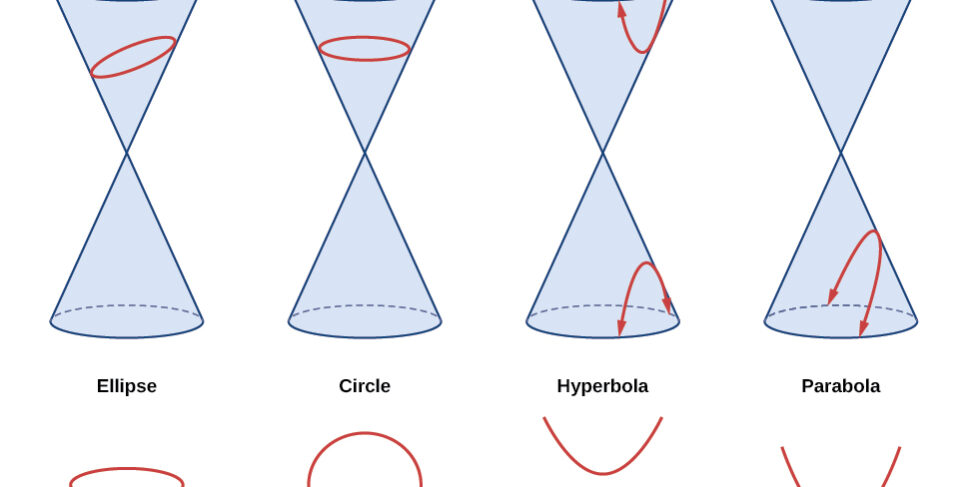
รายละเอียดเรขาคณิตวิเคราะห์ที่จะกล่าวถึงในที่นี้ประกอบไปด้วย ระยะทางระหว่างจุด 2 จุด จุดกึ่งกลางระหว่างจุด 2 จุด ความชันของเส้นตรง เส้นขนานและเส้นตั้งฉาก ระยะระหว่างจุดกับเส้นตรง และระยะทางระยะทางระหว่างเส้นตรงกับเส้นตรง
บนระบบพิกัดฉาก กำหนดจุด P 1 (x 1 ,y 1 )และจุด P 2 (x 2 ,y 2 ) อยู่บนเส้นตรง
เดียวกัน การหาระยะทางระหว่างจุด P 1และ จุด P 2สามารถหาได้ตามเงื่อนไขของพิกัดจุด
บนเส้นตรงดังนี้
กำหนด d แทน ระยะทางระหว่างจุด P 1 และ จุด P 2

จากส่วนของเส้นตรง P1 P 2 ดังรูป 9.4 กำหนดให้จุด R(x,y) เป็นจุดกึ่งกลาง
ระหว่างจุด P 1 และจุด P 2 สามารถหาพิกัดของจุดกึ่งกลางได้ดังนี้
จากรูป ลากส่วนของเส้นตรงจากจุด P1 ขนานกับแกน x และลากส่วนของเส้นตรงจากจุด P2 ขนานกับแกน y ไปตัดกันที่จุด Q
จะได้สามเหลี่ยมมุมฉาก P1 Q P2 บนส่วนของเส้นตรง P1 P 2 ให้จุด R( x , y) เป็นจุดกึ่งกลางระหว่างจุด P 1 และจุด P 2 ลาก
ส่วนของเส้นตรงจากจุด R( x , y ) ไปตั้งฉากกับ P1Q ที่จุด S(x,y) จะได้สามเหลี่ยมมุมฉากจำนวน 2 รูป คือ P1 Q P2 และ P1SR
ซึ่งเป็นสามเหลี่ยมคล้าย จากคุณสมบัติของสามเหลี่ยมคล้ายจะได้ว่า