ฟังก์ชันเอกซ์โพเนนเชียล
ฟังก์ชันเอกซ์โพเนนเชียล(Exponential Function)
จากการศึกษาในเรื่องเลขยกกำลัง ซึ่งท้ายที่สุดเราได้สนใจเลขยกกำลังที่มีฐานเป็นจำนวนจริงบวก และเลขชี้กำลังเป็นจำนวนจริงใด ๆ
แต่ได้มีนักคณิตศาสตร์ได้สังเกตเห็นว่า ถ้าเลขยกกำลังมีฐานเป็น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ ดังนี้
ถ้ากำหนดให้ a = 1 และ x เป็นจำนวนจริงใดแล้วจะได้
ax = 1x = 1
ข้อสังเกต
- ไม่ว่า x จะเป็นจำนวนจริงใด ๆ ก็ตาม 1x ก็ยังคงเท่ากับ 1 เสมอ ดังนั้นจึงไม่น่าสนใจ เนื่องจาก เราทราบว่ามันเป็นอะไรแน่ ๆ อยู่แล้ว
- เรายังไม่ทราบนะว่า เลขยกกำลังที่มีฐานเป็นจำนวนจริงบวกยกเว้น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แสดงว่าเราจะต้องสนใจศึกษาเลขยกกำลังลักษณะนี้เป็นพิเศษ ซึ่งจะกล่าวถึงใน เรื่องฟังก์ชันเอกซ์โพเนนเชียลดังนี้
ข้อกำหนด (ฟังก์ชันเอกซ์โพเนนเชียล)
ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) Î R ´ R+ / y = ax , a > 0, a ¹ 1 }
ข้อตกลง ในหนังสือคณิตศาสตร์บางเล่มให้ข้อกำหนดของฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่อยู่ในรูป f(x) = kax เมื่อ k เป็นค่าคงตัวที่ไม่ใช่ 0 และ a เป็นจำนวนจริงบวกที่ไม่เป็น 1 แต่ในหลักสูตรมัธยมศึกษาตอนปลายนี้ จะถือว่าฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป f(x) = ax เมื่อ a เป็น จำนวนจริงบวกที่ไม่เป็น 1 เท่านั้น
ข้อสังเกต จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล
- f(x) = 1x เป็นฟังก์ชันคงตัวเนื่องจาก 1x = 1 ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล จึงไม่สนใจ ฐาน (a) ที่เป็น 1
- f(x) = 1x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1x เป็นฟังก์ชันคงตัว
- จากเงื่อนไขที่ว่า y = ax, a > 0, a ¹ 1 ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ 0 < a < 1 กับ a > 1
- ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังนี้
ชนิดที่ 1 y = ax, 0 < a < 1
ชนิดที่ 2 y = ax, a > 1
นิยามของฟังก์ชันเอกซ์โพเนนเชียล
ฟังก์ชันเอกซ์โพเนนเชียล (Exponential Function)
จากการศึกษาในเรื่องเลขยกกำลัง ซึ่งท้ายที่สุดเราได้สนใจเลขยกกำลังที่มีฐานเป็นจำนวนจริงบวก และเลขชี้กำลังเป็นจำนวนจริงใด ๆ
แต่ได้มีนักคณิตศาสตร์ได้สังเกตเห็นว่า ถ้าเลขยกกำลังมีฐานเป็น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ ดังนี้
ถ้ากำหนดให้ a = 1 และ x เป็นจำนวนจริงใดแล้วจะได้
ax = 1x = 1
ข้อสังเกต
- ไม่ว่า x จะเป็นจำนวนจริงใด ๆ ก็ตาม 1x ก็ยังคงเท่ากับ 1 เสมอ ดังนั้นจึงไม่น่าสนใจ เนื่องจาก เราทราบว่ามันเป็นอะไรแน่ ๆ อยู่แล้ว
- เรายังไม่ทราบนะว่า เลขยกกำลังที่มีฐานเป็นจำนวนจริงบวกยกเว้น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แสดงว่าเราจะต้องสนใจศึกษาเลขยกกำลังลักษณะนี้เป็นพิเศษ ซึ่งจะกล่าวถึงใน เรื่องฟังก์ชันเอกซ์โพเนนเชียลดังนี้
ข้อกำหนด (ฟังก์ชันเอกซ์โพเนนเชียล)
ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) Î R ´ R+ / y = ax , a > 0, a ¹ 1 }
ข้อตกลง ในหนังสือคณิตศาสตร์บางเล่มให้ข้อกำหนดของฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่อยู่ในรูป f(x) = kax เมื่อ k เป็นค่าคงตัวที่ไม่ใช่ 0 และ a เป็นจำนวนจริงบวกที่ไม่เป็น 1 แต่ในหลักสูตรมัธยมศึกษาตอนปลายนี้ จะถือว่าฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป f(x) = ax เมื่อ a เป็น จำนวนจริงบวกที่ไม่เป็น 1 เท่านั้น
ข้อสังเกต จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล
- f(x) = 1x เป็นฟังก์ชันคงตัวเนื่องจาก 1x = 1 ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล จึงไม่สนใจ ฐาน (a) ที่เป็น 1
- f(x) = 1x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1x เป็นฟังก์ชันคงตัว
- จากเงื่อนไขที่ว่า y = ax, a > 0, a ¹ 1 ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ 0 < a < 1 กับ a > 1
- ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังนี้
ชนิดที่ 1 y = ax, 0 < a < 1
ชนิดที่ 2 y = ax, a > 1
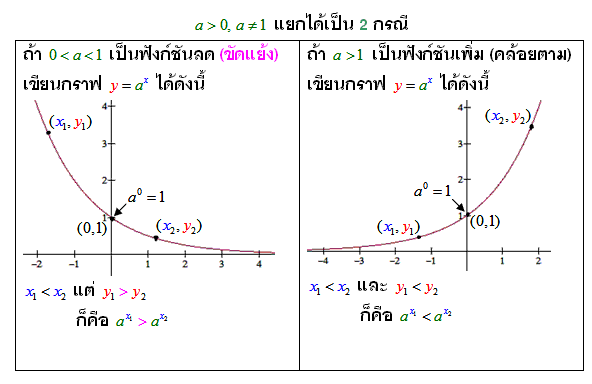
กราฟของฟังก์ชัน y = ax, 0 < a < 1
สมบัติของฟังก์ชันเอกซ์โพเนนเชียล
สมบัติที่สำคัญของฟังก์ชันเอกซ์โพเนนเชียล
- เมื่อ a > 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันเพิ่ม และเมื่อ 0 < a < 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันลด
- ไม่มีค่าสูงสุดและค่าต่ำสุดของฟังก์ชัน
- กราฟของฟังก์ชันจะผ่านจุด (0, 1) และจะอยู่เหนือแกน X เสมอ
- โดเมนของฟังก์ชันเป็นจำนวนจริง (R) และเรนจ์ของฟังก์ชันเป็นจำนวนจริงบวก
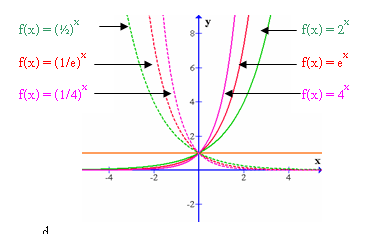
- เมื่อ a มีค่ามาก ๆ กราฟของฟังก์ชันจะเรียวยาว
- แกน y จะเป็นแกนสมมาตรของกราฟของฟังก์ชัน y = ax และ y = (1/2)x
- กราฟของฟังก์ชันเอกซ์โพเนนเชียลบนระนาบ X’Y’ มีจุดกำเนิดที่ (h,k) เทียบกับระนาบ XY มีจุดกำเนิดที่ (0, 0) จะมีสมการเป็น y- k = ax-h
- ax = ay ก็ต่อเมื่อ x = y
- ถ้า ax > ay แล้ว x > y เมื่อ a > 1
- ถ้า ax > ay แล้ว x < y เมื่อ 0 < a < 1
ฟังก์ชันชี้กำลังที่สำคัญถูกนำมาใช้ในศาสตร์อย่างหลากหลาย ได้แก่ฟังก์ชัน
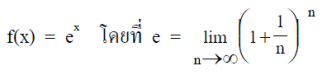
โดยค่า e 2.7182818284504523536 จำนวนจริง e นี้ ถูกค้นพบโดยนักคณิตศาสตร์และนักฟิสิกส์ชาวสวิสเซอร์แลนด์ ชื่อ เลออนฮาร์ด ออยเลอร์ (Leonhard Euler) ค.ศ. 1707-1783
สมการเอกซ์โพเนนเชียล
สมการเอกซ์โพเนนเชียล
สมการที่มีตัวแปรเป็นเลขชี้กำลัง เรียกว่าสมการเอกซ์โพเนนเชียล (exponential equation) ในการหาคำตอบของสมการเอกซ์โพเนนเชียล อาจทำได้โดยอาศัยลอการิทึม ดังตัวอย่างต่อไปนี้
การแก้สมการเอกซ์โพเนนเชียล
หลักการ
กำหนดให้ a > 0 , a ¹ 1 และ b > 0 , b ¹ 1
- aD = ar ก็ต่อเมื่อ D = r (พยายามทำฐานให้เหมือนกัน)
- ถ้า aD = ar และ a ¹ b แล้ว D = r = 0 เท่านั้น
- บางครั้งอาจจะต้องสมมุติเพื่อเปลี่ยนตัวแปรให้อยู่ในรูป Quadratic และอาจต้องใช้วิธีแยกแฟกเตอร์โพเนนเชียลง่ายขึ้น
สิ่งที่ควรเน้น คำตอบที่ได้จากการแก้สมการ ไม่ต้องนำมาตรวจสอบคำตอบ
ยกเว้นในกรณีมีการยกกำลังจำนวนคู่ จะต้องตรวจสอบคำตอบด้วย
ตัวอย่างที่ 1 จงหาค่า x ที่ทำให้สมการ 3x+2 = 243 เป็นจริง
วิธีทำ 3x+2 = 243
3x+2 = 35
x+2 = 5
ดังนั้น x = 3
ตัวอย่างที่ 2 จงแก้สมการ 10x – 5x-1 × 2x-2 = 950
วิธีทำ 10x – 5x-1 × 2x-2 = 950
10x – = 950
10x – = 950
10x(1-) = 950
10x() = 950
10x = 1000
10x = 103
x = 3
ดังนั้น เซตคำตอบของสมการคือ { 3 }
อสมการเอกซ์โพเนนเชียล
อสมการเอกซ์โพเนนเชียล
เทคนิคชุดที่ 1
การแก้อสมการเอกซ์โพเนนเชียลที่ทำฐานให้เหมือนกันได้
หลักการ
- ถ้า 0 < a < 1 (ฟังก์ชันลด) แล้ว
- ax1 > ax2 ก็ต่อเมื่อ x1 < x2
- ax1 < ax2 ก็ต่อเมื่อ x1 > x2
ข้อสังเกต
- ถ้า a > 1(ฟังก์ชันเพิ่ม) แล้ว
- ax1 > ax2 ก็ต่อเมื่อ x1 > x2
- ax1 < ax2 ก็ต่อเมื่อ x1 < x2
ข้อสังเกต ปลดฐาน หรือเติมฐาน คงเดิมเครื่องหมายอสมการ






