ความเป็นมาของตรีโกณมิติ
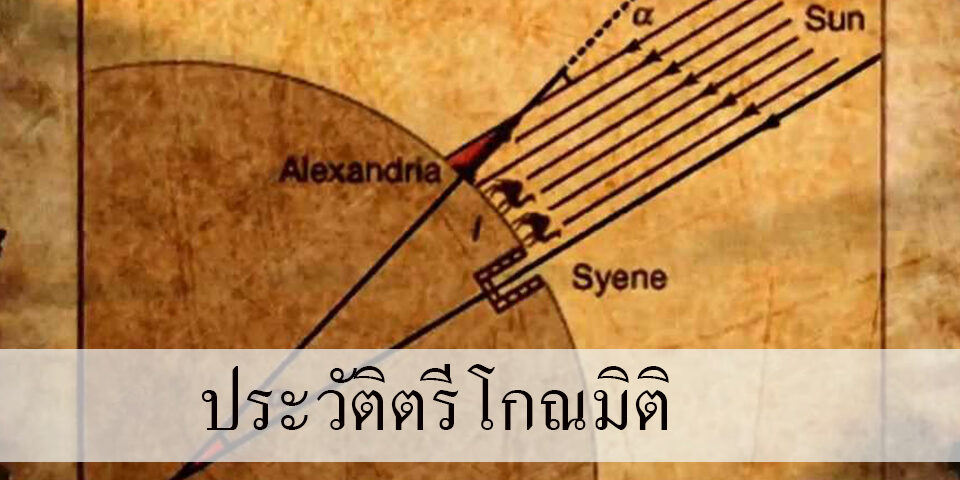
เมื่อ 640-546 ปี ก่อนครีสต์ศักราช ทาเรสได้คำนวณหาความสูง ของพีรามิด ในประเทศอียิปต์โดยอาศัยเงา วิธีหนึ่งที่ทาเรสใช้คือคำนวณความสูงของพีรามิดจากความยาวของเงาของพีรามิด ในขณะที่เงาของเขามีความยาวเท่ากับความสูงของเขาเอง  อีกวิธีหนึ่งที่ทาเรสใช้คำนวณความสูงของพีรามิดคือ  การเปรียบเทียบความยาวของเงาของพีรามิดกับความยาวของเงาของไม้(ไม้ที่ทราบความยาว ถ้าสมัยนี้ก็คือไม้เมตรนั่นเอง)  โดยอาศัยรูปสามเหลี่ยมคล้าย   ซึ่งก็คือ  อัตราส่วนตรีโกณมิติที่เรียกว่า แทนเจนต์(tangent)  นั่นเอง  ก่อนจะไปศึกษาควรรู้จัก สมบัติของสามเหลี่ยมมุมฉากก่อน
สมบัติของสามเหลี่ยมมุมฉาก
รูปสามเหลี่ยมมุมฉาก (right, right-angled, rectangled) มีมุมภายในมุมหนึ่งมีขนาด 90° (มุมฉาก) ด้านที่อยู่ตรงข้ามกับมุมฉากเรียกว่า ด้านตรงข้ามมุมฉาก ซึ่งเป็นด้านที่ยาวที่สุดในรูปสามเหลี่ยมอีกสองด้านเรียกว่า  ด้านประกอบมุมฉาก ความยาวด้านของรูปสามเหลี่ยมมุมฉากสัมพันธ์กันตามทฤษฎีบทพีทาโกรัส นั่นคือกำลังสองของความยาวของด้านตรงข้ามมุมฉาก c จะเท่ากับผลบวกของกำลังสองของด้านประกอบมุมฉาก a, b เขียนอย่างย่อเป็น

มนุษย์กับสิ่งแวดล้อมมีความสัมพันธ์ต่อกัน มนุษย์สังเกตปรากฎการณ์ทางธรรมชาติต่าง ๆ โดยเฉพาะในเรื่องดาราศาสตร์ เพราะเป็นเรื่องที่พบเห็นทุกวัน เริ่มตั้งแต่การขึ้น ตก ของดวงอาทิตย์ ดวงจันทร์ และดวงดาวต่าง ๆ หากเราสังเกตการเปลี่ยนแปลงของตำแหน่งดวงดาวต่าง ๆ เมื่อเทียบกับเวลาต่าง ๆ ในรอบปี เราจะพบกับสิ่งที่ชวนคิดหลาย ๆ อย่าง เช่น ดวงอาทิตย์ขึ้นตำแหน่งเดียวกันตลอดทั้งปีหรือไม่ ทำไมแต่ละวันดวงอาทิตย์จึงขึ้นจากขอบฟ้าไม่ตรงเวลาเดียวกัน ความคิดในเรื่องทรงกลมท้องฟ้าที่มองเห็นทำให้เกิดจินตนาการ และหาหนทางเรียนรู้ โดยใช้วิชาการทางคณิตศาสตร์ ต้นตำรับความคิดทางตรีโกณมิติ จึงมาจากสามเหลี่ยมทรงกลมท้องฟ้า ความสำคัญในเรื่องการคำนวณเกี่ยวข้องกับทรงกลมมีมาก่อนการนำมาใช้ในเรื่องสามเหลี่ยมแนวราบ โดยสามารถนำเอาหลักการทางตรีโกณมิติมาใช้แก้ปัญหาภายหลัง

ความผูกพันในเรื่องทรงกลมในสมัยเริ่มต้นมีหลักฐานว่า ฮิปพาร์ชุส (Hipparchus) ได้เขียนตารางตรีโกณมิติไว้ตั้งแต่เมื่อ 140 ปี ก่อนคริสตกาล ตารางการคำนวณในสมัยนั้นเน้นการหาความยาวส่วนโค้งของวงกลม เมื่อวงกลมมีรัศมีหนึ่งหน่วย จากตารางที่แสดงให้เห็นว่า เมื่อค่า มีค่าต่าง ๆ กัน ค่าของส่วนโค้งจะแปรเปลี่ยนไป ตารางที่ฮิปพาร์ชุสเขียนไว้ได้สูญหายไปหมด ซึ่งจะเห็นว่า ตัวเลขที่เป็นธรรมชาติมีหลายตัว และมีการค้นคว้ากันมาเรื่อย ๆ ต่อมามีการแบ่งมุมรอบจุดศูนย์กลางของวงกลมเป็น 360 องศา และจากแนวความคิดนี้ พโทเลมีนำเอามุม 360 องศา และแบ่งเส้นผ่านศูนย์กลางเป็นส่วน 120 ส่วน และคำนวณอัตราส่วนของเส้นรอบรูปต่อเส้นผ่านศูนย์กลางได้ค่าเป็น ในยุคแรก ๆ กำหนดให้มีค่าโดยประมาณเท่ากับ 3

ความคิดเชิงทฤษฎีเรขาคณิตจงเกิดขึ้นอย่างต่อเนื่อง มีการสร้างทฤษฎีทางเรขาคณิตที่ว่าด้วย เส้น มุม ส่วนโค้งของวงกลม ทำให้การคำนวณเจริญก้าวหน้ามาเป็นลำดับ

ตัวเลขธรรมชาติที่เกี่ยวกับ sin x cos x และ tan x จึงเป็นที่รู้จักกันแพร่หลายและนำมาใช้ประโยชน์ พโทเลมียังทราบความสัมพันธ์ของ
sin2x + cos2x = 1 และสามารถพิสูจน์

จากความคิดในเรื่องส่วนโค้งของวงกลมและรัศมี ทำให้การคิดคำนวณหาค่าของสัดส่วนทางตรีโกณมิติ ในเวลาต่อมาในรูปของด้านของสามเหลี่ยมมุมฉาก ซึ่งก็คือสัดส่วนของด้านต่างๆ และพิจารณาเฉพาะสามเหลี่ยมมุกฉากเท่านั้น ทำให้วิชาตรีโกณมิติสมัยใหม่จึงเน้นเฉพาะรูปสามเหลี่ยม ซึ่งมีสัดส่วนที่สำคัญเช่นเดียวกับหลักการทางด้านวงกลม และส่วนโค้ง คือ

ค่าของ sinคือ อัตราส่วนระหว่างด้านตรงข้ามมุม กับด้านตรงข้ามมุมฉาก
ค่าของ cosinคือ อัตราส่วนระหว่างด้านประชิดมุม กับด้านตรงข้ามมุมฉาก
ค่าของ tangentคือ อัตราส่วนระหว่างด้านตรงข้ามมุม กับด้านประชิดมุม

ตรีโกณมิติวนนี้

ปัจจุบัน มีการนำตรีโกณมิติไปใช้ในงานสาขาต่างๆ เช่น เป็นเทคนิคในการสร้างรูปสามเหลี่ยม ซึ่งใช้ในวิชาดาราศาสตร์เพื่อวัดระยะทางของดาวที่อยู่ใกล้ ในภูมิศาสตร์ใช้วัดระยะทางระหว่างหลักเขตที่ดิน และใช้ในดาวเทียมนำทาง งานที่มีการใช้ประโยชน์จากตรีโกณมิติ ได้แก่ ดาราศาสตร์ (และการนำทางในมหาสมุทร บนเครื่องบิน และในอวกาศ) ,ทฤษฎีดนตรี, สวนศาสตร์, ทัศนศาสตร์, การวิเคราะห์ตลาดการเงิน, อิเล็กทรอนิกส์, ทฤษฎีความน่าจะเป็น, สถิติศาสตร์, ชีววิทยา, การสร้างภาพทางการแพทย์ (การกราดภาพตัดขวางใช้คอมพิวเตอร์ช่วย (CAT scans) และ คลื่นเสียงความถี่สูง) , เภสัชศาสตร์, เคมี, ทฤษฎีจำนวน (รวมถึง วิทยาการเข้ารหัสลับ) , วิทยาแผ่นดินไหว, อุตุนิยมวิทยา, สมุทรศาสตร์, วิทยาศาสตร์กายภาพสาขาต่างๆ, การสำรวจพื้นดิน และภูมิมาตรศาสตร์, สถาปัตยกรรม, สัทศาสตร์, เศรษฐศาสตร์, วิศวกรรมไฟฟ้า, วิศวกรรมเครื่องกล, วิศวกรรมโยธา, เรขภาพคอมพิวเตอร์, การทำแผนที่, ผลิกศาสตร์

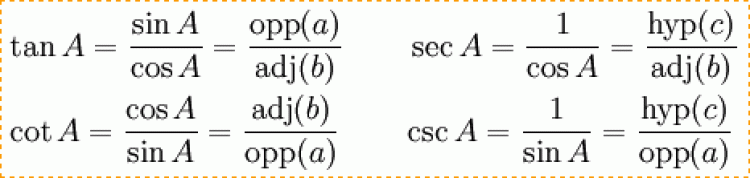
วิธีจำ ไซน์ โคไซน์ แทนเจนต์ อย่างง่ายๆคือจำว่า ข้ามฉาก ชิดฉาก ข้ามชิด (ไซน์-ด้านตรงข้าม-ด้านตรงข้ามมุมฉาก โคไซน์-ด้านประชิด-ด้านตรงข้ามมุมฉาก แทนเจนต์-ด้านตรงข้าม-ด้านประชิด)

ที่ผ่านมา ฟังก์ชันตรีโกณมิติถูกนิยามขึ้นสำหรับมุมระหว่าง 0 ถึง 90 องศา (0 ถึง /2 เรเดียน) เท่านั้น หากใช้วงกลมหนึ่งหน่วย จะขยายได้เป็นจำนวนบวกและจำนวนลบทั้งหมด

ครั้งหนึ่ง ฟังก์ชันไซน์และโคไซน์ถูกจัดลงในตาราง (หรือคำนวณด้วยเครื่องคิดเลข) ทำให้ตอบคำถามทั้งหมดเกี่ยวกับรูปสามเหลี่ยมใดๆ ได้อย่างแท้จริง โดยใช้กฎไซน์ และ กฎโคไซน์

กฎเหล่านี้สามาถใช้ในการคำนวณมุมที่เหลือและด้านของรูปสามเหลี่ยมได้ เมื่อรู้ความยาวด้านสองด้านและขนาดของมุมหนึ่งมุม หรือรู้ขนาดของมุมสองมุมและความยาวของด้านหนึ่งด้าน หรือ รู้ความยาวของด้านทั้งสามด้าน

ได้รับข้อมูลจาก : https://sites.google.com/site/suthee5678/home/prawati-trikonmiti-fil-seiyng