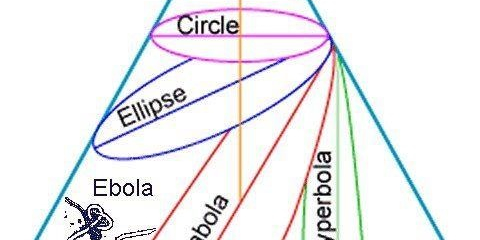
กราฟและสมการของภาคตัดกรวย
กราฟและสมการของภาคตัดกรวยแต่ละชนิด โดยอาศัยหลักการเลื่อนกราฟ ได้ดังตารางต่อไปนี้
| ภาคตัดกรวย | กราฟ | สมการรูปแบบมาตรฐานและข้อเท็จจริงที่สำคัญ |
| วงกลม | 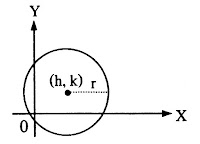 |
สมการ
จุดศูนย์กลาง (h, k) รัศมียาว r หน่วย |
| วงรี | 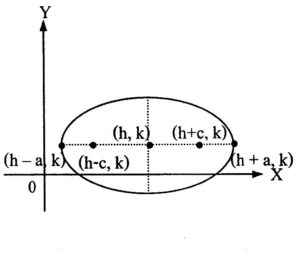 |
สมการ
แกนเอกอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c2= a2 – b2 แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย |
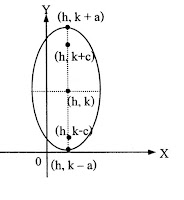 |
สมการ
แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c2= a2 – b2 แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย |
|
| พาราโบลา | สมการ
แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h, k+p) P > 0 เส้นโค้งหงายขึ้น P < 0 เส้นโค้งคว่ำลง ไดเรกตริกซ์ y = k – p |
|
| สมการ
แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h+p, k) P > 0 เส้นโค้งเปิดด้านขวา P < 0 เส้นโค้งเปิดด้านซ้าย ไดเรกตริกซ์ x = h – p |
||
| ไฮเพอร์โบลา | 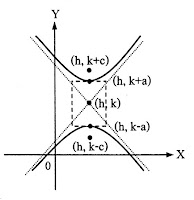 |
สมการ
แกนตามขวางอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c2= a2 + b2 แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย |
| สมการ
แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c2= a2 + b2 แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย |
สมการทั่วไปของภาคตัดกรวย
กราฟของสมการ เมื่อ A และ C ไม่เป็นศูนย์พร้อมกันเป็นภาคตัดกรวยหรือภาคตัดกรวยลดรูป ในกรณีที่ไม่ใช่ภาคตัดกรวยลดรูป กราฟของสมการเป็น
- วงกลม ถ้า A = C
- วงรี ถ้า AC > 0
- พาราโบลา ถ้า AC = 0
- ไฮเพอร์โบลา ถ้า AC < 0
สามารถค้นคว้าเนื้อหาเพิ่มเติมได้ที่
http://www.kr.ac.th/ebook/pasit/b4.htm