เซต (Set)
ความหมายของเซต
ในทางคณิตศาสตร์ คำว่า “เซต” หมายถึง กลุ่ม หมู่ เหล่า กอง ฝูง ชุด เเละเมื่อกล่าวถึงเซตของสิ่งใดๆ จะทราบได้ทันทีว่าในเซตนั้นมีอะไรบ้าง เราเรียกสิ่งที่อยู่ในเซตว่า ‘สมาชิก’
สัญลักษณ์ที่ใช้แทนเซต ชื่อเเละสมาชิกของเซต
1. สามารถใช้วงกลม, วงรี แทนเซตต่างๆ ได้
2. ชื่อเซตนิยมใช้ตัวใหญ่ทั้งหมด เช่น A, B, C, …
3. สัญลักษณ์ ∈ แทนคำว่า ” เป็นสมาชิกของ ”
∉ แทนคำว่า ” ไม่เป็นสมาชิกของ ”
ลักษณะของเซต
เซตว่าง (Empty Set) คือ เซตที่ไม่มีสมาชิก เขียนแทนด้วย ” { } ” หรือ ∅
เช่น เซตของจำนวนเต็มที่อยู่ระหว่าง 1 กับ 2
เซตของสระในคำว่า ” อรวรรณ ”
เซตจำกัด (Finite Set) คือ เซตที่สามารถบอกจำนวนสมาชิกได้
เช่น ∅ มีจำนวนสมาชิกเป็น 0
{ 1, 2, 3, … , 50 } มีจำนวนสมาชิกเป็น 50
เซตอนันต์ (Infinite Set) คือ เซตที่ไม่ใช่เซตจำกัด ไม่สามารถบอกจำนวนสมาชิกได้
เช่น เซตของจำนวนเต็มบวก {1, 2, 3, 4, … }
เซตของจุดบนระนาบ
การเขียนเซต
1. การเขียนแบบแจกแจงสมาชิก (Tabular form)
หลักการเขียน
1. เขียนสมาชิกทั้งหมดในวงเล็บปีกกา
2. สมาชิกเเต่ละตัวคั่นด้วยเครื่องจุลภาค (,)
3. สมาชิกที่ซ้ำกันให้เขียนเพียงตัวเดียว
4. ในกรณีที่มีจำนวนสมาชิกมากๆ ให้เขียนสมาชิกอย่างน้อย 3 ตัว เเล้วใช้จุด 3 จุด (Tripple dot) เเล้วจึงเขียนสมาชิกตัวสุดท้าย
2. การเขียนเซตแบบบแกเงื่อนไขของสมาชิกในเซต (Set builder form)
หลักการเขียน
1. เขียนเซตด้วยวงเล็บปีกกา
2. กำหนดตัวแปรแทนสมาชิกทั้งหมดตามด้วยเครื่องหมาย l ( l อ่านว่า โดยที ) เเล้วตามโดยเงื่อนไขของตัวแปรนั้น ดังรูปแบบ { x l เงื่อนไขของ x }
ความสัมพันธ์ของเซต
1. เซตที่เท่ากัน (Equal Sets) คือ เซตสองเซตจะเท่ากัน ก็ต่อเมื่อ เซตทั้งสองมีสมาชิกเหมือนกัน
สัญลักษณ์ เซต A เท่ากับ เซต B แทนด้วย A = B
เซต A ไม่เท่ากับ เซต B แทนด้วย A ≠ B
2. เซตที่เทียบเท่ากัน (Equivalent Sets) คือ เซตที่มีจำนวนสมาชิกเท่ากัน และสมาชิกของเซตจับคู่กันได้พอดีแบบหนึ่งต่อหนึ่ง
สัญลักษณ์ เซต A เทียบเท่ากับ เซต B แทนด้วย A ⟷ B
* หมายเหตุ 1. ถ้า A = B แล้ว A ⟷ B
2. ถ้า A ⟷ B แล้ว ไม่อาจสรุปได้ว่า A = B
สับเซต (Subset)
ถ้า สมาชิกทุกตัวของเซต A เป็นสมาชิกในเซต B เเล้ว เซต A จะเป็นสับเซตของเซต B
สัญลักษณ์ เซต A เป็นสับเซตของเซต B เขียนแทนด้วย A ⊂ B
เซต B ไม่เป็นสับเซตของเซต A เขียนแทนด้วย A ⊄ B
สมบัติของสับเซต
1. A ⊂ A ( เซตทุกเซตเป็นสับเซตของมันเอง )
2. A ⊂ U ( เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)
3. ∅ ⊂ A ( เซตว่างเป็นสับเซตของทุกๆ เซต)
4. ถ้า A ⊂ ∅ เเล้ว A = ∅
5. ถ้า A ⊂ B เเละ B ⊂ C เเล้ว A ⊂ C (สมบัติการถ่ายทอด)
6. A = B ก็ต่อเมื่อ A ⊂ B เเละ B ⊂ A
7. ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2^n ( 2 ยกกำลัง n ) สับเซต
สับเซตแท้
นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A ⊂ B เเละ A ≠ B
ตัวอย่าง กำหนดให้ A = { a, b, c } จงหาสับเซตแท้ทั้งหมดของ A
วิธีทำ สับเซตแท้ของ A ได้แก่ ∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}
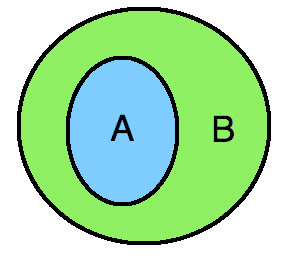
หมายเหตุ ถ้า A มีจำนวนสมาชิก n ตัว สับเซตแท้ของเซต A จะมีทั้งสิ้น 2^n-1 (2 ยกกำลัง n-1) สับเซต เราสามารถเขียนความสัมพันธ์ของสับเซตออกมาในรูปแผนภาพได้ดังนี้
A ⊂ B
เพาเวอร์เซต (Power Set)
ถ้า A เป็ตเซต เเล้ว เพาเวอร์เซตของเซต A คือ เซตที่มีสมาชิกประกอบไปด้วยสับเซตของ A ทั้งหมด
สัญลักษณ์ เพาเวอร์เซตของเซต A เขียนแทนด้วย P(A) = {สับเซตทั้งหมดของ A}
ตัวอย่าง A = {1, 2}
วิธีทำ สับเซตของ A คือ ∅, {1}, {2}, A
ดังนั้น P(A) = { ∅, {1}, {2}, A }
สมบัติของเพาเวอร์เซต
กำหนดให้ A และ B เป็นเซตใดๆ
1. ∅ ∈ P(A) เพราะ ∅ ⊂ A เสมอ
2. ∅ ⊂ P(A) เพราะเซตว่างเป็นสับเซตของทุกเซต เเล้ว P(A) ก็เป็นเซตเช่นกัน
3. A ∈ P(A) เพราะ A ⊂ A เสมอ
4. ถ้า A เป็นเซตจำกัด เเละ n(A) คือจำนวนสมชิกของ A เเล้ว P(A) จะมีสมาชิก 2^ n(A) ( 2 ยกกำลัง n(A) ) ตัว (เท่ากับจำนวนสับเซตของ A)
5. A ⊂ B ก็ต่อเมื่อ P(A) ⊂ P(B)
6. P(A) ∩ P(B) = P(A ∩ B)
7. P(A) ∪ P(B) ⊂ P(A ∪ B)
เอกภพสัมพัทธ์ (Relative Universe)
เอกภพสัมพัทธ์ คือ เซตที่ถูกกำหนดขึ้นโดยมีข้อตกลงว่า จะกล่าวถึงสิ่งที่เป็นสมาชิกของเซตนี้เท่านั้น จะไม่กล่าวถึงสิ่งอื่นใดที่ไม่เป็นสมาชิกของเซตนี้ โดยทั่วไปจะใช้สัญลักษณ์ U แทนเซตที่เป็นเอกภพสัมพัทธ์
ตัวอย่างที่ 1 กำหนดให้ U = {1, 2, 3, 4, 5, 6, 7, 8]
A = {1, 3, 5, 7}
B = {2, 4, 8}
ตัวอย่างที่ 2 กำหนดให้ U = { x ∈ N | 1 < x < 20 }
A = { x ∈ N | x = n + 3 เมื่อ n เป็นจำนวนนับคี่ }
B = { x ∈ N | x = n + 3 เมื่อ n เป็นจำนวนนับคู่ }
นั่นคือ ทั้ง A และ B เป็นสับเซตของ U






