ทฤษฎีสัมพัทธภาพพิเศษ (Special Relativity )จะเกี่ยวข้องกับระบบที่มีความเร็วคงที่คือเป็น ระบบที่ไม่มีความเร่ง การอธิบายทฤษฎีนี้อย่างง่ายที่สุดก็เปรียบเทียบให้เห็นว่า เมื่อเรารู้สึกว่าทุกสิ่งกำลังหยุดนิ่งหรือมีความเร็วที่เท่ากันเราไม่สามารถบอกได้ว่าสิ่งใดกำลังเคลื่อนที่ เช่น โลกหมุนรอบตัวเองและรอบดวงอาทิตย์ เรายัง รู้สึกว่าทุกสิ่งกำลังอยู่กับที่ แต่ที่จริงสิ่งที่เรานึกว่าหยุดอยู่กับที่กลับเคลื่อนที่
ทฤษฎีสัมพัทธภาพพิเศษ (Special Relativity) ถูกเสนอขึ้นในปี ค.ศ. 1905 โดยอัลเบิร์ต ไอน์สไตน์ ในบทความของเขา “เกี่ยวกับพลศาสตร์ไฟฟ้าของวัตถุซึ่งเคลื่อนที่ (On the Electrodynamics of Moving Bodies)” สามศตวรรษก่อนหน้านั้น หลักสัมพัทธภาพของกาลิเลโอกล่าวไว้ว่า การเคลื่อนที่ ด้วยความเร็วคงที่ทั้งหมดเป็นการสัมพัทธ์ และไม่มีสถานะของการหยุดนิ่งสัมบูรณ์และนิยามได้ คนที่อยู่บนดาดฟ้าเรือคิดว่าตนอยู่นิ่ง แต่คนที่สังเกตบนชายฝั่งกลับบอกว่า ชายบนเรือกำลังเคลื่อนที่ ทฤษฏีของไอน์สไตน์รวมหลักสัมพัทธภาพของกาลิเลโอเข้ากับสมมติฐานที่ว่า ผู้สังเกตทุกคนจะวัดอัตราเร็วของแสงได้เท่ากันเสมอ ไม่ว่าสภาวะการเคลื่อนที่เชิงเส้นด้วยความเร็วคงที่ของพวกเขาจะเป็นอย่างไร
ทฤษฏีนี้มีข้อสรุปอันน่าประหลาดใจหลายอย่างซึ่งขัดกับสามัญสำนึก แต่สามารถพิสูจน์ได้ด้วยการทดลอง ทฤษฏีสัมพัทธภาพพิเศษล้มล้างแนวคิดของสเปซสัมบูรณ์และเวลาสัมบูรณ์ของนิวตันโดยการยืนยันว่า ระยะทางและเวลาขึ้นอยู่กับผู้สังเกต และเวลากับสเปซนั้นถูกรับรู้ต่างกันไปขึ้นอยู่กับผู้สังเกต มันนำมาซึ่งหลักการสมมูลของสสารและพลังงาน ซึ่งสามารถแสดงเป็นสมการชื่อดัง E=mc2เมื่อ c คืออัตราเร็วของแสง ทฤษฎีสัมพัทธภาพพิเศษสอดคล้องกับกลศาสตร์นิวตันในสำนึกทั่วไปและในการทดลองเมื่อความเร็วของสิ่งต่างๆ น้อยมากเมื่อเทียบกับอัตราเร็วแสง
ไอน์สไตน์เขียนสมการอันโด่งดัง “เพียงชิ้นเดียว” ที่อยู่ในความครอบครองของเอกชน
ไอน์สไตน์เผยถึงสมการ E=mc² ต่อสาธารณชนเป็นครั้งแรก ในการตีพิมพ์บทความลงวารสารวิชาการเมื่อปี 1905 โดยสมการที่รู้จักกันอย่างแพร่หลายนี้ อธิบายถึงหลักความสมมูลระหว่างมวล (m) และพลังงาน (E) เมื่อวัตถุเคลื่อนที่ด้วยความเร็วแสง (c)
สมการนี้ได้ปฏิวัติวงการฟิสิกส์ โดยพิสูจน์ว่าเวลาไม่ใช่สิ่งสัมบูรณ์ และพลังงานกับมวลนั้นแท้จริงแล้วเป็นสิ่งเดียวกัน โดยพลังงานที่เกิดขึ้นจะมีค่าเท่ากับมวลคูณด้วยความเร็วแสงยกกำลังสอง
จดหมายของไอน์สไตน์ฉบับนี้ลงวันที่ 26 ตุลาคม 1946 มีความยาวหนึ่งหน้ากระดาษและเขียนด้วยภาษาเยอรมัน โดยไอน์สไตน์เขียนถึง ลุดวิก ซิลเบอร์สไตน์ นักฟิสิกส์ชาวอเมริกันเชื้อสายโปแลนด์ ซึ่งมักวิพากษ์วิจารณ์และท้าทายทฤษฎีต่าง ๆ ของไอน์สไตน์อยู่บ่อยครั้ง
ข้อความที่ไอน์สไตน์เขียนตอบซิลเบอร์สไตน์ ได้เอ่ยถึงสมการที่คนทั้งโลกรู้จักกันดีว่า “คำถามของคุณสามารถหาคำตอบได้จากสูตร E=mc²
ลักษณะทั่วไปเชิงสัมพัทธภาพ
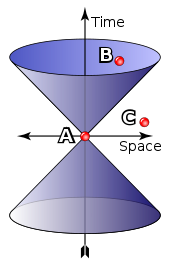
กรวยไฟ
ความโน้มถ่วงทางเรขาคณิตของนิวตันอาจเป็นเรื่องที่น่าสนใจ พื้นฐานของกลศาสตร์คลาสสิกเป็นเพียงกรณีจำกัดของกลศาสตร์สัมพัทธภาพ (พิเศษ) [30]ในภาษาของสมมาตร : ที่ซึ่งแรงโน้มถ่วงสามารถละเลยได้ ฟิสิกส์คือค่าคงที่ของลอเรนซ์เช่นเดียวกับในทฤษฎีสัมพัทธภาพพิเศษมากกว่าค่าคงที่กาลิเลอีเหมือนในกลศาสตร์คลาสสิก (ความสมมาตรที่กำหนดของทฤษฎีสัมพัทธภาพพิเศษคือกลุ่ม Poincaréซึ่งรวมถึงการแปล การหมุน และการเพิ่ม) ความแตกต่างระหว่างทั้งสองมีนัยสำคัญเมื่อต้องรับมือกับความเร็วที่เข้าใกล้ความเร็วของแสงและปรากฏการณ์พลังงานสูง [31]
ด้วยความสมมาตรของ Lorentz โครงสร้างเพิ่มเติมจึงเข้ามามีบทบาท ถูกกำหนดโดยชุดของโคนแสง (ดูรูป) กรวยแสงกำหนดโครงสร้างเชิงสาเหตุ: สำหรับแต่ละเหตุการณ์ Aมีชุดของเหตุการณ์ที่โดยหลักการแล้วสามารถมีอิทธิพลหรือได้รับอิทธิพลจากAผ่านสัญญาณหรือปฏิสัมพันธ์ที่ไม่จำเป็นต้องเดินทางเร็วกว่าแสง (เช่นเหตุการณ์Bในภาพ) และชุดของเหตุการณ์ที่อิทธิพลดังกล่าวเป็นไปไม่ได้ (เช่น เหตุการณ์Cในภาพ) ชุดเหล่านี้ไม่ขึ้นกับผู้สังเกต [32]ร่วมกับเส้นโลกของอนุภาคที่ตกลงมาอย่างอิสระ กรวยแสงสามารถใช้เพื่อสร้างเมตริกกึ่งรีมันเนียนของกาลอวกาศขึ้นใหม่ อย่างน้อยก็ขึ้นอยู่กับปัจจัยสเกลาร์ที่เป็นบวก ในแง่คณิตศาสตร์ สิ่งนี้กำหนดโครงสร้างตามรูปแบบ[33]หรือเรขาคณิตตามรูปแบบ
ทฤษฎีสัมพัทธภาพพิเศษถูกกำหนดในกรณีที่ไม่มีแรงโน้มถ่วง สำหรับการใช้งานจริง มันคือโมเดลที่เหมาะสมเมื่อใดก็ตามที่สามารถละเลยแรงโน้มถ่วงได้ นำเข้าสู่การเล่นแรงโน้มถ่วงและสมมติว่าเป็นสากลของการเคลื่อนไหวฤดูใบไม้ร่วงฟรีซึ่งเป็นเหตุผลที่คล้ายคลึงกับในส่วนก่อนหน้านี้มีผลบังคับใช้: ไม่มีโลกกรอบเฉื่อย แต่มีเฟรมเฉื่อยโดยประมาณเคลื่อนที่เคียงข้างอนุภาคที่ตกลงมาอย่างอิสระ แปลเป็นภาษาของกาลอวกาศ: เส้นตรงที่เหมือนเวลาซึ่งกำหนดกรอบเฉื่อยที่ปราศจากแรงโน้มถ่วงจะเปลี่ยนรูปเป็นเส้นที่โค้งสัมพันธ์กัน ซึ่งบ่งชี้ว่าการรวมของแรงโน้มถ่วงทำให้เกิดการเปลี่ยนแปลงในเรขาคณิตของกาลอวกาศ [34]
ในเบื้องต้น ยังไม่เป็นที่แน่ชัดว่าเฟรมท้องถิ่นใหม่ของการตกอย่างอิสระนั้นตรงกับกรอบอ้างอิงซึ่งมีกฎสัมพัทธภาพพิเศษอยู่หรือไม่—ทฤษฎีนั้นมีพื้นฐานมาจากการแผ่ขยายของแสง และด้วยเหตุนี้เกี่ยวกับแม่เหล็กไฟฟ้า ซึ่งอาจมีเซตที่แตกต่างกัน ของเฟรมที่ต้องการ แต่ด้วยการใช้สมมติฐานที่แตกต่างกันเกี่ยวกับเฟรมที่มีความสัมพันธ์พิเศษ (เช่น การยึดกับพื้นโลก หรือการตกอย่างอิสระ) เราสามารถคาดการณ์การเปลี่ยนแปลงของความโน้มถ่วงที่ต่างกันออกไป นั่นคือวิธีที่ความถี่ของแสงเปลี่ยนตามแสง แพร่กระจายผ่านสนามโน้มถ่วง (cf. ด้านล่าง ) การวัดจริงแสดงให้เห็นว่าเฟรมที่ตกลงมาอย่างอิสระคือเฟรมที่แสงแพร่กระจายเช่นเดียวกับในทฤษฎีสัมพัทธภาพพิเศษ [35]การวางนัยทั่วไปของคำกล่าวนี้ กล่าวคือกฎของสัมพัทธภาพพิเศษถือการประมาณที่ดีในกรอบอ้างอิงที่ตกลงมาอย่างอิสระ (และไม่หมุน) เรียกว่าหลักการสมมูลของไอน์สไตน์ซึ่งเป็นหลักการชี้นำที่สำคัญสำหรับการสรุปฟิสิกส์เชิงสัมพัทธภาพพิเศษ รวมถึงแรงโน้มถ่วง (36)
ข้อมูลการทดลองเดียวกันแสดงให้เห็นว่าเวลาที่วัดโดยนาฬิกาในสนามโน้มถ่วง — เวลาที่เหมาะสม , เพื่อให้คำศัพท์ทางเทคนิค — ไม่เป็นไปตามกฎของทฤษฎีสัมพัทธภาพพิเศษ ในภาษาของเรขาคณิตกาลอวกาศก็ไม่ได้วัดจากตัวชี้วัดคอฟสกี เช่นเดียวกับในกรณีของนิวตัน นี่เป็นการชี้นำถึงเรขาคณิตทั่วไปมากกว่า ในระดับขนาดเล็ก กรอบอ้างอิงทั้งหมดที่อยู่ในช่วงตกอย่างอิสระจะเทียบเท่ากัน และประมาณว่า Minkowskian ดังนั้นตอนนี้เรากำลังจัดการกับภาพรวมของพื้นที่ Minkowski ที่โค้งมน เมตริกซ์ตัวชี้วัดที่กำหนดรูปทรงเรขาคณิตในโดยเฉพาะอย่างยิ่งวิธีการที่มีความยาวและมุมวัด-ไม่ได้เป็นตัวชี้วัดคอฟสกีของสัมพัทธภาพพิเศษก็เป็นลักษณะทั่วไปที่รู้จักกันเป็นกึ่งหรือหลอกรีมันเมตริก นอกจากนี้ ตัวชี้วัด Riemannian แต่ละอันมีความสัมพันธ์ตามธรรมชาติกับการเชื่อมต่อประเภทใดประเภทหนึ่งโดยเฉพาะ การเชื่อมต่อLevi-Civitaและนี่คือการเชื่อมต่อที่เป็นไปตามหลักการความเท่าเทียมกันและทำให้พื้นที่ Minkowskian ในพื้นที่ (นั่นคือในพิกัดเฉื่อยที่เหมาะสมในท้องถิ่น , เมตริกคือ Minkowskian และอนุพันธ์บางส่วนแรกและค่าสัมประสิทธิ์การเชื่อมต่อจะหายไป
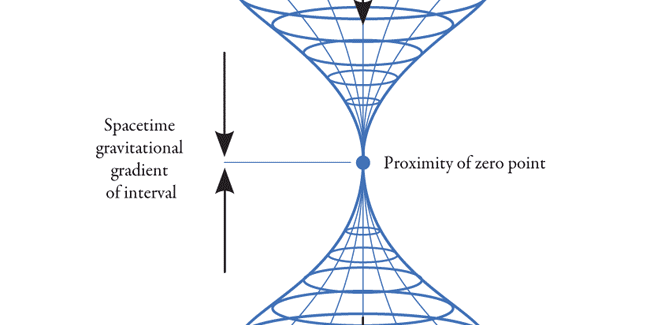
สมการสนามของรูหนอน
รูหนอนอวกาศ กับสมการสนามของไอน์สไตน์
ในการเข้าใจคอนเซปท์ของ Wormhole เราต้องเข้าใจถึงสมการสนามของไอน์สไตน์ ที่อาจอธิบายโดยคร่าวๆว่า เมตริกซ์ความโค้งของกาลอวกาศจะเท่ากับเมตริกซ์ของมวลและพลังงาน ในสภาพหลุมดำ มวลที่มีความหนาแน่นเกินขอบเขต รัศมีของซวาสไชลด์ทำให้ความโค้งของกาลอวกาศมีความชันจนหักลงสู่หลุมดำทั้งหมด แสงที่เดินทางตามระนาบอวกาศก็ย่อมจะตกลงตามความโค้งของกาลอวกาศนั้นไปด้วย ส่วน Wormhole ความโค้งของกาลอวกาศจะต้องอยู่ได้ด้วยตัวเองโดยไม่มีมวลและพลังงานมาเกี่ยวข้อง และเป็นการเขียนสมการข้างเดียวให้เมตริกซ์ของความโค้งสมมุลในตัวมันเองโดยไม่มีมวลและพลังงานมาทำให้ความโค้งของกาลอวกาศนั้นเสถียร สมการหลุมหนอน จึงมักถูกเรียกว่า Vacuum solution of Einstein equation คำตอบแบบสุญญากาศในสมการของไอน์สไตน์
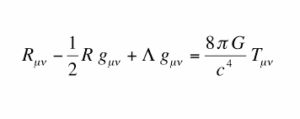
ถ้าพูดในทางวิทยาศาสตร์แบบเข้มๆ เราจะไม่พูดว่า สมการของไอน์สไตน์ทำนายการมีอยู่ของรูหนอน แต่เราจะพูดว่า สมการของไอน์สไตน์ไม่ได้ห้ามการมีอยู่ของหลุมหนอน แม้ว่า มันจะไม่เสถียร หรือจะเสถียรได้เมื่อรูเปิดมีขนาดเป็นจุด และอย่างใหญ่สุดไม่กี่ Planck length (1.616 x 10-35 m)
ขอบคุณข้อมูล https://www.bbc.com/
https://hmong.in.th/
และ https://www.scimath.org/