ประพจน์และการเชื่อมประพจน์-ตรรกศาสตร์เบื้องต้น
1. ประพจน์
ตัวอย่างประโยคที่เป็นประพจน์
ดาวอังคารเป็นดาวเคราะห์ (จริง)
จังหวัดลพบุรีไม่อยู่ทางภาคใต้ของประเทศไทย (จริง)
5 ≠ 8 (จริง)
19 + 4 ≠ 23 (เท็จ)
π เป็นจำนวนตรรกยะ (เท็จ)
ประโยคที่ไม่เป็นประพจน์
ได้แก่ ข้อความที่อยู่ในรูปของ คำถาม คำสั่ง คำขอร้อง คำอุทาน คำอ้อนวอน คำแสดงความปรารถนา สุภาษิตคำพังเพย ประโยคเปิด เพราะข้อความดังกล่าวไม่สามารถบอกค่าความจริงได้
ตัวอย่างประโยคที่ไม่เป็นประพจน์
คำถาม เช่น 3 หารด้วย 2 มีค่าเท่าไร
คำสั่ง เช่น จงยืนขึ้น
คำขอร้อง เช่น ช่วยกันรักษาความสะอาด
คำอ้อนวอน เช่น โปรดเมตตาด้วยเถิด
คำแสดงความปรารถนา เช่น อยากเห็นหน้าเธออีกสักครั้ง
คำอุทาน เช่น โอ้ย
สุภาษิตคำพังเพย เช่น วัวหายล้อมคอก
ประโยคเปิด เช่น เขาเป็นนักกีฬา
2. การเชื่อมประพจน์
ถ้าให้ p และ q เป็นประพจน์ เมื่อนำประพจน์มาเชื่อมกันด้วยตัวเชื่อมแล้ว เราเรัยกประพจน์ใหม่ว่า ประพจน์เชิงประกอบ ซึ่งตัวเชื่อมที่ใช้จะมี 5 ตัว คือ
5) ตัวเชื่อม นิเสธ ใช้สัญลักษณ์แทนด้วย ” ~ “
เรานิยมใช้สัญลักษณ์ p,q,r,s หรือตัวอักษรอื่นๆ แทนประพจน์
ข้อสังเกต ประโยคที่จะเป็นประพจน์จะต้องไม่กำกวม ต้องตอบได้ว่าเป็นจริงหรือเท็จ
ข้อความที่เป็นประพจน์
เช่น
10-2 = 4
พระอาทิตย์ขึ้นทางทิศตะวันตก
½ เป็นจำนวนตรรกยะ
เชียงใหม่เป็นจังหวัดหนึ่งของภาคเหนือ
1 ไม่เป็นจำนวนจริง
จะเห็นว่าประโยคข้างต้น เราสามารถบอกได้ว่าเป็นจริงหรือเท็จ ข้อความที่ไม่เป็นประพจน์ คือข้อความที่อยู่ในรูปคำอุทาน, คำถาม หรือข้อความที่บอกไม่ได้ว่าจริงหรือเท็จ
การเชื่อมประพจน์
กำหนดให้ p และ q เป็นประพจน์ใดๆ
1.) p∧q อ่านว่า p และ q มีค่าความจริงเป็นจริงแค่กรณีเดียว คือ p และ q มีค่าความจริงเป็นจริงทั้งคู่
เช่น p : กรุงเทพมหานครอยู่ในประเทศไทย
q : เชียงใหม่อยู่ในประเทศไทย
ดังนั้น p∧q มีค่าความจริงเป็นจริง เพราะ p มีค่าความจริงเป็นจริง และ q มีค่าความจริงเป็นจริง
Trick!! ประพจน์ที่เชื่อมกันด้วย “และ” ถ้าเป็นเท็จ(F)แค่อันเดียว ก็ถือว่าประพจน์นั้นเป็นเท็จ
2.) p∨q อ่านว่า p หรือ q มีค่าความจริงเป็นเท็จแค่กรณีเดียว คือ ทั้งp และq มีค่าความจริงเป็นเท็จทั้งคู่
ถ้ามองให้เห็นภาพง่ายขึ้น เราจะยกตัวอย่างสิ่งที่เห็นในขีวิตประจำวันบ่อยๆ คือคุณสมบัติการสมัครงาน
วุฒิการศึกษาที่ต้องการ : วิทยาศาสตรบัณฑิต สาขา คณิตศาสตร์ หรือ สาขาสถิติ
สรุปและตัวอย่างการเชื่อมประพจน์
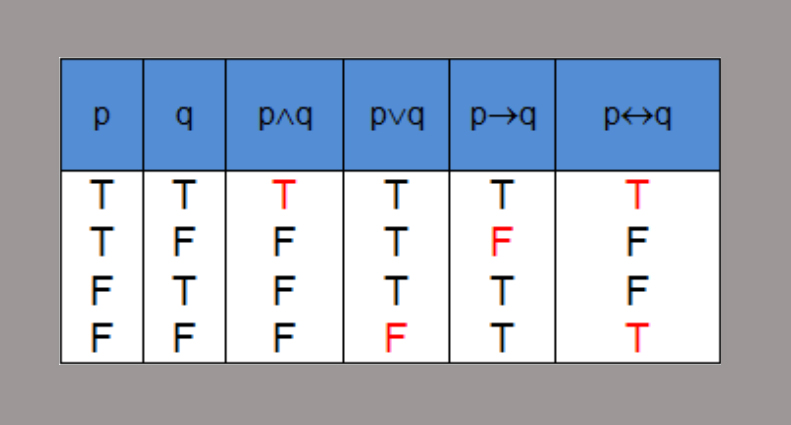
ในวิชาคณิตศาสตร์หรือในชีวิตประจำวัน จะพบประโยคที่ได้จากการเชื่อมประโยคอื่นๆ ด้วยคำว่า “และ” “หรือ” “ถ้า…แล้ว…” “ก็ต่อเมื่อ” หรือพบประโยคซึ่งเปลี่ยนแปลงมาจากประโยคเดิมโดยเติมคำว่า “ไม่” คำเหล่านี้เรียกว่าตัวเชื่อม (connectives) เช่น
2 และ 4 เป็นจำนวนคู่
ถ้า 3 เป็นจำนวนคี่ แล้ว เป็นจำนวนคี่
รูปสามเหลี่ยม ABC จะเป็นรูปสามเหลี่ยมด้านเท่า ก็ต่อเมื่อ รูปสามเหลี่ยม ABC มีด้านยาวเท่ากันทุกด้าน
เพื่อความสะดวกในการศึกษาเกี่ยวกับการเชื่อประพจน์ จะใช้อักษรภาษาอังกฤษตัวพิมพ์เล็ก เช่น p, q, r, s, … แทนประพจน์ที่นำมาเชื่อมกัน ค่าความจริงของประพจน์ที่มีตัวเชื่อมย่อมขึ้นอยู่กับจำนวนประพจน์ที่นำมาเชื่อมกันซึ่งสามารถพิจารณาค่าความจริงที่เป็นไปได้ทั้งหมด โดยใช้ T แทนจริง และ F แทนเท็จ ได้ดังนี้
ถ้ามีประพจน์เดียวกัน คือ p จะมีกรณีเกี่ยวกับค่าความจริงที่เกิดขึ้นได้ 2 กรณี คือ T หรือ F
(1) การเชื่อมประพจน์ด้วยตัวเชื่อม “และ”
พิจารณาประพจน์ 1+2 = 2+1
3 x 2 = 2×3
เมื่อเชื่อมประพจน์ทั้งสองด้วย “และ” จะได้ประพจน์ใหม่ คือ
1+2 = 2+1 และ 3×2 = 2×3
ในการเชื่อมประพจน์ด้วย “และ” มีข้อตกลงว่าประพจน์ใหม่ที่เป็นจริงในกรณีที่ประพจน์ที่นำมาเชื่อมกันนั้นเป็นจริงทั้งคู่ กรณีอื่นๆเป็นเท็จทุกกรณี
ถ้า p และ q เป็นประพจน์ ประพจน์ใหม่ที่ได้จากการเชื่อม p กับ q ด้วย “และ” คือ “p และ q “ เขียนแทนด้วย p ∧ q และตารางค่าความจริง (truth table) ของ p ∧ q เขียนได้ดังต่อไปนี้

จากตารางค่าความจริงข้างต้น เมื่อต้องการหาค่าความจริงของประพจน์ที่มีตัวเชื่อม “และ” ก็เพียงแต่ใช้ความรู้คณิตศาสตร์ พิจารณาค่าความจริงของประพจน์ที่นำมาเชื่อมว่าตรงกับกรณีใด เช่น
ต้องการหาค่าความจริงของ 3 Î {1, 3, 5, …} และ 3 เป็นจำนวนคี่
จะต้องพิจารณาค่าความจริงของ “3 Î {1, 3, 5, …}” และ “3 เป็นจำนวนคี่” ซึ่งเห็นได้ไม่ยากว่ามีค่าความจริงเป็นจริงทั้งคู่ ฉะนั้น ค่าความจริงของ 3 Î {1, 3, 5, …} และ 3 เป็นจำนวนคี่ คือ จริง
ในทำนองเดียวกัน ค่าความจริงของ เป็นจำนวนจริง และ เป็นจำนวนตรรกยะ คือ เท็จ เพราะประพจน์ เป็นจำนวนตรรกยะ มีค่าความจริงเป็นเท็จ
(2) การเชื่อมประพจน์ด้วยตัวเชื่อม “หรือ”
พิจารณาประพจน์ 1+5 = 5+1
4(2+3) = (4×2)+(4×3)
เมื่อเชื่อมประพจน์ทั้งสองด้วย “หรือ” จะได้ประพจน์ใหม่คือ
1+5 = 5+1 หรือ 4(2+3) = (4×2)+(4×3)
ในการเชื่อมประพจน์ด้วย “หรือ” มีข้อตกลงว่าประพจน์ใหม่จะเป็นเท็จในกรณีที่ประพจน์ที่นำมาเชื่อมกันเป็นเท็จทั้งคู่ กรณีอื่นๆเป็นจริงทุกกรณี
ถ้า p และ q เป็นประพจน์ ประพจน์ใหม่ที่ได้จากการเชื่อมด้วย “หรือ” คือ “p หรือ q” เขียนแทนด้วย pVq และตารางค่าความจริงของ pVq เขียนได้ดังนี้

1) “ เป็นจำนวนตรรกยะ หรือ เป็นจำนวนเต็ม” มีค่าความจริงเป็นเท็จ เพราะ เป็นจำนวนจริงที่ไม่ใช่จำนวนตรรกยะและไม่ใช่จำนวนเต็มจากตารางสรุปได้ว่า
2) “2 เป็นจำนวนคู่ หรือ เป็นจำนวนคี่” มีค่าความจริงเป็นจริง เพราะค่าความจริงของ “2 เป็นจำนวนคู่” คือ จริง
หมายเหตุ ความหมายของคำว่า “หรือ” ที่ใช้โดยทั่วไปมีสองกรณี
กรณีที่ 1 หมายถึง อย่างใดอย่างหนึ่งเท่านั้น เช่น ในการโยนเหรียญครั้งละ 1 เหรียญต่ละครั้งเหรียญจะขึ้นหัวหรือก้อยเพียงอย่างเดียว
กรณีที่ 2 หมายถึง อย่างใดอย่างหนึ่งหรือทั้งสองอย่าง เช่น ครูให้รางวัลแก่นักเรียนที่เรียนดีหรือช่วยกิจกรรมของโรงเรียน นักเรียนที่ได้รับรางวัลบางคนอาจเรียนดีเพียงอย่างเดียว บางคนอาจช่วยกิจกรรมของโรงเรียนเพียงอย่างเดียวแต่บางคนอาจมีคุณสมบัติทั้งสองประการก็ได้
ในตรรกศาสตร์มีข้อตกลงว่า ตัวเชื่อม “หรือ” หมายถึงกรณีที่ 2 เว้นแต่ว่าจะรพบุไว้อย่างชัดเจนให้หมายถึงกรณีที่
(3) การเชื่อมประพจน์ด้วยตัวเชื่อม “ถ้า…แล้ว…”
พิจารณาประพจน์ 2+3 = 3+2
6(2+3) = 6(3+2)
เมื่อเชื่อมด้วย “ถ้า…แล้ว…” ประพจน์ใหม่ที่เกิดขึ้น คือ
ถ้า 2+3 = 3+2 แล้ว 6(2+3) = 6(3+2)
ประพจน์ซึ่งตามหลังคำว่า ถ้า เรียกว่า เหตุ ส่วนประพจน์ซึ่งตามหลังคำว่า แล้ว เรียกว่า ผล
ในการเชื่อมประพจน์ด้วย “ถ้า…แล้ว…” มีข้อตกลงว่า ประพจน์ใหม่จะเป็นเท็จในกรณีที่เหตุเป็นจริงและผลเป็นเท็จเท่านั้น กรณีอื่นๆเป็นจริงทุกกรณี
ถ้า p และ q เป็นประพจน์ ประพจน์ใหม่ที่ได้จากการเชื่อมด้วย “ถ้า…แล้ว…” คือ “ถ้า p แล้ว q “ เขียนแทนด้วย p→q และตารางค่าความจริงของ p→q เขียนได้ดังนี้

1) ประพจน์ “ถ้า 0 เป็นจำนวนเต็ม แล้ว 0 เป็นจำนวนเต็มลบ” มีค่าความจริงเป็นเท็จเพราะบางประพจน์ “0 เป็นจำนวนเต็ม” และ “0 เป็นจำนวนเต็มลบ” มีค่าความจริงเป็นจริง และเท็จตามลำดับจากตารางและความรู้พื้นฐานทางคณิตศาสตร์ จะพบว่า
2) ประพจน์ “ถ้า 5 เป็นจำนวนคี่ แล้ว เป็นจำนวนคี่” มีค่าความจริงเป็นจริงเพราะประพจน์ “5 เป็นจำนวนคี่” และ “ เป็นจำนวนคี่” มีค่าความจริงเป็นจริงทั้งคู่
(4) การเชื่อมประพจน์ด้วยตัวเชื่อม “ก็ต่อเมื่อ”
การเชื่อมประพจน์ด้วยตัวเชื่อม “ก็ต่อเมื่อ” มีข้อตกลงว่า ประพจน์ใหม่จะเป็นจริงในกรณีที่ประพจน์ที่นำมาเชื่อมกันนั้นเป็นจริงด้วยกันทั้งคู่หรือเท็จด้วยกันทั้งคู่เท่านั้น กรณีอื่นๆเป็นเท็จเสมอ
ถ้า p และ q เป็นประพจน์ ประพจน์ใหม่ที่ได้จากการเชื่อมด้วย “ก็ต่อเมื่อ” คือ “p ก็ต่อเมื่อ q” เขียนแทนด้วย p↔ q และตารางค่าความจริงของ p↔q เขียนได้ดังนี้
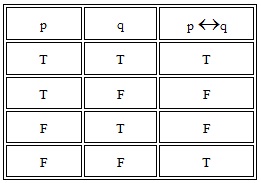
1) ประพจน์ “7 หารด้วย 2 ลงตัว ก็ต่อเมื่อ 7 เป็นจำนวนคู่” มีค่าความจริงเป็นจริงเพราะทั้งประพจน์ “7 เป็นจำนวนคู่” มีค่าความจริงเป็นเท็จทั้งคู่ จากตารางหาค่าความจริงของประพจน์ที่เชื่อมด้วยตัวเชื่อมก็ต่อเมื่อได้ดังตัวอย่าง
2) ประพจน์ “ = ก็ต่อเมื่อ 2 = -2 “ มีค่าความจริงเป็นเท็จ เพราะประพจน์ “2 < 3” และ “ > ” มีค่าความจริงเป็นจริง แต่ประพจน์ “2 = -2 “ มีค่าความจริงเป็นเท็จ
3) ประพจน์ “ 2 < 3 ก็ต่อเมื่อ“ > ” มีค่าความจริงเป็นจริง เพราะประพจน์ “ 2 < 3 ก็ต่อเมื่อ“ > ” มีค่าความเป็นจริงทั้งคู่
หมายเหตุ ข้อความทางคณิตศาสตร์ที่เป็นบทนิยามต่างๆ ถ้านำมาเขียนเป็นประโยคที่มีตัวเชื่อมจะมีความหมายเดียวกับการใช้ตัวเชื่อม “ก็ต่อเมื่อ”
(5) นิเสธของประพจน์
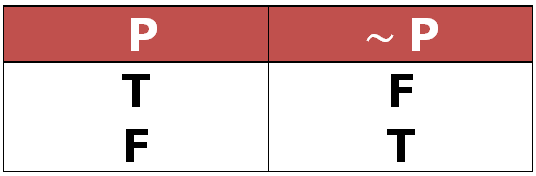
นิเสธของประพจน์ p เขียนแทนด้วย ~p และตารางค่าความจริงของ ~p เขียนได้ดังนี้
| p | ~p |
| T | F |
| F | T |
การพิจารณาค่าความจริงของประพจน์ที่เป็นนิเสธของประพจน์เดิมทำได้ง่ายที่สุด เพราะค่าความจริงของนิเสธจะเป็นค่าตรงข้ามกับค่าความจริงของประพจน์เดิมเสมอ
ข้อสังเกต
1) การเชื่อมประพจน์ด้วยตัวเชื่อม และ ” ∧ ” จะเป็น T เมื่อ p และ q เป็น T ทั้งคู่
2) การเชื่อมประพจน์ด้วยตัวเชื่อม หรือ ” ∨ ” จะเป็น F เมื่อ p และ q เป็น F ทั้งคู่
3) การเชื่อมประพจน์ด้วยตัวเชื่อม ถ้า… แล้ว… ” → ” จะเป็น F เมื่อ p เป็น T และ q เป็น F
4) การเชื่อมประพจน์ด้วยตัวเชื่อม ก็ต่อเมื่อ ” ↔ ” จะเป็น T เมื่อ p และ q มีค่าความจริงตรงกัน
3. การสร้างตารางค่าความจริง
กำหนด p , q , r เป็นประพจน์ที่ไม่ได้กำหนดค่าความจริงมาให้ จะเรียกประพจน์ที่มีตัวเชื่อมว่า รูปแบบประพจน์ เช่น ~p , p ∧ q , p → q , ( p ∨ q ) ↔ r เป้นต้น
ในการหาค่าความจริงของรูปแบบประพจน์ จะต้องพิจารณาค่าความจริงที่เป็นไปได้ของประพจน์ย่อยทุกกรณี โดยการสร้างตารางค่าความจริง
จำนวนกรณีที่พิจารณา = 2n กรณี
เมื่อ n คือ จำนวนประพจน์ย่อยของรูปแบบประพจน์นั้น
4. ประพจน์ที่สมมูลกัน
ประพจน์สองประพจน์ใด จะสมมูลกันก็ต่อเมื่อประพจน์ทั้งสองมีค่าความจริงเหมือนกันทุกกรณี ใช้สัญลักษณ์ ≡ แทนคำว่า สมมูล ประพจน์ที่สมมูลกันจะสามารถใช้แทนกันได้ เนื่องจากมีค่าความจริงเหมือนกันทุกกรณี
การตรวจสอบว่าประพจน์สมมูลกันหรือไม่ ทำได้ 2 วิธี ดังนี้
4.1 ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้สมมูลกันหรือไม่
1. p → q กับ ~p ∨ q
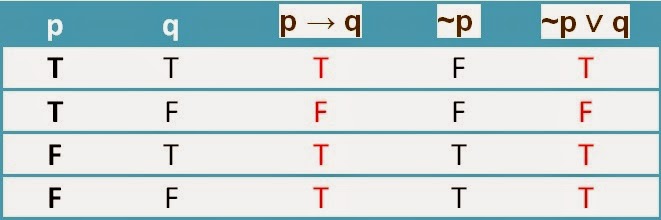
จะเห็นว่า ค่าความจริงของ p → q กับ ~p ∨ q ตรงกันกรณีต่อกรณี
ดังนั้น p → q สมมูลกับ ~p ∨ q
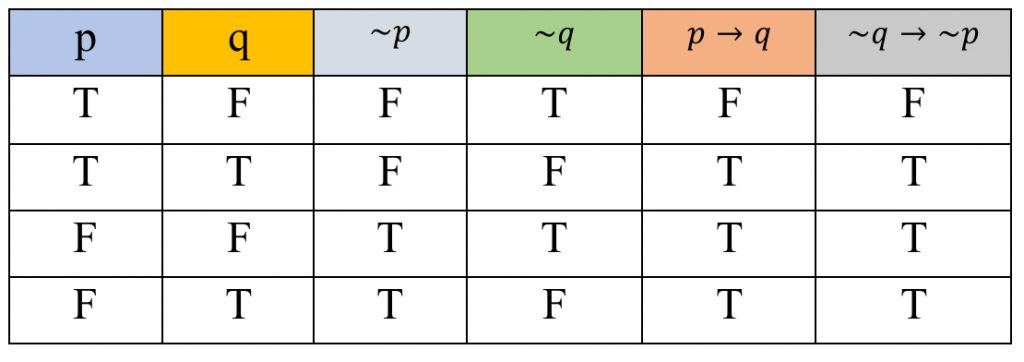
2. ~p ∧ q กับ p → q
จะเห็นว่า ค่าความจริงของ ~p ∧ q กับ p → q มีบางกรณีต่างกัน
ดังนั้น ~p ∧ q ไม่สมมูลกับ p → q