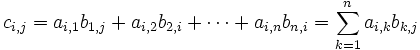การคูณสเกลาร์-เมทริกซ์

การคูณด้วยสเกลาร์

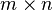กำหนดเมทริกซ์ $A = (a_{i,j})_{m \times n}$ และจำนวน c เราสามารถนิยาม ผลคูณสเกลาร์ cA ว่าเป็นเมทริกซ์ขนาด $m \times n$ ที่คำนวณโดยการนำ c ไปคูณสมาชิกแต่ละตัวของ A กล่าวคือ หาก $B = (b_{i,j})_{m \times n} = cA$ แล้ว b_i,j = ca_i,j ยกตัวอย่างเช่น

จะเห็นว่า ปฏิบัติการทั้งสองข้างต้น (การบวกและการคูณด้วยสเกลาร์) ช่วยให้เราสามารถมองเมทริกซ์ขนาด 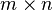$m \times n$ ว่าเป็นเวกเตอร์ที่มีมิติ mn ด้วยเหตุนี้ เซตของเมทริกซ์ที่มีขนาดเท่ากับจึงเป็นปริภูมิเวกเตอร์ชนิดหนึ่ง

การคูณ

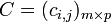ถ้า $A = (a_{i,j})_{m \times n}$ และ $B = (b_{i,j})_{n \times p}$ เป็นเมทริกซ์สองเมทริกซ์โดยที่จำนวนหลักของ A เท่ากับจำนวนแถวของ B แล้ว เราสามารถนิยาม ผลคูณ AB ว่าเป็นเมทริกซ์ $C = (c_{i,j})_{m \times p}$ โดยที่

$c_{i,j} = a_{i,1} b_{1,j} + a_{i,2} b_{2,i} + \cdots + a_{i,n} b_{n,i} = \sum_{k=1}^n a_{i,k} b_{k,j}$

กล่าวคือสมาชิกในแถว i หลัก j ของผลคูณ AB คำนวณได้จากการนำสมาชิกของหลัก i ของ A และสมาชิกของคอลัมน์ B ในตำแหน่ง “เดียวกัน” มาคูณกัน แล้วนำผลคูณทั้ง n ผลคูณนั้นมาบวกกัน

การคูณเมทริกซ์มีสมบัติต่อไปนี้

สมบัติการเปลี่ยนหมู่: (AB)C = A(BC) สำหรับเมทริกซ์ A ขนาด 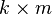$k \times m$ , B ขนาด 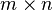$m \times n$ , และ C ขนาด $n \times p$ ใดๆ (“สมบัติการเปลี่ยนหมู่”)
สมบัติการแจกแจงทางขวา: (A + B)C = AC + BC สำหรับเมทริกซ์ A และ B ขนาด 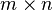$m \times n$ และ C ขนาด $n \times p$ ใดๆ
สมบัติการแจกแจงทางซ้าย: C(A + B) = CA + CB สำหรับเมทริกซ์ A และ B ขนาด 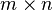$m \times n$ และ C ขนาด 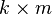$k \times m$ ใดๆ

คำเตือน: การคูณเมทริกซ์นั้นไม่เหมือนกับการคูณจำนวนโดยทั่วไป เนื่องจากไม่มีสมบัติสลับที่ กล่าวคือ สำหรับเมทริกซ์ A ขนาด 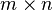$m \times n$ และ B ขนาด $n \times p$ ใดๆ

ถ้า $m \neq p$ แล้ว ผลคูณ BA ไม่มีนิยาม
แม้ m = p แต่ถ้า $m \neq n$ แล้ว AB เป็นเมทริกซ์ขนาด $m \times m$ ส่วน BA เป็นเมทริกซ์ขนาด $n \times n$ ผลคูณทั้งสองจึงมีค่าไม่เท่ากันอย่างเห็นได้ชัด
แม้ m = n = p แต่ส่วนมากแล้ว AB มักจะมีค่าไม่เท่ากับ BA ยกตัวอย่างเช่น

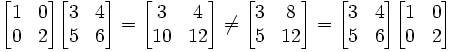
เรากล่าวว่าเมทริกซ์ A แอนติคอมมิวต์ (anticommute) กับเมทริกซ์ B ถ้า AB = − BA เมทริกซ์ที่แอนติคอมมิวต์ซึ่งกันและกันมีความสำคัญมากในการเป็นตัวแทนของพีชคณิตลีและพีชคณิตคลิฟฟอร์ด

ข้อสังเกตุ i = แถว หรือ row และ j = แถวตั้ง หรือ column

การคูณสเกลาร์-เมทริกซ์

การคูณ

Author: tmtyai

Related Posts