พื้นฐานคณิตศาสตร์-ฟังก์ชันเอกซ์โพเนนเชียล และฟังก์ชันลอการิทึม

ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการตั้งชื่อไม่เหมือนกัน ฟังก์ชันเอกซ์โพเนนเชียลก็เป็นอีกรูป

แบบหนึ่งของฟังก์ชันซึ่งเราจะไปดูว่าฟังก์ชันเอกซ์โพนเนนเชียลนั้นมีรูปแบบอย่างไร ก็ต้องไปดูนิยามของมันครับ ว่านิยามของฟังก์ชันเอกซ์โพเนนเชียลนั้นเป็นอย่างไร

นิยาม ฟังก์ชันเอ็กซ์โพเนนเชียลคือ ฟังก์ชัน f={(x,y)∈R×R+∣y=ax,a>0,a≠1}f={(x,y)∈R×R+∣y=ax,a>0,a≠1}

จากบทนิยามของฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันนี้มีรูปแบบในรูปของเลขยกกำลัง โดยฐานของมันต้องมากกว่า 0 และฐานต้องไม่เป็น 1  ตัวอย่างของฟังก์ชันเอกซ์โพเนนเชียลเช่น

y=10xy=10x

y=(15)xy=(15)x

y=(sin30∘)xy=(sin⁡30∘)x

y=(2–√)xy=(2)x

ตัวอย่างข้างต้นเป็นตัวอย่างของฟังก์ชันเอกซ์โพเนนเชียลครับ ซึ่งมีมากมายครับ นี่เป็นแค่ส่วนหนี่งเท่านั้นครับ

ต่อไปเราลองมาพิจารณาตัวอย่างต่อไปนี้ครับ

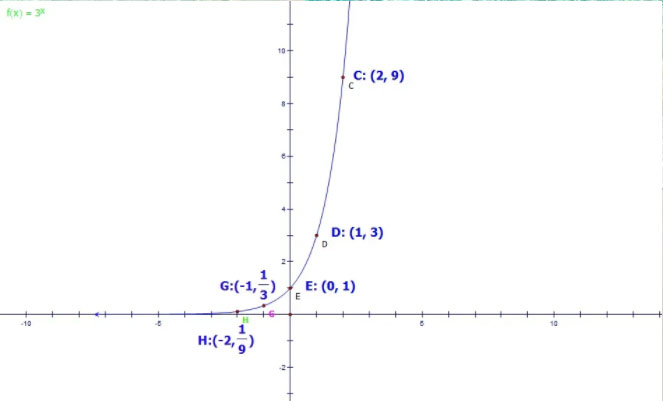
ตัวอย่างที่ 1 จงเขียนกราฟของฟังก์ชัน y=3xy=3x

การที่เราจะเขียนกราฟได้เราต้องกำหนดค่า x ขึ้นมาก่อน แล้วหาค่า y ครับ ดังนี้

ถ้า x=−2x=−2 จะได้

จาก y=3xy=3x แทน x ด้วย -2 ได้ว่า

y=3−2y=3−2

y=132y=132

y=19y=19

นั่นคือ ถ้า x=−2x=−2 ได้ว่า y=19y=19

ถ้า x=−1x=−1 จะได้

จาก  y=3xy=3x แทน x ด้วย -1 ได้ว่า

y=3−1y=3−1

y=131y=131

y=13y=13

นั่นคือ ถ้า x=−1x=−1 ได้ว่า y=13y=13

ถ้า x=0x=0 จะได้

จาก  y=3xy=3x แทน x ด้วย 0 ได้ว่า

y=30y=30

y=1y=1

นั่นคือ ถ้า x=0x=0 ได้ว่า y=1y=1

ถ้า x=1x=1 จะได้

จาก  y=3xy=3x แทน x ด้วย 1 ได้ว่า

y=31y=31

y=3y=3

นั่นคือ ถ้า x=1x=1 ได้ว่า y=3y=3

ถ้า x=2x=2 จะได้

จาก  y=3xy=3x แทน x ด้วย 2 ได้ว่า

y=32y=32

y=9y=9

นั่นคือ ถ้า x=2x=2 ได้ว่า y=9y=9

นำค่า x และค่า y ที่ได้มาเขียนลงในตารางเพื่่อเตรียนการพลอตกราฟขึ้นมาครับ

xx	−2−2	−1−1	00	11	22
yy	1919	1313	11	33	99

จากตารางจะได้คู่อันดับ

(−2,19),(−1,13),(0,1),(1,3),(2,9)(−2,19),(−1,13),(0,1),(1,3),(2,9)

กราฟคู่อันดับ

ฟังก์ชันลอการิทึม

ฟังก์ชันลอการิทึม คือฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล จากที่ฟังก์ชันเอกซ์โพเนนเชียลคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์ที่ส่งจากจำนวนจริงไปยังจำนวนจริงบวก โดยที่ ดังนั้นฟังก์ชันดังกล่าวซึ่งเป็นฟังก์ชันผกผันของเอกซ์โพเนนเชียล ก็คือ คู่อันดับ (y, x)  หรืออาจจะบอกได้อีกแบบคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์จากจำนวนจริงบวกไปยังจำนวนจริง โดยที่  จัดรูปใหม่ ได้เป็น  (อ่านว่าล็อก x ฐาน a)

บทนิยาม

logarithm คือฟังก์ชันที่อยู่ในรูป {(x, y) ∈  :   } โดยที่ a เป็นจำนวนจริงที่มากกว่า 0 และ a ≠ 1

ตัวอย่าง 

จัดรูปเป็น      อ่านว่า ล็อก x ฐาน 5

กราฟคู่อันดับ