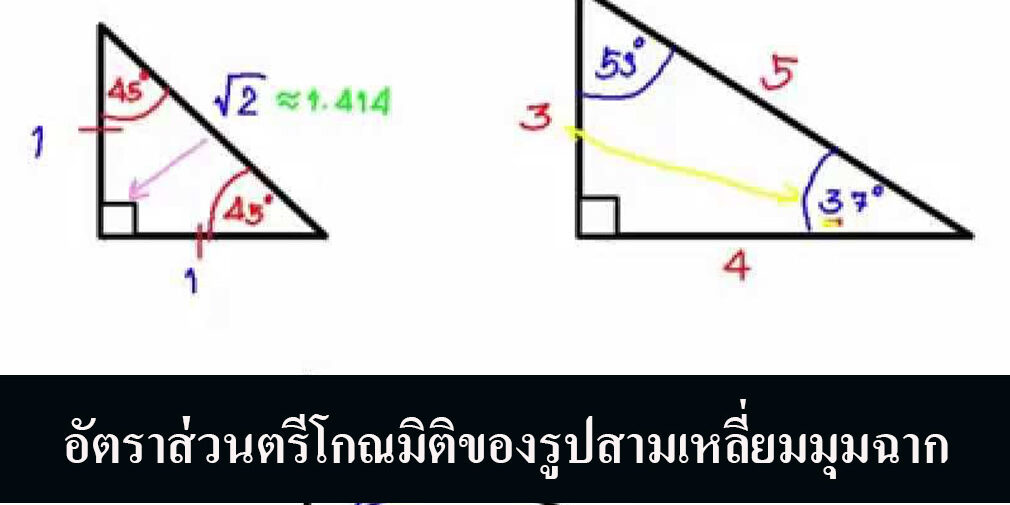
ตรีโกณมิติ (Trigonometry) มาจากรากศัพท์ภาษากรีก 2 ค า คือ trigonon หมายถึง มุม 3 มุม และ metro หมายถึง การวัดในภาษาไทย ตรีโกณมิติมาจากค าว่า ตรี(แปลว่า สาม)
โกณ (แปลว่า มุมหรือเหลี่ยม) มิติ (แปลว่า การวัด) ดังนั้น ตรีโกณมิติ หรือ Trigonometry จึงหมายถึง การวัดและหาความสัมพันธ์ระหว่าง
ด้าน มุม และพื้นที่ของรูปสามเหลี่ยม อัตราส่วนตรีโกณมิติ (Trigonometric Ratio) หมายถึง อัตราส่วนของความยาวด้าน ทั้งสามของรูปสามเหลี่ยมมุมฉาก
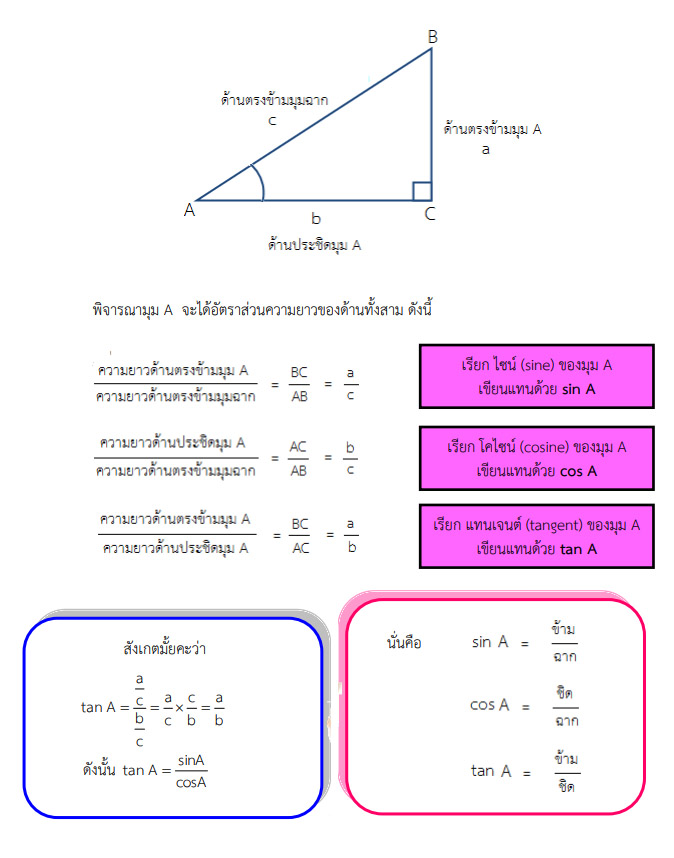
จากรูป ABC เป็นรูปสามเหลี่ยมมุมฉาก มี ACB เป็นมุมฉาก
ถ้า พิจารณามุม A จะได้ว่า
1. ด้าน AB เรียก ด้านตรงข้ามมุมฉาก ยาว c หน่วย
2. ด้าน BC เรียก ด้านตรงข้ามมุม A ยาว a หน่วย
3. ด้าน AC เรียก ด้านประชิดมุม A ยาว b หน่วย
ความหมายอัตราส่วนตรีโกณมิติ
อัตราส่วนตรีโกณมิติ
อัตราส่วนตรีโกณมิติ (Trigonometric Ratio) หมายถึง อัตราส่วนของด้านของรูปสามเหลี่ยมมุมฉาก การเรียนในเรื่องนี้ผู้เรียนจำเป็นต้อง ใช้ความรู้เดิมเรื่องสามเหลี่ยมคล้ายเพื่อเป็นพื้นฐานในการทำความเข้าใจ การเรียนวิชาตรีโกณมิติให้ได้ดีนั้นต้องจำนิยามของตรีโกณมิติให้ได้ ระดับมัธยมต้นใช้นิยามสามเหลี่ยมมุมฉาก ซึ่งอัตราส่วนตรีโกณมิติ ก็คือ อัตราส่วนของความยาวด้านสองด้านของสามเหลี่ยมมุมฉากซึ่งจะมีชื่อเรียกดังนี้
“Sine A” ไซน์ของมุม A หรือเขียนย่อว่า sin A หาได้จากอัตราส่วนของความยาวด้านตรงข้ามมุม A ต่อความยาวด้านตรงข้ามมุมฉาก
“Cos A” โคไซน์ของมุม A หรือเขียนย่อว่า cos A หาได้จากอัตราส่วนของความยาวด้านประชิดมุม A ต่อความยาวด้านตรงข้ามมุมฉาก
“Tangent A” แทนเจนต์ของมุม A หรือเขียนย่อว่า tan A หาได้จากอัตราส่วนของความยาวด้านตรงข้ามมุม A ต่อความยาวด้านประชิดมุม A
ส่วนฟังก์ชัน cosec, sec และ cot นั้น ก็ใช้นิยามเข้าช่วย ซึ่งเป็นส่วนกลับของ sin, cos และ tan ตามลำดับ จึงต้องจำฟังก์ชัน sin, cos, tan ก็จะได้ในส่วนของ cosec, sec และ cot ขึ้นมาเองโดยอัตโนมัติ
“Cotangent A” โคแทนเจนต์ของมุม A หรือเขียนย่อว่า cot A หาได้จากอัตราส่วนของความยาวด้านด้านประชิดมุม A ต่อความยาวด้านตรงข้ามมุม A
“Secant A” ซีแคนต์ของมุม A หรือเขียนย่อว่า sec A หาได้จากอัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อ ความยาวด้านประชิดมุม A
“Cosecant A” โคซีแคนต์ของมุม A หรือเขียนย่อว่า cosec A หาได้จากอัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อ ความยาวด้านตรงข้ามมุม A
นิยามจากรูปสามเหลี่ยมมุมฉาก


รูปสามเหลี่ยมมุมฉากจะมีมุมหนึ่งมีขนาด 90° (π/2 เรเดียน) ในที่นี้คือ C ส่วนมุม A กับ B นั้นเปลี่ยนแปลงได้ ฟังก์ชันตรีโกณมิติกำหนดความสัมพันธ์ระหว่างความยาวด้านและมุมภายในรูปสาม เหลี่ยมมุมฉากในการนิยามฟังก์ชันตรีโกณมิติสำหรับมุม A เราจะกำหนดให้มุมใดมุมหนึ่งในรูปสามเหลี่ยมมุมฉากเป็นมุม A เรียกชื่อด้านแต่ละด้านของรูปสามเหลี่ยมตามนี้
- ด้านตรงข้ามมุมฉาก (hypotenuse) คือด้านที่อยู่ตรงข้ามมุมฉาก หรือเป็นด้านที่ยาวที่สุดของรูปสามเหลี่ยมมุมฉาก ในที่นี้คือ h
- ด้านตรงข้าม (opposite side) คือด้านที่อยู่ตรงข้ามมุมที่เราสนใจ ในที่นี้คือ a
- ด้านประชิด (adjacent side) คือด้านที่อยู่ติดกับมุมที่เราสนใจและมุมฉาก ในที่นี้คือ b
จะได้
1). ไซน์ ของมุม คือ อัตราส่วนของความยาวด้านตรงข้าม ต่อความยาวด้านตรงข้ามมุมฉาก ในที่นี้คือ
sin(A) = ข้าม/ฉาก = a/h
2). โคไซน์ ของมุม คือ อัตราส่วนของความยาวด้านประชิด ต่อความยาวด้านตรงข้ามมุมฉาก ในที่นี้คือ
cos(A) = ชิด/ฉาก = b/h
3). แทนเจนต์ ของมุม คือ อัตราส่วนของความยาวด้านตรงข้าม ต่อความยาวด้านประชิด ในที่นี้คือ
tan(A) = ข้าม/ชิด = a/b
4). โคซีแคนต์ csc(A) คือฟังก์ชันผกผันการคูณของ sin(A) นั่นคือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านตรงข้าม
csc(A) = ฉาก/ข้าม = h/a
5). ซีแคนต์ sec(A) คือฟังก์ชันผกผันการคูณของ cos(A) นั่นคือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านประชิด
sec(A) = ฉาก/ชิด = h/b
6). โคแทนเจนต์ cot(A) คือฟังก์ชันผกผันการคูณของ tan(A) นั่นคือ อัตราส่วนของความยาวด้านประชิด ต่อความยาวด้านตรงข้าม
cot(A) = ชิด/ข้าม = b/a
วิธีจำ
วิธีจำอย่างง่าย ๆ คือจำว่า ข้ามฉาก ชิดฉาก ข้ามชิด ซึ่งหมายความว่า
-
- ข้ามฉาก … sin = ด้านตรงข้าม/ด้านตรงข้ามมุมฉาก
- ชิดฉาก … cos = ด้านประชิด/ด้านตรงข้ามมุมฉาก
- ข้ามชิด … tan = ด้านตรงข้าม/ด้านประชิด