ตรรกศาสตร์เบื้องต้น – การตรวจสอบการสมมูลกันโดยการสร้างตารางค่าความจริง
การสร้างตารางค่าความจริง
กำหนด p , q , r เป็นประพจน์ที่ไม่ได้กำหนดค่าความจริงมาให้ จะเรียกประพจน์ที่มีตัวเชื่อมว่า รูปแบบประพจน์ เช่น ~p , p ∧ q , p → q , ( p ∨ q ) ↔ r เป้นต้น
ในการหาค่าความจริงของรูปแบบประพจน์ จะต้องพิจารณาค่าความจริงที่เป็นไปได้ของประพจน์ย่อยทุกกรณี โดยการสร้างตารางค่าความจริง
จำนวนกรณีที่พิจารณา = 2n กรณี
เมื่อ n คือ จำนวนประพจน์ย่อยของรูปแบบประพจน์นั้น
ในการตรวจสอบการสมมูลนั้นเราจะใช้วิธีการสร้างตารางค่าความจริงของทั้งสองประพจน์เพื่อเปรียบเทียบค่าความจริงในทุกกรณี
เช่น
ตรวจสอบการสมมูลโดยการสร้างตารางค่าความจริง
p∧(q∨r) สมมูลกับ (p∧q)∨(p∧r) หรือไม่
จากสองประพจน์ที่กำหนดให้ มีประพจน์ย่อยทั้งหมด 3 ประพจน์ ดังนั้น มีกรณีทั้งหมด 23=8 ประพจน์
สร้างตารางค่าความจริงของ p∧(q∨r) จะได้

ประพจน์ที่สมมูลกัน
ประพจน์สองประพจน์ใด จะสมมูลกันก็ต่อเมื่อประพจน์ทั้งสองมีค่าความจริงเหมือนกันทุกกรณี ใช้สัญลักษณ์ ≡ แทนคำว่า สมมูล ประพจน์ที่สมมูลกันจะสามารถใช้แทนกันได้ เนื่องจากมีค่าความจริงเหมือนกันทุกกรณี
การตรวจสอบว่าประพจน์สมมูลกันหรือไม่ ทำได้ 2 วิธี ดังนี้
4.1 ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้สมมูลกันหรือไม่
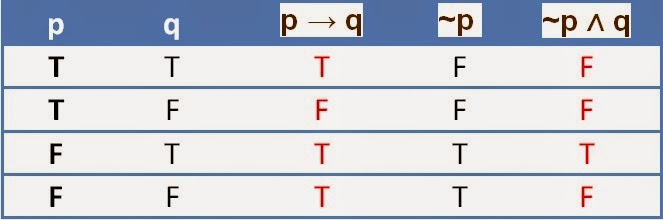
1. p → q กับ ~p ∨ q

จะเห็นว่า ค่าความจริงของ ~p ∧ q กับ p → q มีบางกรณีต่างกัน
ดังนั้น ~p ∧ q ไม่สมมูลกับ p → q
4.2 ใช้รูปแบบของประพจน์ที่สมมูลกัน
รูปแบบของประพจน์ที่สมมูลกันที่สำคัญ
1. p ∧ ~p ≡ F
2. p ∨ ~p ≡ T
3. p ∧ T ≡ p
4. p ∨ F ≡ p
5. ~(~p) ≡ p
6. p ∨ q ≡ q ∨ p
7. p ∧ q ≡ q ∧ p
8. ( p ∨ q ) ∨ r ≡ p ∨ ( q ∨ r ) ≡ p ∨ q ∨ r
9. ( p ∧ q ) ∧ r ≡ p ∧ ( q ∧ r ) ≡ p ∧ q ∧ r
10. p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r )
11. p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r )
12. ~( p ∨ q ) ≡ ~p ∧ ~q
13. ~( p ∧ q ) ≡ ~p ∨ ~q
14. p → q ≡ ~q → ~p
15. p → q ≡ ~p ∨ q
16. ~( p → q ) ≡ p ∧ ~q
17. p ↔ q ≡ ( p → q ) ∧ ( q → p )
รูปแบบของประพจน์ที่สมมูลกัน
ในวิชาตรรกศาสตร์ ถ้ารูปแบบของประพจน์สองรูปแบบใดมีค่าความจริงตรงกันกรณีต่อกรณี แล้วจะสามารถนำไปใช้แทนกันได้ เรียกสองรูปแบบของประพจน์ดังกล่าวว่าเป็น รูปแบบประพจน์ที่สมมูลกัน เช่น – p → q กับ ~p q เป็นรูปแบบที่สมมูลกัน ซึ่งแสดงการตรวจสอบความสมมูลได้ดังนี้
|
p |
q | p → q | ~p | ~p q |
| T
T F F |
T
F T F |
T
F T T |
F
F T T |
T F T T |
จะเห็นว่า ค่าความจริงของ p → q กับ ~p q ตรงกันกรณีต่อกรณี
| ตัวอย่างที่ 1 | กำหนดให้ p และ q เป็นประพจน์ จงตรวจสอบ ~(p q) สมมูลกับ ~p Λ ~q หรือไม่ |
| วิธีทำ | สร้างตารางค่าความจริงของ ~(p q) กับ ~p Λ ~q ดังนี้ | ||||||||||||||
|
|||||||||||||||
| จะเห็นว่า ค่าความจริงของ ~(p q) กับ ~p Λ ~q ตรงกันกรณีต่อกรณี | |||||||||||||||
| ดังนั้น ~(p q) สมมูลกับ ~p Λ ~q |
| ตัวอย่างที่ 2 | กำหนดให้ p และ q เป็นประพจน์ จงตรวจสอบว่า p → q สมมูลกับ ~q → ~p หรือไม่ |
| วิธีทำ | สร้างตารางค่าความจริงของ p → q กับ ~q → ~p ดังนี้ | ||||||||||||
|
|||||||||||||
| จะเห็นว่า ค่าความจริงของ p → q กับ ~q → ~p ตรงกันกรณีต่อกรณี | |||||||||||||
| ดังนั้น p → q สมมูลกับ ~q → ~p |
| ตัวอย่างที่ 3 | กำหนดให้ p และ q เป็นประพจน์ จงตรวจสอบว่า ~p Λ q สมมูลกับ p → q หรือไม่ |
| วิธีทำ | สร้างตารางค่าความจริงของ ~p Λ q กับ p → q ดังนี้ | ||||||||||
|
|||||||||||
| จะเห็นว่า ค่าความจริงของ ~p Λ q กับ p → q มีบางกรณีที่ต่างกัน | |||||||||||
| ดังนั้น ~p Λ q ไม่สมมูลกับ p → q |
| ตัวอย่างที่ 4 | กำหนดให้ p และ q เป็นประพจน์ จงตรวจสอบว่า (p → q) Λ (q → p) สมมูลกับ p ↔ q หรือไม่ |
| วิธีทำ | สร้างตารางค่าความจริงของ (p → q) Λ (q → p) กับ p ↔ q ดังนี้ | ||||||||||||
|
|||||||||||||
| จะเห็นว่า ค่าความจริงของ (p → q) Λ (q → p) กับ p ↔ q ตรงกันกรณีต่อกรณี | |||||||||||||
| ดังนั้น (p → q) Λ (q → p) สมมูลกับ p ↔ q |
ข้อความสองข้อความจะสมมูลกันหรือไม่ สามารถตรวจสอบได้โดยเปลี่ยนข้อความเป็นสัญลักษณ์ในรูปแบบของประพจน์ แล้วพิจารณาว่ารูปแบบของประพจน์ทั้งสองสมมูลกันหรือไม่ ดังตัวอย่างต่อไปนี้
| ตัวอย่างที่ 5 | จงตรวจสอบว่าข้อความสองข้อความต่อไปนี้สมมูลกันหรือไม่ |
| “ถ้า 82 เป็นจำนวนคู่ แล้ว 8 เป็นจำนวนคู่” | |
| “ถ้า 8 ไม่เป็นจำนวนคู่ แล้ว 82 ไม่เป็นจำนวนคู่” |
| วิธีทำ | ให้ | p | แทน | 82 | เป็นจำนวนคู่ |
| q | แทน | 8 | เป็นจำนวนคู่ | ||
| ดังนั้น p → q แทน ถ้า 82 เป็นจำนวนคู่แล้ว 8 เป็นจำนวนคู่ | |||||
| และ ~q → ~p แทน ถ้า 8 ไม่เป็นจำนวนคู่แล้ว 82 ไม่เป็นจำนวนคู่ | |||||
| จากตัวอย่างที่ 2 ได้ตรวจสอบแล้วพบว่า p → q สมมูลกับ ~q → ~p | |||||
| ดังนั้น ข้อความทั้งสองข้างต้นจึงสมมูลกัน | |||||
รูปแบบของประพจน์ที่สมมูลกันมีประโยชน์มากในการพิสูจน์ทฤษฎีบทต่างๆ ในวิชาคณิตศาสตร์ เช่น ถ้ามีข้อความในรูปแบบ p → q อาจเปลี่ยนข้อความนั้นใหม่ให้อยู่ในรูปแบบ ~p q หรือ ~q → ~p
ขอบคุณข้อมูล https://www.opendurian.com/






