ตรรกศาสตร์เบื้องต้น-เรื่องสัจนิรันดร์
ประพจน์ที่เป็นสัจนิรันดร์ คือ รูปแบบของประพจน์ที่มี ค่าความจริงเป็นจริงเสมอ ไม่ว่าประพจน์ย่อยจะมีค่าความจริงเป็น จริง หรือ เท็จ ก็ตาม เช่น p ∨ ~p , p → p , ~( p ∧ ~p ) , p ↔ p เป็นต้น
การตรวจสอบว่าประพจน์ใดเป็นสัจนิรันดร์ ทำได้ดังนี้
1. ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้ เป็นสัจนิรันดร์หรือไม่
1. [ ( p → q ) ∧ p ] → q
ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้ เป็นสัจนิรันดร์หรือไม่
1. [ ( p → q ) ∧ p ] → q

จะเห็นว่ารูปแบบของประพจน์ [ ( p → q ) ∧ p ] → q มีค่าจริงเป็นจริงทุกกรณี
ดังนั้น [ ( p → q ) ∧ p ] → q เป็น สัจนิรันดร์
2. ใช้วิธีการหาข้อขัดแย้ง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้ เป็นสัจนิรันดร์หรือไม่
1. ( p ∧ q ) → ( q ∨ p )
วิธีทำ สมมุติว่า ( p ∧ q ) → ( q ∨ p ) เป็นเท็จ
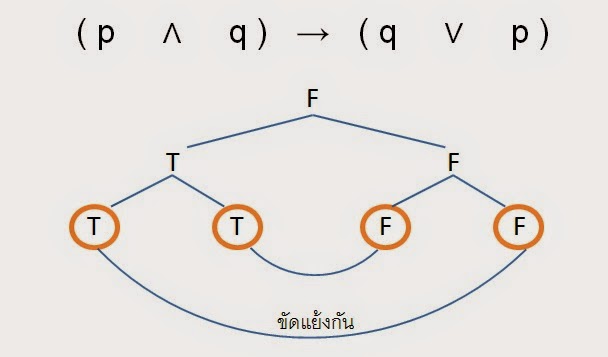
จากแผนภาพ จะเห็นว่า ค่าความจริงของ p และ q เป็นได้ทั้งจริงและเท็จ
แสดงว่าไม่มีกรณีที่ทำให้ ( p ∧ q ) → ( q ∨ p ) เป็นเท็จ
ดังนั้น รูปแบบของประพจน์ ( p ∧ q ) → ( q ∨ p ) เป็นสัจนิรันดร์
ตรวจสอบสัจนิรันดร์โดยการสมมุติให้เป็นเท็จ
หลักการการสมมุติให้เป็นเท็จ คือ การหาว่าเป็นไปได้มั้ยที่ประพจน์นั้นจะเป็นเท็จ ถ้ามีแม้แต่กรณีเดียวได้ค่าความจริงเป็นเท็จขึ้นมา แสดงว่าไม่เป็นสัจนิรันดร์ แต่ถ้า
เมื่อสมมุติให้เป็นเท็จแล้วเกิดการขัดแย้งขึ้นเสมอ หมายความว่า ประพจน์นั้นย่อมเป็นสัจนิรันดร์
การตรวจสอบสัจนิรันดร์โดยการสมมุติให้เป็นเท็จ
ประพจน์ [(p→q)∧(q→r)]→(p→r) เป็นสัจนิรันตร์หรือไม่
สมมุติให้ประพจน์ที่กำหนดให้เป็จเท็จ ดังนั้นเราจะต้องหาว่าตัวเชื่อมหลักของประพจน์นี้คืออะไร ซึ่งตัวเชื่อมหลักคือ
( (p → q) ∧ (q→ r) ) → ( p → r )
![]()
ดังนั้นเราจะกำหนดให้ → ที่วงกลมด้านบน มีค่าความจริงเป็นเท็จ จะได้
( (p → q) ∧ (q→ r) ) → ( p → r )
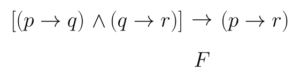
ตัวอย่าง 1 ประพจน์ [∼(p→q)]→[(∼p↔q)][∼(p→q)]→[(∼p↔q)] เป็นสัจนิรันดร์หรือไม่
วิธีทำ ใช้หลักการเดียวกันกับตัวอย่างแรก จะได้แผนภาพคือ
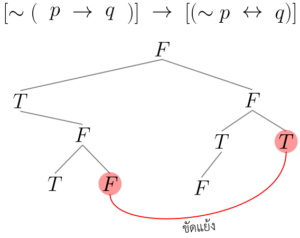
ตอบ ประพจน์ที่กำหนดให้เป็นสัจนิรันดร์
.
ตัวอย่าง 2 ประพจน์∼p∧(p∨∼(r∧s))]→(∼r∨s)∼p∧(p∨∼(r∧s))]→(∼r∨s)เป็นสัจนิรันดร์หรือไม่
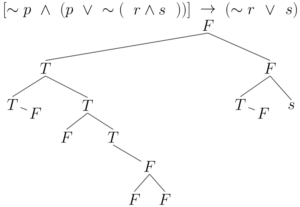
วิธีทำ วาดแผนภาพโดยใช้หลักการเดียวกับตัวอย่างข้อแรก จะได้
จากแผนภาพจะได้ว่า ไม่มีข้อขัดแย้งใด ๆ เกิดขึ้น แสดงว่า ประพจน์ที่กำหนดให้สามารถเกิดกรณีที่เป็นเท็จขึ้นได้ ดังนั้นประพจน์ที่กำหนดให้ไม่เป็นสัจนิรันดร์
ตอบ ประพจน์ ∼p∧(p∨(̸r∧s))]→(∼r∨s)∼p∧(p∨(̸r∧s))]→(∼r∨s) ไม่เป็นสัจนิรันดร์
ตัวอย่าง 3 ตรวจสอบสัจนิรันดร์ โดย การสร้างตารางค่าความจริง
ประพจน์ (p∨q)∧p(p∨q)∧p เป็นสัจนิรันดร์หรือไม่
จากประพจน์ที่กำหนดให้ จะมีประพจน์ย่อยทั้งหมดสองประพจน์ ดังนั้นสร้างตารางที่มีประพจน์สองประพจน์นี้ขึ้นมา
| p | q |
จากนั้นให้เติมกรณีที่เป็นไปได้ทั้งหมด ซึ่ง จำนวนกรณีที่เป็นไปได้ทั้งหมดคือ 2n เมื่อ n คือจำนวนประพจน์ วิธีการเติมที่ง่าย และ ได้ครบทุกกรณีโดยไม่ตกหล่น คือ การเติมแบบกลุ่มกลุ่มละครึ่ง
เช่น ในข้อนี้ มีประพจน์ทั้งหมด 2 ประพจน์ ดังนั้นจะมีทั้งหมด 22= 4 กรณี เริ่มแรก เนื่องจากมี 4 กรณี จะได้ว่าครึ่งหนึ่งคือ2 ดังนั้นหลักแรกให้เติม T จำนวนสองตัว และ F จำนวนสองตัว จะได้
| p | q |
| T | |
| T | |
| F | |
| F |
จากนั้นให้ ให้ดูครึ่งนึงของ 22 จะได้ 11 ดังนั้นในหลักที่ 22 ให้เติม TT กับ FF สลับกันครั้งละหนึ่งตัว จะได้
| p | q |
| T | T |
| T | F |
| F | T |
| F | F |
เราก็จะได้กรณีที่เป็นไปได้ครบทั้งหมด
จากโจทย์เราต้องการค่าความจริงของประพจน์ (p∨q)∧p(p∨q)∧p จากตารางข้างบนเราไม่มีค่าความจริงของ p∨qp∨q ดังนั้นสร้างหลักของ p∨qp∨q เพิ่ม และเติมค่าความจริงให้เรียบร้อย จะได้
| p | q | p∨q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
ตอนนี้เรามีค่าความจริงครบทั้งหมดแล้ว ดังนั้นให้สร้างหลักสุดท้าย เป็นหลักของ ประพจน์ที่เราต้องการตรวจสอบ จะได้
| p | q | p∨q | (p∨q)∧p |
| T | T | T | T |
| T | F | T | T |
| F | T | T | F |
| F | F | F | F |
จากตารางด้านบนจะเห็นว่ามีสองกรณีที่ค่าความจริงของประพจน์ที่โจย์ถามนั้นเป็นเท็จ จึง ทำให้ได้ว่า ประพจน์นี้ ไม่เป็นสัจนิรันดร์
ตอบ ประพจน์ที่กำหนดให้ ไม่เป็นสัจนิรันดร์
สรุป
| ประพจน์ที่เป็นสัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงเป็นจริง ทุกกรณีของประพจน์ย่อย | ||
| ตัวอย่างประพจน์ที่เป็นสัจนิรันดร์ที่ควรทราบ มีดังนี้ | ||
| p ∨ ~q | [ ~p ∧ ( p ∨ q)] → q | |
| ~(p ∧ ~q) | [ ( p → q) ∧ ~q ] → ~p | |
| (p ∧ q) → p | (p ∧ q) ⇔ (q ∧ p) | |
| (p ∧ q) → q | (p ∨ q) ⇔ (q ∨ p) | |
| p → (p ∨ q) | (p → q) ⇔ (~p ∨ q) | |
| q → (p ∨ q) | (p → q) ⇔ (~q → ~p) | |
| [ p ∧ ( p → q)] → q | (~p ∨ q) ⇔ (~q → ~p) | |
| [ ~p ∧ ( p → q)] → ~q | ( p ⇔ q) ⇔ [(p → q) ∧ (q → p)] | |
| ข้อสังเกต | ประพจน์ที่สมมูลกัน เมื่อนำมาเชื่อมด้วยตัวเชื่อม ⇔ จะได้ประพจน์ใหม่ซึ่งเป็นสัจนิรันดร์ นั่นคือ ถ้า A และ B สมมูลกันแล้ว A ⇔ B เป็นสัจนิรันดร์ | |






