คณิตศาสตร์ออนไลน์เรื่อง-ฟังก์ชันพหุนาม (Polynomial Function)

ฟังก์ชันพหุนาม

ให้ P(x) ฟังก์ชันพหุนามดีกรี n เขียนได้ในรูป

P(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ

เรียก a_i สำหรับ i = 1,2,3,…, n ว่าสัมประสิทธิ์ กรณีที่สัมประสิทธิ์นำ a_n = 1 เรียกพหุนามนี้ว่าพหุนามโมนิค ในหัวข้อนี้เราจะศึกษาเกี่ยวกับพหุนามโมนิค จากทฤษฎีมูลฐานของพีชคณิตเราจะพบว่า พหุนามดีกรี n นั้นจะประกอบด้วยรากจำนวน n รากในที่นี้แทนด้วย k1, k2, …, kn นั้นคือ

P(x) = (x – k1)(x – k2)…(x – kn)

ในกรณีที่รากเป็นจำนวนจริงเราจะได้ว่ากราฟพหุนามจะตัดแกน x จำนวน n ครั้งในกรณีที่ k1, k2,…, kn แตกต่างกันทั้งหมด แต่ในกรณีที่มีรากซ้ำเส้นกราฟจะตัดแกน x ที่ค่ารากเพียงครั้งเดียวซึ่งผู้เขียนจะยกตัวอย่างพหุนามกำลังสามประกอบตัวเพื่อความสะดวกจะพิจารณาพหุนามโมนิคที่มีค่ารากเป็นจำนวนเต็มซึ่งในกรณีที่รากเป็นจำนวนจำนวนจริงใด ๆ แนวคิดในการวิเคราะห์เป็นไปในทำนองเดียวกัน สมมติให้มีราก 3 รากประกอบด้วย k1, k2 และ k3 เราจะวิเคราะห์ประเภทกราฟจากการซ้ำของรากพหุนาม 3 กรณีคือ กรณีไม่มีรากซ้ำ {k1, k2, k3} , กรณีมีรากซ้ำ 1 ค่า { 2(k1), k2} , กรณีที่มีรากซ้ำกัน 3 ค่า {3(k1)}

หรือ

ฟังก์ชันพหุนามเป็นฟังก์ชั่นที่สามารถกำหนดโดยการประเมินพหุนาม อย่างแม่นยำยิ่งขึ้นฟังก์ชัน $f$ ของอาร์กิวเมนต์หนึ่งจากโดเมนที่กำหนดคือฟังก์ชันพหุนามหากมีพหุนาม

P(x) = a n x n + a n-1 x n-1 + \dots + a 2 x 2 + \dotsa 1 x+ a 0

ที่ประเมินเป็น $P(x)$ สำหรับทุก $x$ ในโดเมนของ $ฉ$ (ที่นี่, $n$ เป็นจำนวนเต็มไม่เป็นลบและ $0$ $,$ $1$ $,$ $2$ $, \dots ,$ $n$ มีค่าสัมประสิทธิ์คงที่) โดยทั่วไปเว้นแต่ระบุไว้ฟังก์ชั่นพหุนามมีความซับซ้อนสัมประสิทธิ์ข้อโต้แย้งและค่านิยม โดยเฉพาะอย่างยิ่งพหุนามซึ่งถูก จำกัด ให้มีสัมประสิทธิ์จริงกำหนดฟังก์ชันจากจำนวนเชิงซ้อนไปจนถึงจำนวนเชิงซ้อน หากโดเมนของฟังก์ชันนี้ถูก จำกัด ไว้ที่ค่าจริงฟังก์ชันที่ได้คือฟังก์ชันจริงที่แมปจริงกับค่าจริง

ตัวอย่างเช่นฟังก์ชัน $f$ กำหนดโดย

P (x) = x³−x

เป็นฟังก์ชันพหุนามของตัวแปรเดียว ฟังก์ชันพหุนามของตัวแปรหลายตัวถูกกำหนดไว้ในทำนองเดียวกันโดยใช้พหุนามในมากกว่าหนึ่งไม่แน่นอนเช่นเดียวกับใน

f(x,y)=2x^{3}+4x^{2}y+xy^{5}+y^{2}-7.

ตามนิยามของฟังก์ชันพหุนามอาจมีนิพจน์ที่เห็นได้ชัดว่าไม่ใช่พหุนาม แต่ยังคงกำหนดฟังก์ชันพหุนาม ตัวอย่างคือนิพจน์ $\left({\sqrt {1-x^{2}}}\right)^{2},$ ซึ่งรับค่าเดียวกันกับพหุนาม $1-x^{2}$ ในช่วงเวลา $[-1,1]$ ดังนั้นทั้งสองนิพจน์จึงกำหนดฟังก์ชันพหุนามเดียวกันในช่วงเวลานี้

ทุกฟังก์ชั่นพหุนามเป็นอย่างต่อเนื่อง , ราบรื่นและทั้งหมด

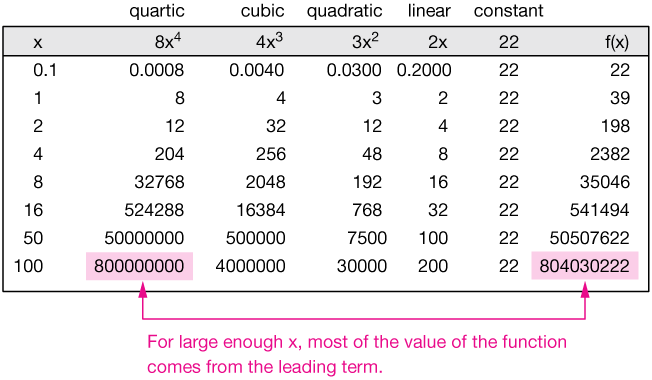
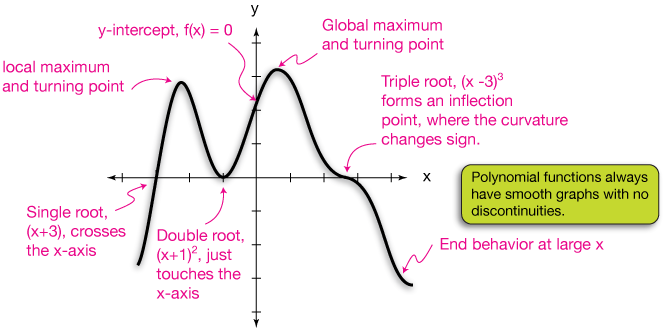
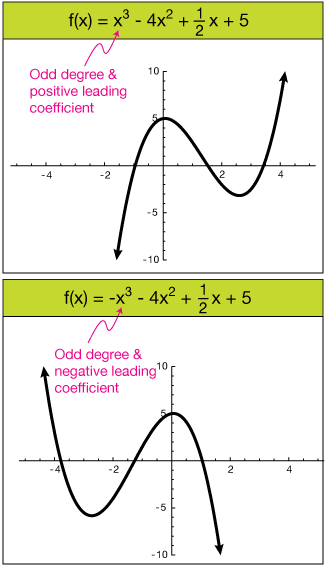
ตัวอย่างที่ พิจารณากราฟพหุนาม P(x) = (x-1)(x-1)(x+2) ในภาพที่ 21 พบว่าพหุนามมีรากแตกต่างกัน 2 ค่าและมีรากซ้ำ 1 ค่าคือ { -2, 2(1) } กราฟฟังก์ชันจึงตัดแกน x ที่จุด (-2,0) และ (1,0)

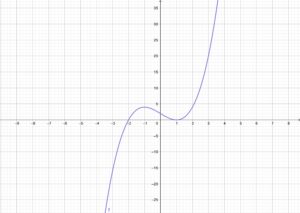
กราฟฟังก์ชัน P(x) = (x-1)(x-1)(x+2)

วิเคราะห์ค่าของฟังก์ชันตามโดเมนของฟังก์ชันจะพบว่าโดเมนถูกแบ่งออกเป็น 3 ส่วนคือ

P1 = (-infinity,-2), P2 = (-2,1), P3 = (1,infinity) พบว่า

ค่า x ที่อยู่ในช่วงของ P1 จะทำให้ค่าฟังก์ชันเป็นลบ

ค่า x ที่อยู่ในช่วงของ P2 จะทำให้ค่าฟังก์ชันเป็นบวก

ค่า x ที่อยู่ในช่วงของ P3 จะทำให้ค่าฟังก์ชันเป็นบวก

จากการสังเกตตำแหน่งค่าราก x = -2 พบว่าค่าฟังก์ชันทางด้านซ้ายและทางด้านขวามีเครื่องหมายที่แตกต่างกันแต่ ณ ตำแหน่งของ x = 1 ซึ่งเป็นรากซ้ำกลับพบว่าค่าฟังก์ชันทางด้านซ้ายและทางด้านขวามีเครื่องหมายเหมือนกัน

สูตรที่ใช้ในการแยกตัวประกอบ

ผลต่างกำลังสอง

น² – ล²= (น– ล)(น+ ล)

กำลังสองสมบูรณ์

(น + ล)² = น²+ 2นล +ล²