ความหมายของความน่าจะเป็น
ในชีวิตประจำวันของทุกคนต้องได้ยินคำว่า ความน่าจะเป็น หรือ โอกาส เช่น โอกาสที่วันนี้แดดจะออกมีมาก ความน่าจะเป็นที่โยนเหรียญแล้วจะได้หัว มีเท่ากับได้ก้อย หรือความน่าจะเป็นที่จะถูกหวย มาน้อยกว่าจะถูกเจ้ามือกิน ฯลฯ ในยุคสมัคยก่อนที่ผู้คนส่วนมากใช้ความรู้สึกหรืออารมณ์ในการตัดสินใจอะไรหลายๆอย่าง ซึ่งร้อยคนก็มีความเห็นไม่เหมือนกัน ไม่มีหลักการในการคิด ความน่าจะเป็นจึงมีใช้ช่วยในการตัดสินในเกี่ยวกับเหตุการณ์ต่าง ๆ ได้ถูกต้องมากขึ้น เช่น วันนี้ควรจะเตรียมร่มหรือเสื้อกันฝนเวลาออกนอกบ้าน หรือไม่เมื่อมองดูท้องฟ้าแล้วมืดครึ้ม แสดงว่าโอกาสที่ฝนจะตกวันนี้มีมาก ดังนั้นจึงควรเตรียมอุปกรณ์ที่จะกันฝนได้ไปด้วย อาจจะเป็นร่ม หรือเสื้อกันฝนก็ได้
นิยามของความน่าจะเป็น
ถ้าการทดลองอย่างสุ่มหนึ่ง มีสมาชิกของ แซมเปิลสเปซ เป็นจำนวนเท่ากับ N
และจำนวนสมาชิกของเหตุการณ์ E ที่เราสนใจ มีค่าเท่ากับ n
โดยที่แต่ละสมาชิกของแซมเปิลสเปซนั้น มีโอกาสเกิดขึ้นได้เท่าๆกัน
ความน่าจะเป็นของ การเกิดเหตุการณ์ E เขียนแทนด้วย P(E) จะมีค่าเท่ากับ n/N หรือ P(E)
นิยามของคำที่เกี่ยวข้อง
การที่เราจะเข้าใจเรื่องความน่าจะเป็นนั้นเราจะต้องทำความรู้จักคำศัพท์ต่างๆ เหล่านี้ก่อน ดังนั้นมาลุยกันเลย!
- Trial = การทดลอง หรือ การสังเกตการณ์ ซึ่งมักจะเป็นเหตุการณ์ที่เราไม่รู้แน่ชัดถึงผลลัพธ์ เช่น Trial คือการโยนเหรียญ การทอยลูกเต๋า การการดึงไพ่ เป็นต้น ซึ่งความน่าจะเป็นนั้นจะให้ความสนใจถึงผลลัพธ์ของ Trial นั้นๆ
- Sample Space (S) = ผลลัพธ์ทั้งหมดที่เป็นไปได้ของ Trial
เช่น การโยนเหรียญ ซึ่งหน้าเหรียญที่เป็นไปได้มี 2 แบบ คือ h=หัว, t= ก้อย- ถ้า Trial เป็นการโยนเหรียญ 1 ครั้ง S ={h,t} คือมีทั้งหมด 2 แบบ
- ถ้า Trail เป็นการโยนเหรียญ 2 ครั้ง S = {(h, h), (h, t), (t, h), (t, t)} ซึ่งจะมีทั้งหมด 4 แบบ
- Events (E) = เหตุการณ์ใน Sample Space ที่เราสนใจ เช่น เหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 ครั้ง ในการโยนเหรียญ 2 ครั้ง คือ E={(h, h), (h, t), (t, h)} ซึ่งเป็นไปได้ 3 แบบ
ดังนั้น ความน่าจะเป็นของสิ่งที่เราสนใจ จะเขียนได้ว่า
Probability of Event หรือ P(E) = จำนวน Event E / จำนวน Sample Space = E/S
- S = {(h, h), (h, t), (t, h), (t, t)} = 4 แบบ
- E = {(h, h), (h, t), (t, h)} = 3 แบบ
ดังนั้น P(ออกหัวอย่างน้อย 1 ครั้งในการโยนเหรียญ 2 ครั้ง) = 3/4 = 0.75 หรือ 75%
การคำนวนความน่าจะเป็น (หรือใช้กับกฎการนับก็ได้) เมื่อมีเหตุการณ์มากกว่า 1 เหตุการณ์
แบบเกิดอย่างน้อยเหตุการณ์ใดเหตุการณ์หนึ่ง (Union=OR)
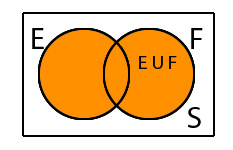
- หลักการคือเอาความน่าจะเป็นมารวมกัน แค่ว่าระวังว่าการรวมนั้นจะทำให้เบิ้ลหรือไม่ เช่น
- กรณีที่เหตุการณ์ทั้งสองอย่างไม่สามารถเกิดพร้อมกันได้ (เรียกว่า Mutually Exclusive)
- เมื่อไม่มีส่วนซ้ำ ก็จะบวกกันตรงๆ ได้เลย
- P (E U F) = P(E) + P(F)
- กรณีเหตุการณ์ทั้งสองอย่าง สามารถเกิดพร้อมกันได้
- เพราะ E และ F มีส่วนซ้ำกัน ทำให้ถ้าบวกตรงแล้วเราจะนับเบิ้ลไป 1 ที จึงต้องเอาส่วนที่ซ้ำกันออกไป 1 ที (ให้หายเบิ้ล)
- P (E U F) = P(E) + P(F) – P(E ∩ F)
- ซึ่งจะเห็นว่า ถ้าเป็น Mutually Exclusive แล้ว P(E ∩ F) จะเท่ากับ 0 ทำให้ได้สูตรข้างบนนั่นเอง
สเปซตัวอย่าง (Sample Space)
นิยาม 8.1 เซตของผลที่เป็นได้ทั้งหมดจากการทดลองจะเรียกว่า สเปซตัวอย่าง และเขียนแทนด้วยเซต
S ผลของการทดลองแต่ละแบบเรียกว่าเป็นสมาชิก (Element) หรือจุดตัวอย่าง (SamplePoint)
ตัวอย่างเช่น ในการโยนเหรียญ 1 เหรียญ
S = {H, T} โดยที่ H หมายถึง หัวและ T หมายถึง ก้อย
ในการโยนลูกเต๋า 1 ลูก ถ้าสนใจแต้มบนลูกเต๋า จะได้
S = {1, 2, 3, 4, 5, 6}
แต่ถ้า สนใจว่าเป็นแต้มคู่หรือคี่ จะได้
S = {คู่, คี่}
ในการทดลองท าข้อสอบปรนัย 3 ข้อถ้าสนใจว่าท าถูกหรือผิด จะได้
S = {TTT, TTF, TFT, FTT, FFT, FTF, TFF, FFF}
โดยที่ T หมายถึงท าข้อสอบถูกและ F หมายถึงท าข้อสอบผิด
แต่ถ้าสนใจจ านวนข้อที่ท าถูก จะได้
S = {0, 1, 2, 3}
ข้อสังเกต จะเห็นได้ว่าในการทดลองหนึ่งๆ สเปซตัวอย่างอาจมีได้หลายแบบ ทั้งนี้ขึ้นอยู่กับความ
สนใจผลของการทดลองว่าเป็นแบบใด
เหตุการณ์ (Events)
ในการทดลองนั้นบางครั้งสิ่งที่สนใจอาจเป็นแค่ผลของการทดลองบางส่วน จากผลที่เป็นไป
ได้ทั้งหมด ตัวอย่างเช่นในการโยนเหรียญ 3 เหรียญ ถ้าพิจารณาถึงจ านวนเหรียญที่ขึ้นหัว จะได้
ว่าสเปซ ตัวอย่าง S = {0, 1, 2, 3} แต่สิ่งที่สนใจ อาจเป็นแค่จ านวนเหรียญที่ขึ้นหัวไม่เกิน 1 เหรียญ เป็น
ต้น
นิยาม 8.2 เหตุการณ์ หมายถึง เซตย่อย (Subset) ของสเปซตัวอย่าง
ตัวอย่างเช่น ในการโยนลูกเต๋า 1 ลูก
สเปซตัวอย่าง S ={1, 2, 3, 4, 5, 6}
ถ้า E1 เป็นเหตุการณ์ที่แต้มบนลูกเต๋ามากกว่า 2จะได้ว่า
E1= {3, 4, 5, 6}
ถ้า E2
เป็นเหตุการณ์ที่แต้มบนลูกเต๋าเป็นเลขคี่จะได้ว่า
E2= {1, 3, 5}
นิยาม 8.3 ก าหนดสเปซตัวอย่าง S และก าหนดเหตุการณ์ A คอมพลีเมนต์ (Complement) ของ
เหตุการณ์ A เขียนแทนด้วย A’ หมายถึง เซตของสมาชิกของ S ที่ไม่ได้เป็นสมาชิกของเหตุการณ์A
นิยาม 8.4 ก าหนดสเปซตัวอย่าง S และกำหนดเหตุการณ์ A และ B ยูเนียน (Union) ของเหตุการณ์ A
และ B เขียนแทนด้วย A U B หมายถึงเซตของสมาชิกS ที่อยู่ใน A หรือ B
นิยาม 8.5 ก าหนดสเปซตัวอย่าง S และกำหนดเหตุการณ์ A และ B อินเตอร์เซคชัน (Intersection) ของ
เหตุการณ์ A และ B เขียนแทนด้วย A ∩ B หมายถึงเซตของสมาชิกS ที่อยู่ใน A และ B
ตัวอย่างเช่น กล่องใบหนึ่งมีสลากที่มีหมายเลขตั้งแต่ 1 – 20 อย่างละ 1 ใบ ถ้าหยิบสลาก 1 ใบจากกล่อง
ใบนี้ จะได้ว่า S = {1, 2, 3,…, 20}
ถ้า A เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 2 ลงตัว
B เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 3ลงตัว
จะได้ว่า A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
B = {3, 6, 9, 12, 15, 18}
A’ = เป็นเหตุการณ์ที่สลากนั้นมีหมายเลขที่หารด้วย 2 ไม่ลงตัว
A’ = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
Bayes’s Theorem เริ่มมีประโยชน์ในการเข้ามาช่วยครับ มันเจ๋งตรงที่มันใช้ความน่าจะเป็นในทิศกลับกันมาช่วยหาได้
ทฤษฎี
ทีนี้เรามาดูกันว่าเจ้า Bayes’s Theorem

เป็นสูตรที่ Make Sense พิจารณาจากความรู้เรื่อง Conditional Probability ที่ว่า
P(A ∩ B) = P(A) × P(B|A)
ดังนั้นสูตรข้างบนมันก็คือ
P(A | B) = P (A ∩ B) / P(B)หากพิจารณาจาก Venn Diagrams จะเข้าใจง่ายมาก ว่าทำไมสูตรถึงออกมาแบบนั้น
ซึ่งแปลว่า ความน่าจะเป็นของ A หลังจากเกิด B แล้ว เท่ากับ ความน่าจะเป็นของการเกิดทั้ง A และ B หารด้วย ความน่าจะเป็นของ B
ตัวอย่างที่ 1 อยากทราบว่าสามารถเรียงสับเปลี่ยน คำว่า “กนกวรรณ” ได้กี่เหตุการณ์
วิธีทำ ตัวอักษรมีทั้งหมด 7 ตัว เป็นอักษร ก. 2 ตัว อักษร น. 1 ตัว อักษร ว. 1 ตัว อักษร ร. 2 ตัวและอักษร ณ. 1 ตัว
ดังนั้นเหตุการณ์ที่เกิดขึ้น
= 7!
2!1!1!2!1
= (7×6×5×4×3)
2
=1260 เหตุการณ์
การเรียงสับเปลี่ยนแบบวงกลม คือ การเรียงลำดับเป็นวงกลมแบ่งออกได้เป็น 2 ลักษณะ คือ
ลักษณะที่ 1 การเรียงสับเปลี่ยนสิ่งของ n สิ่งที่ไม่เหมือนกันจะได้จำนวนเหตุการณ์เท่ากับ (n-1)! เหตุการณ์
แบบฝึกหัดบทที่ 3
1. ถุงผ้าใบหนึ่งมีลูกแก้วอยู่ 4 สี คือสีเหลือง 4 ลูก สีแดง 3 ลูก สีฟ้า 3 ลูก และสีเขียว 2 ลูก จงหา
1.1 ความน่าจะเป็นที่จะสุ่มหยิบมา 1 ลูกแล้วได้ลูกแก้วสีฟ้า
1.2 ความน่าจะเป็นที่จะสุ่มหยิบมา 2 ลูกแล้วได้ลูกที่ 1 เป็นสีเขียว และลูกที่ 2 เป็นสีแดง โดยการสุ่มหยิบขึ้นมา แล้วไม่นำลูกแก้วที่สุ่มขึ้นมาได้ใส่กลับเข้าไปในถุง
1.1 วิธีทำ P(E) = (n(E)) / (n(S))
สุ่มหยิบลูกแก้ว 1 ลูกแล้วได้สีฟ้า เนื่องจากลูกแก้วสีฟ้ามี 3 ลูก จะได้
n(E) = 3 เหตุการณ์มีลูกแก้วอยู่ 4 สี คือสีเหลือง 4 ลูก สีแดง 3 ลูก สีฟ้า 3 ลูก และสีเขียว 2 ลูก
ดังนั้น P(E) = 3/12 = 1/4 = 0.25
n(S) = 4 + 3 + 3 + 2 = 12 เหตุการณ์
ความน่าจะเป็นที่จะสุ่มหยิบมา 1 ลูกแล้วได้ลูกแก้วสีฟ้าเท่ากับ 0.25
1.2 วิธีทำ P(E) = (n(E)) / (n(S))
สุ่มหยิบลูกแก้ว 1 ลูก ให้ได้ลูกสีเขียวเป็นลูกแลกโดยไม่ใส่คืน จะได้ n(E)/n(S) = 2/12 = 0.16
สุ่มหยิบลูกแก้วอีก 1 ลูก ให้ได้ลูกสีแดงเป็นลูกที่สองโดยไม่ใส่คืน จะได้ n(E)/n(S) = 3/11 = 0.27
ดังนั้น ความน่าจะเป็นที่จะสุ่มหยิบลูก 2 ลูกแล้วได้ลูกที่ 1 เป็นสีเขียว และลูกที่ 2 เป็นสีแดงโดยไม่นำลูกแก้วที่สุ่มขึ้นมาได้ใส่กลับเข้าไปในถุงอีกจะได้ = 0.16 x 0.27 = 0.043
2. ในกล่องใบหนึ่งมีฉลากอยู่ 15 ใบ โดยแต่ละใบมีหมายเลขกำกับ คือ เลข 1 จำนวน 6 ใบ เลข 2 จำนวน 5
ใบ และเลข 3 จำนวน 4 ใบ จงหาความน่าจะเป็นที่สุ่มหยิบมา 1 ใบ แล้วได้หมายเลข 2 หรือ หมายเลข 3
วิธีทำ P(E) = (n(E)) / (n(S))
สุ่มหยิบมา 1 ใบ แล้วได้หมายเลข 2 จะได้ n(E) = 5 เหตุการณ์
สุ่มหยิบมา 1 ใบ แล้วได้หมายเลข 3 จะได้ n(E) = 4เหตุการณ์
n(E) = 5 + 4 = 9 เหตุการณ์
กล่องใบหนึ่งมีฉลากอยู่ 15 ใบ n(S) = 15
ดังนั้น ความน่าจะเป็นที่สุ่มหยิบมา 1 ใบ แล้วได้หมายเลข 2 หรือ หมายเลข 3 เท่ากับ 0.6
3. บริษัทแห่งหนึ่งมีลานจอดรถยนต์สำหรับพนักงานซึ่งจอดได้ 4 คัน เท่ากับจำนวนรถยนต์ของพนักงานโดยพนักงานแต่ละคนมีรถยนต์ยี่ห้อต่างกัน คือ ยี่ห้อโตโยต้า ยี่ห้อฮอนด้า ยี่ห้ออีซูซุ และยี่ห้อมิชซูบิชิ จงหาความน่าจะเป็นที่รถยนต์ยี่ห้อโตโยต้าจะจอดอยู่ริมขวาสุดของลานจอดรถ
วิธีทำ P(E) = (n(E)) / (n(S))
เหตุการณ์ที่รถยนต์ยี่ห้อโตโยต้า อยู่ฝั่งทางขวามือ
n(E) = 3! = 3 × 2 × 1 = 6 (มาจากการเรียงสับเปลี่ยนแนวเส้นตรง จากสูตร คือ n! และ n คือจำนวนที่สับเปลี่ยน)เหตุกาณ์ทั้งหมด
n(S) = 4! = 4 × 3 × 2 × 1 = 24
ดังนั้น P(E)=6/24=1/4=0.25






