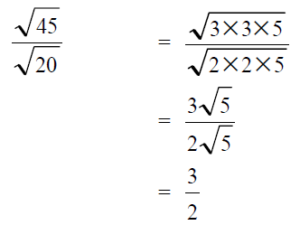การดำเนินการของจำนวนจริงซึ่งเกี่ยวกับกรณฑ์ที่สอง
สมบัติการสลับที่สำหรับการบวก
√a + √b = √b + √a
Ex. √5 + √2 = √2 + √5
สมบัติการเปลี่ยนหมู่สำหรับการบวก
( √a+ √b )+ √c = √a+( √b + √c )
Ex. ( √2+ √3 )+ √5 = √2+( √3 + √5 )
สมบัติการสลับที่สำหรับการคูณ
√a x √b = √b x √a
Ex. √5 x √3 = √3 x √5
สมบัติการเปลี่ยนหมู่สำหรับการคูณ
( √a x √b ) x √c = √a x ( √b x √c )
Ex. ( √7 x √11 ) x √13 = √7 x ( √11 x √13 )
สมบัติการแจกแจง
√a x ( √b +√c ) = ( √a x √b ) +( √a x √c )
( √b + √c ) x √a = ( √b x √a + √c x √a )
Ex. √2 x ( √3 +√5 ) = ( √2 x √3 ) +( √2 x √5 )
( √8 + √7 ) x √5 = ( √8 x √5 + √7 x √5 )
นิยามของกรณฑ์ที่สอง
เมื่อ a แทนจำนวนจริงบวกใด ๆ หรือ ศูนย์ รากที่สองของ a คือ จำนวนจริงบวกที่ยกกำลังสองแล้วเท่ากับ a รากที่สองของจำนวนบวกใด ๆ จะมีสองค่าเสมอ ส่วนรากที่สองของศูนย์เท่ากับศูนย์
สมบัติของกรณฑ์ที่สอง
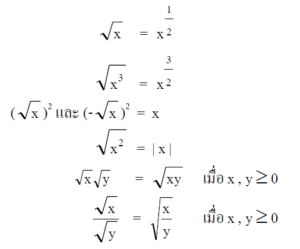
สมบัติการสลับที่การบวกและการสลับที่การคูณ
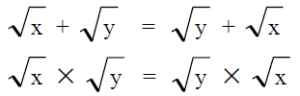
สมบัติการเปลี่ยนหมู่การบวกและการเปลี่ยนหมู่การคูณ
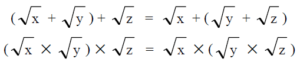
สมบัติการแจกแจง
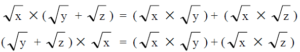
การบวกและการลบกรณฑ์ที่สอง
– กรณีที่ตัวเลขภายในกรณฑ์เท่ากัน ให้นำตัวเลขหน้ากรณฑ์มาบวก หรือลบกัน โดยตัวเลข ภายในกรณฑ์มีค่าเท่าเดิม เช่น
– กรณีที่ตัวเลขภายในกรณฑ์ไม่เท่ากัน ให้ทำให้ตัวเลขภายในกรณฑ์เท่ากันก่อน จึงนำตัวเลขหน้ากรณฑ์มาบวกหรือลบกัน เช่น
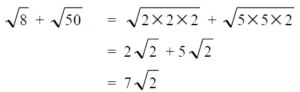
การคูณกรณฑ์ที่สอง
ให้นำตัวเลขหน้ากรณฑ์คูณกันและนำตัวเลขภายในกรณฑ์คูณกัน แล้วทำให้อยู่ในรูปอย่างง่าย เช่น
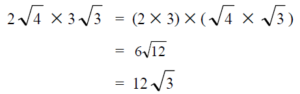
การหารกรณฑ์ที่สอง
ทำให้กรณฑ์อยู่ในรูปอย่างง่าย แล้วนำตัวเลขหน้ากรณฑ์มาหารกัน และ นำตัวเลขภายในกรณฑ์มาหารกัน เช่น
ทำให้กรณฑ์อยู่ในรูปอย่างง่าย แล้วนำตัวเลขหน้ากรณฑ์มาหารกัน และ นำตัวเลขภายในกรณฑ์มาหารกัน เช่น