การเขียน แผนภาพ เวนน์-ออยเลอร์-เซต คณิตศาสตร์ ม.4
แผนภาพ เวนน์-ออยเลอร์
แผนภาพเวนน์-ออยเลอร์
แผนภาพออยเลอร์(Eulerdiagram)เป็นแผนภาพที่ใช้ในการอธิบายความสัมพันธ์ของเซตต่างๆโดยให้วงกลมแต่ละวงแทนแต่ละเซตและแสดงความสัมพันธ์ของแต่ละเซตด้วยการครอบซึ่งแสดงความเป็นสับเซตการทับซ้อนกันหรือการไม่ทับซ้อนกันซึ่งแสดงว่าทั้งสองเซตไม่มีความสัมพันธ์กัน ลักษณะแผนภาพวงกลมเช่นนี้เชื่อว่าถูกใช้ครั้งแรกโดยนักคณิตศาสตร์ชาวสวิสนามว่าเลออนฮาร์ดออยเลอร์แผนภาพออยเลอร์นั้นมียังลักษณะคล้าย คลึงกันกับแผนภาพเวนน์มากในทฤษฎีเซตซึ่งเป็นแขนงหนึ่งของคณิตศาสตร์จึงนิยมใช้แผนภาพประยุกต์จากแผนภาพทั้งสองในการอธิบายเซตต่าง ๆ ให้เข้าใจได้ง่ายยิ่งขึ้น แผนภาพเวนน์–ออยเลอร์เป็นแผนภาพแสดงความเกี่ยวข้องของเซตต่าง ๆ ซึ่งชื่อที่ใช้เรียกเป็นชื่อของนักคณิตศาสตร์สองคน คือ จอห์น เวนน์ และ เลโอนาร์ด ออยเลอร์
การเขียนแผนภาพเวนน์–ออยเลอร์
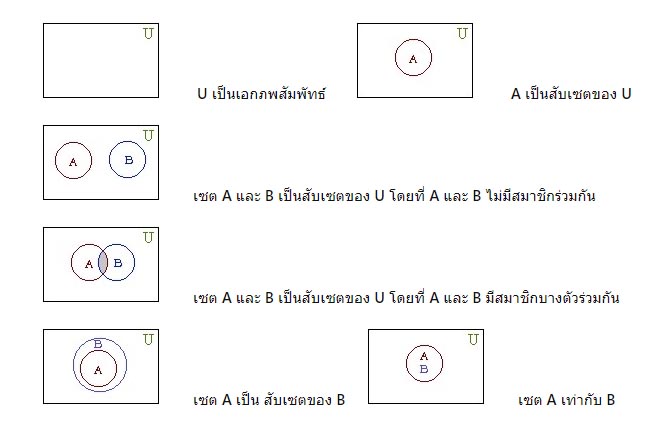
การเขียนแผนภาพเวนน์–ออยเลอร์มักเขียนแทนเอกภพสัมพัทธ์U ด้วยสี่เหลี่ยมผืนผ้าหรือรูปปิดใดๆ ส่วนเซต A,B,C,D,… ซึ่งเป็นเซตย่อยของ Uอาจเขียนแทนด้วยวงกลมหรือวงรีหรือรูปปิดใดๆโดยให้ภาพที่แทนเซตย่อยอยู่ในรูปสี่เหลี่ยมผืนผ้าที่แทนเอกภพสัมพัทธ์
การพิจารณาเกี่ยวกับเซตจะง่ายขึ้น ถ้าเราใช้แผนภาพของเวนน์-ออยเลอร์ เข้ามาช่วย หลักการเขียนแผนภาพมีดังนี้
1. ใช้รูปสี่เหลี่ยมผืนผ้าหรือสี่เหลี่ยมมุมฉากแทนเอกภพสัมพัทธ์
2. ใช้วงกลมหรือวงรีหรือรูปปิดใด ๆ แทนเซตต่าง ๆ ที่เป็นสมาชิกของ และเขียนภายในสี่เหลี่ยมผืนผ้า
ถ้ากำหนดให้ U = {1,2,3,4,5,6,7,8,9,10} A = {1,2,3} , B = {1,2,3,4,5} , C = {3,5,6,7}
เราจะเขียนแผนภาพเวนน์–ออยเลอร์ แสดงเอกภพสัมพัทธ์ U และเซตย่อยต่าง ๆ ดังแผนภาพต่อไปนี้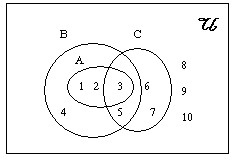
การใช้แผนภาพเวนน์–ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล
การใช้แผนภาพเวนน์-ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล เราจะวาดแผนภาพตามสมมติฐานที่เป็นไปได้ แล้วพิจารณาว่าแผนภาพแต่ละกรณีแสดงผลสรุปตามที่สรุปไว้หรือไม่ ถ้าทุกกรณีแสดงผลตามที่กหนด แสดงว่าสมเหตุสมผล ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปนั้นไม่สมเหตุสมผล โดยจะใช้การอ้างเหตุผลโดยตรรกบทของตรรกศาสตร์เข้ามาตรวจสอบ
ข้อความที่ใช้อ้างเหตุผลมีอยู่ 4 แบบหลักๆ คือ (1-4) และอีก 2 แบบเพิ่มเติม คือ (5-6) ดังนี้

ในการใช้แผนภาพเพื่อตรวจสอบความสมเหตุสมผล จะต้องวาดแผนภาพตามเหตุผลหรือสมมติฐานทุกกรณีที่เป็นไปได้ ถ้าทุกกรณีแสดงผลตามที่กำหนด จะได้ว่า ข้อสรุปนั้น สมเหตุสมผล แต่ถ้ามีบางกรณีที่ไม่สอดคล้องกับผลสรุปแล้ว ผลสรุปนั้นจะไม่สมเหตุสมผล
ตัวอย่างที่ 1 จงพิจารณาข้อความต่อไปนี้ว่าสมเหตุสมผลหรือไม่
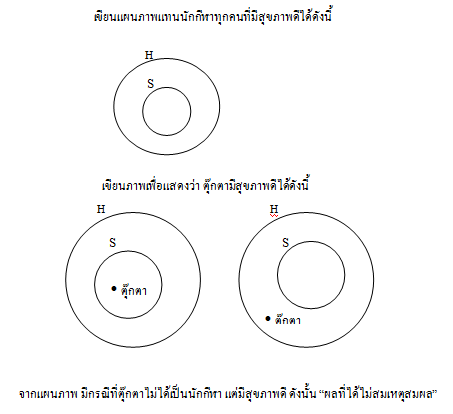
เหตุ นักกีฬาทุกคนมีสุขภาพดี
ตุ๊กตาสุขภาพดี
ผล ตุ๊กตาเป็นนักกีฬา
กำหนดให้ H แทนเซตของคนที่มีสุขภาพดี
S แทนเซตของนักกีฬา
ตัวอย่างที่ 2 จงพิจารณาข้อความต่อไปนี้ว่าสมเหตุสมผลหรือไม่
เหตุ เด็กไทยทุกคนเป็นคนดี
เจ้าจุกเป็นคนไทย
ผล เจ้าจุกเป็นคนดี
เขียนแผนภาพเวนน์-ออยเลอร์ได้ดังนี้
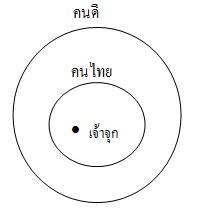
ดังนั้นข้อสรุปที่กล่าวว่าเจ้าจุกเป็นคนดี สมเหตุสมผล
ตัวอย่างที่ 3 จงพิจารณาข้อความต่อไปนี้ว่าสมเหตุสมผลหรือไม่
เหตุ นกทุกตัวเป็นสัตว์มีปีก
เป็ดทุกตัวเป็นสัตว์มีปีก
ผล นกทุกตัวเป็นเป็ดชนิดหนึ่ง
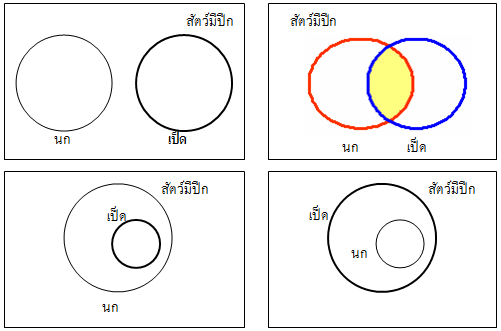
จาก 4 กรณีข้างต้น จะเห็นว่า นกและเป็ดต่างก้อเป็นสัตว์ปีก แต่เราสรุปไม่ได้แน่นอน นกเป็นเป็ดชนิดหนึ่ง
ดังนั้น ข้อนี้สรุปไม่สมเหตุสมผล…