ความรู้เบื้องต้นเกี่ยวกับสถิติ (Basic Statistics) – การแจกแจงความถี่
การแจกแจงความถี่
การแจกแจงความถี่เป็นวิธีการจัดเตรียมข้อมูลดิบให้เป็นหมวดหมู่เพื่อความสะดวกในการนำไปวิเคราะห์ ซึ่งสิ่งที่ควรคำนึงถึงในการแจกแจงความถี่ คือ
1) ถ้าข้อมูลดิบมีจำนวนน้อย ให้เรียงข้อมูลจากมากไปน้อย หรือเรียงลำดับจากน้อยไปหามาก ซึ่งข้อมูลที่เรียงลำดับแล้วเรียกว่า Ungrouped Data การวิเคราะห์ข้อมูลชนิดนี้จะได้ ค่าสูงสุด ค่าต่ำสุด และการกระจายของข้อมูล
2) ถ้าข้อมูลดิบมีจำนวนมาก (ข้อมูลตั้งแต่ 30 จำนวนขึ้นไป) ให้ทำการแจกแจงความถี่โดยตาราง ซึ่งเรียกว่า Grouped Data
2.1 การสร้างตารางการแจกแจงความถี่
การแจกแจงความถี่ทำได้ 2 ดังนี้
1) การแจกแจงความถี่ของลักษณะที่สนใจที่เป็นไปได้ทั้งหมด
2) การแจกแจงความถี่สำหลับค่าในแต่ละช่วงของลักษณะที่สนใจ
การแจกแจงความถี่ของลักษณะที่สนใจที่เป็นไปได้ทั้งหมด
การแจงแจกความถี่แบบนี้จะใช้กับข้อมูลที่จำนวนลักษณะที่เป็นไปได้ทั้งหมดมีไม่มากนัก เช่น จำแนกตามเพศ คือ เพศหญิง ชาย จำแนกตามความคิดเห็น เห็นด้วย ไม่เห็นด้วย ตัวอย่างที่ 2.1 จากการสำรวจคนไข้ที่เข้ามารับการรักษาที่โรงพยาบาลแห่งหนึ่งในเดือนมกราคม 2549 โดยแจกแจงความถี่ (จำนวนคนไข้)ตามเพศ ได้ดังนี้
|
เพศ |
จำนวนคนไข้ |
|
ชาย |
389 |
|
หญิง |
311 |
|
รวม |
700 |
การแจกแจงความถี่สำหรับค่าในแต่ละช่วงของลักษณะที่สนใจ
ในกรณีที่ค่าของข้อมูลที่เป็นไปได้ทั้งหมดของลักษณะที่สนใจมีจำนวนมากตัวอย่าง 2.2 ถ้าเลือกชายมา 100 คนสอบถามความสูงแล้วจัดทำเป็นช่วงๆได้5ช่วงหรือ 5 ช่วง ดังนี้
|
ความสูงของนักศึกษาชาย (เซนติเมตร) |
จำนวนคนไข้ |
|
135-144 |
5 |
|
145-154 |
21 |
|
155-164 |
39 |
|
165-174 |
24 |
|
175-184 |
11 |
|
รวม |
100 |
ช่วงจำนวนของแต่ละชั้น เช่น 135-144,145-154,…,175-184 เรียกว่าขีดจำกัดชั้น
ค่าต่ำสุดของแต่ละชั้น เช่น 135-145,…,175 เรียกว่าขีดจำกัดล่าง
และค่าสูงสุดของแต่ละชั้น เช่น 144,154,…,184 เรียกว่าขีดจำกัดบน
โดยทั่วไปจะกำหมดค่าสูงสุดและค่าต่ำสุดของแต่ละชั้นให้มีทศนิยมมากกว่าของข้อมูลดังนี้ตัวอย่าง 2.2. ถ้านักศึกษาชายคนหนึ่งสูง 144.5 เซนติเมตร ก็ไม่สามารถจัดให้นักศึกษาอยู่ในชั้นใดได้ นอกจากนั้นการกำหมดให้มีจำนวนหลังจุดทศนิยมมากกว่าค่าของของข้อมูลทำให้ข้อมูลทั้งหมดต่อเนื่องกัน และเรียกช่วงในแต่ละชั้นว่า ขอบเขตจำกัดดังนั้นจากตัวอย่างที่ 2.2 ขอบเขตจำกัดชั้นสามารถกำหมดได้ ดังนี้
|
ขอบเขตจำกัดชั้นสูงนักศึกษาชาย (เซนติเมตร) |
จำนวนคน |
|
134.5-144.5 |
5 |
|
144.5-154.5 |
21 |
|
154.5-164.5 |
39 |
|
164.5-174.5 |
24 |
|
174.5-184.5 |
11 |
|
รวม |
100 |
ค่าต่ำสุดของแต่ละชั้นคือ 134.5,144.5,…,174.5 เรียกว่าขอบเขตจำกัดล่างและค่าสูงสุดของแต่ชั้นคือ 144.5,154.5,….,1184.5 ว่าขอบเขยจำกัดบนและความกว้างของชั้นคือ 144.5-134.5=10
ตารางแจกแจงความถี่เป็นตารางที่อ่านเข้าง่าย แต่ก็มีการเสียรายละเอียดบางอย่างเกี่ยวข้อมูล เช่นมีนักศึกษาที่มีความสูงในช่วง 144.5- 154.5 เซนติเมตร อยู่ 18คน แต่จะไม่ทราบว่านักศึกษา 18 คน คนนี้มีส่วนสูงจริงๆ เท่าไหร่อาจจะเท่ากันหมดคือ 145 เซนติเมตรก็ได้ ปัญหานี้อาจแก้ไขด้ายโดยลดความกว้างของชั้นให้แคบลง ผูสร้างตารางแจกแจงความถี่จะต้องคำนึงถึงความเหมาสมในการกำหมดความกว้างของชั้นด้วย
2.2 ขั้นตอนการสร้างตารางแจกแจงความถี่
ขั้นตอนการสร้างตารางแจกแจงความถี่
การสร้างตารางแจกแจงความถี่มีขั้นตอน ดังนี้
1). หาค่าพิสัยของข้อมูลโดยที่ค่าพิสัย(Range)คือผลต่างระหว่างข้อมูลที่มีค่ามากที่สุดกับข้อมูลที่มีค่าน้อยที่สุดดังนั้น
|
พิสัย = ค่าสูงสุด – ค่าต่ำสุด |
ถ้ามีข้อมูล N ค่า คือ X1 ,X2,…XNและให้ Xmax = ค่าสูงสุดของข้อมูล = max(X1 ,X2,…XN)
Xmin = ค่าต่ำสุดของข้อมูล = min (X1 ,X2,…XN)
ดังนั้น พิสัย = R = Xmax – Xmin
2)กำหมดจำนวนชั้น (k)
โดยกำหนดจำนวนชั้นเป็น 5-20 ชั้น ถ้าข้อมูลมีการกระจายมากและมีจำนวนข้อมูลไม่มากควรให้มีจำนวนชั้นน้อยๆ เพื่อป้องกันไม่ให้มีชั้นที่มีชั้นที่มีค่าความถี่เป็นศูนย์ เนื่องจากไม่มีข้อมูลค่าใดที่ตกอยู่ในชั้นๆเลยในกรณีนี้ที่สร้างไม่ทราบว่าควรกำหมดให้ตารางแจกแจงความถี่มีกี่ชั้นส่ามารถใช้สูตรในการคำนวณชั้นได้ ด้งนี้
|
K = 1+ 3.3 log N |
3).คำนวณหาความกว้างของชั้นหรืออันตรภาคชั้น (Class Interval: I)
|
I = ความกว้างของชั้น (อันตรภาคชั้น) = พิสัย จำนวนชั้น =R/k |
ถ้าค่า I เป็นเลขไม่ลงตัว จะปัดให้เป็นจำนวนเต็ม(ไม่ว่าเศษจะมีค่าต่ำกว่าหรือมากกว่า 0.5)โดยทั่วไปมักกำหมดให้ความกว้างของแต่ละชั้นเท่ากันหมด แต่ละในทางปฏิบัติบางครั้งอาจจะให้ความกว้างของแต่ละชั้นไม่เท่ากัน หรืออาจกำหมดให้เป็นชั้นเปิดก็ได้หรืออาจจะกำหมดให้ความกว้างของชั้นเป็นค่าที่ทำให้ค่ากึ่งกลางชั้น มีค่าเท่ากับจริงของข้อมูล
|
ค่ากึ่งกลางชั้น = (ขอบเขตกำจัดบน + ขอบเขตจำกัดล่าง )/2 = (ขีดจำกัดบน + ขีดจำกัดล่าง )/2 |
4).คำนวณหาขีดจำกัดชั้น
โดยจะกำหมดให้ขีดจำกัดล่างของชั้นแรก (ชั้นที่มีค่าต่ำสุด) ครอบคลุมข้อมูลที่มีค่าต่ำสุดและให้ขีดจำกัดบนของชั้นสุดท้าย (ชั้นที่มีค่าสูงสุด)ครอบคลุมข้อมูลที่มีค่าสูงสุด หรืออาจใช้สูตรต่อไปนี้
|
ขีดจำกัดล่างของชั้นแรก = ค่าต่ำ – (Ik – R)/2 |
แล้วปัดให้มีลักษณะเหมือนข้อมูลจริง เช่น ข้อมูลมีจำนวนหลักหลังจุดทศนิยมสองหลักจะปิดเศษให้ขีดจำกัดชั้นเป็นเลขที่มีจำนวนจุดทศนิยมสอง 2 เช่นกัน
5).คำนวณหาขอบเขตจำกัดชั้น (Class Boundaries)
การหาขอบเขตชั้นนั้นจะกำหนดให้ขอบเขตชั้นมีจำนวนหลักหลังจุดทศนิยมมากกว่าของข้อมูลจริงอยู่ 1 หลักเสมอ เช่น ถ้าข้อมูลจริงเป็นเลขจำนวนเต็ม ขอบเขตจำกัดชั้นจะมีจำนวนจุดทศนิยม 1 หลัก ในทางปฏิบัติ เราสามารถหาค่าขอบเขตชั้นได้ ดังนี้
|
ขอบเขตจำกัดชั้น = (ขีดจำกัดบนของชั้น + ขีดจำกัดล่างของชั้นถัดไป)/2 |
6). นับจำนวนค่าของข้อมูล (ความถี่) ในแต่ละชั้น
หลังจากสร้างขอบเขตจำกัดชั้นแล้ว จึงตรวจสอบว่าข้อมูลค่าใดอยู่ในชั้นได้บ้าง แล้วนับจำนวนข้อมูลในแต่ละชั้นเรียกว่า ความถี่ของชั้น
2.3 ฮิสโตแกรม (Histogram)
ฮิสโตแกรม (Histogram)
กราฟแท่งแบบเฉพาะ โดยแกนตั้งจะเป็นตัวเลขแสดง “ ความถี่ ” และมีแกนนอนเป็นข้อมูลของคุณสมบัติของสิ่งที่เราสนใจ โดยเรียงลำดับจากน้อย ที่ใช้ดูความแปรปรวนของกระบวนการ โดยการสังเกตรูปร่างของฮิสโตแกรมที่สร้างขึ้นจากข้อมูลที่ได้มาโดยการสุ่มตัวอย่างมีประโยชน์ในการที่จะทำให้ทราบถึงการแจกแจงของสิ่งที่เราต้องการวิเคราะห์ ประโยชน์ประการสำคัญของการใช้ฮีสโตแกรม คือการใช้เพื่อวิเคราะห์ความถี่ของข้อมูลแล้วตัดสินใจว่า การแจกแจงหรือการกระจายข้อมูลแบบใด เพื่อใช้ตรวจสอบคุณสมบัติของข้อมูล ตลอดจนการประมาณการลักษณะคุณภาพที่ได้จากการผลิตแผนภูมิฮิสโตแกรม แผนภูมินี้จะชี้ให้เห็นถึงความเบี่ยงเบนของข้อมูลว่ามีลักษณะการกระจายตัวของข้อมูลเป็นแบบระฆังคว่ำ (Normal Distribution) หรือไม่ หรือมีความเบี่ยงเบนไปทางบวกหรือลบ หรือมีลักษณะรูปแบบแบบฟันเลื่อย หรือแบบหน้าผา เป็นต้น ทำให้มองเห็นว่าความเบี่ยงเบนที่เกิดขึ้นจาก Normal Distribution ควรจะแก้ไขอย่างไร
เมื่อไรจึงจะใช้แผนภาพฮิสโตแกรม
• เมื่อต้องการตรวจสอบความผิดปกติ โดยดูการกระจายของกระบวนการทำงาน
• เมื่อต้องการเปรียบเทียบข้อมูลกับเกณฑ์ที่กำหนด หรือค่าสูงสุด-ต่ำสุด
• เมื่อต้องการตรวจสอบสมรรถนะของกระบวนการทำงาน (Process Capability)
• เมื่อต้องการวิเคราะห์หาสาเหตุรากเหง้าของปัญหา (Root Cause)
• เมื่อต้องการติดตามการเปลี่ยนแปลงของกระบวนการในระยะยาว
• เมื่อข้อมูลมีจำนวนมากๆ
วิธีการเขียนฮิสโตแกรม (Histogram)
• เก็บรวบรวมข้อมูล (ควรรวบรวมประมาณ 100 ข้อมูล)
• หาค่าสูงสุด (L) และค่าต่ำสุด (S) ของข้อมูลทั้งหมด
• หาค่าพิสัยของข้อมูล (R-Range)
สูตร R = L – S
• หาค่าจำนวนชั้น (K)
สูตร K = Square root of (n) โดย n คือ จำนวนข้อมูลทั้งหมด
• หาค่าความกว้างช่วงชั้น (H-Class interval)
สูตร H = R/K หรือ พิสัย / จำนวนชั้น
• หาขอบเขตของชั้น (Boundary Value)
ขีดจำกัดล่างของชั้นแรก = S – หน่วยของการวัด / 2
ขีดจำกัดบนของชั้นแรก = ขีดจำกัดล่างชั้นแรก + H
• หาขีดจำกัดล่างและขีดจำกัดบนของชั้นถัดไป
• หาค่ากึ่งกลางของแต่ละชั้น (Median of class interval)
ค่ากึ่งกลางชั้นแรก = ผลรวมค่าขีดจำกัดชั้นแรก / 2
ค่ากึ่งกลางชั้นสอง = ผลรวมค่าขีดจำกัดชั้นสอง / 2
• บันทึกข้อมูลในรูปตารางแสดงความถี่
• สร้างกราฟฮิสโตแกรม
ลักษณะต่างๆ ของฮิสโตแกรม
• แบบปกติ (Normal Distribution)
การกระจายของการผลิตเป็นไปตามปกติ ค่าเฉลี่ยส่วนใหญ่จะอยู่ตรงกลาง
• แบบแยกเป็นเกาะ (Detached Island Type)
พบเมื่อกระบวนการผลิตขาดการปรับปรุง/หรือการผลิตไม่ได้ผล
• แบบระฆังคู่ (Double Hump Type)
พบเมื่อนำผลิตภัณฑ์ของเครื่องจักร 2 เครื่อง / 2 แบบมารวมกัน
• แบบฟันปลา (Serrated Type)
พบเมื่อเครื่องมือวัดมีคุณภาพต่ำ หรือการอ่านค่ามีความแตกต่างกันไป
• แบบหน้าผา (Cliff Type)
พบเมื่อมีการตรวจสอบแบบ Total Inspection เพื่อคัดของเสียออกไป
2.4. โพลิกอน
โพลีกอน (Polygon)
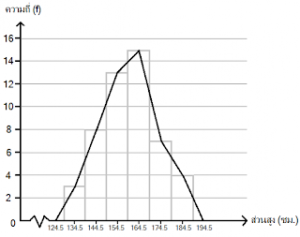
โพลีกอนหรือความถี่โพลีกอน (Frequency Polygon) เป็นการนำเสนอข้อมูลให้เห็นเด่นชัดยิ่งขึ้น ซึ่งแสดงผลโดยลากเส้นตรงเชื่อมต่อระหว่างค่ากึ่งกลางชั้นของฮีสโตแกรม แต่จะต้องเพิ่มในฮีสโตแกรมอีกสองชั้น คือ ชั้นต่ำสุด และชั้นสูงสุด โดยชั้นที่เพิ่มอีก 2 ชั้นมีค่าความถี่เป็นศูนย์
2.5 การแจกแจงความถี่สัมพัทธ์ (Relative Frequency Distribution)
การแจกแจงความถี่สัมพัทธ์ (Relative Frequency Distribution)
จากตารางแจกแจงความถี่ จะได้ความถี่สัมพัทธ์ของชั้นใดชั้นหนึ่งหมายถึงความถี่ของชั้นนั้นหารด้วยความถี่ทั้งหมด ส่วนมากนิยมเสนอด้วยเปอร์เซนต์โดยการนำผลหารขเางต้นคูณด้วย 100 และผลบวกของความถี่สัมพัทธ์ของทุกชั้นจะเท่ากับ 1
ความถี่สัมพัทธ์ที่ได้นิยมเขียนให้อยู่ในรูปทศนิยม หรือ ร้อยละ
ตัวอย่างที่ 8 จากตารางแจกแจงความถี่ที่กาหนดให้ หาค่าความถี่สัมพัทธ์ได้ดังนี้
|
อันตรภาคชั้น |
ความถี่ |
ความถี่สัมพัทธ์ |
ร้อยละความถี่สัมพัทธ์ |
|
10 – 14 |
3 |
3/30=0.1000 |
3/30×100=10.00 |
|
15 – 19 |
5 |
5/30=0.1667 |
5/30×100=16.67 |
|
20 – 24 |
12 |
12/30=0 4000 |
12/30×100= 40.00 |
|
25 – 29 |
10 |
10/30=0 3333 |
10/30×100=33.33 |
|
รวม |
30 |
1.0000 |
100 |
ความหมายจากตาราง
ความถี่สัมพัทธ์ของอันตรภาคชั้นใด เป็นการบอกให้ทราบว่าอันตรภาคชั้นนั้น มีจำนวนมากน้อยเพียงใด
เมื่อเทียบกับผลรวมของความถี่ทั้งหมด แต่เพื่อความเข้าใจได้ง่ายๆ จึงนิยมเขียนเป็นร้อยละ เรียกว่า “ร้อยละ
ของความถี่สัมพัทธ์”
เช่น อันตรภาคชั้น 10 – 14 มีร้อยละของความถี่สัมพัทธ์เท่ากับ 10.00 แสดงว่า อันตรภาคชั้น 10 –
14 มีจานวนคิดเป็นร้อยละ 10.00 ของจานวนข้อมูลทั้งหมด
อันตรภาคชั้น 20 – 24 เป็นอันตรภาคชั้นที่มีข้อมูลอยู่ในช่วงนี้มากที่สุด คิดเป็นร้อยละ 40.00 ส่วน
อันตรภาคชั้น 10 – 14 เป็นอันตรภาคชั้นที่มีข้อมูลอยู่ในช่วงนี้น้อยที่สุด คิดเป็นร้อยละ 10.00
หมายเหตุ
1. การปัดเศษในวิชาสถิติ แตกต่างกับการปัดเศษโดยทั่วๆไป กล่าวคือ ถ้าตัวที่จะปัดเป็น 5 โดยทั่วไปจะปัดขึ้น
แต่สำหรับวิชาสถิติ ต้องดูตัวเลขที่อยู่ข้างหน้า ถ้าเป็นเลขคู่ คือ 0, 2, 4, 6, 8 จะปัด 5 ทิ้ง แต่ถ้าตัวเลขที่อยู่
ข้างหน้าเป็นเลขคี่ คือ 1, 3, 5, 7, 9 จะปัดขึ้นเป็นหนึ่ง เช่น
12345/100,000=0.12345 ถ้าต้องการทศนิยม 4 ตาแหน่งจะได้ 0.1234
12375/100,000=0.12375 ถ้าต้องการทศนิยม 4 ตาแหน่งจะได้ 0.1238
2. ผลรวมของความถี่สัมพัทธ์ มีค่าเท่ากับ 1 เสมอ ส่วนผลรวมของร้อยละของความถี่สัมพัทธ์เท่ากับ 100 เสมอ
2.6 การแจกแจงความถี่สะสม
การแจกแจงความถี่สะสม
ความถี่สะสม (Cumulative Frequency) ของอันตรภาคชั้นใด คือ ผลรวมความถี่ตั้งแต่อันตรภาคชั้นช่วงคะแนนต่าสุดถึงอันตรภาคชั้นนั้น
ตัวอย่าง จากตารางแจกแจงความถี่ต่อไปนี้ จงหาความถี่สะสม
|
อันตรภาคชั้น |
ความถี่ |
ความถี่สะสม |
|
50 – 54 |
3 |
3 |
|
55 – 59 |
5 |
8 |
|
60 – 64 |
12 |
20 |
|
65 – 69 |
10 |
30 |
|
70 – 74 |
6 |
36 |
|
75 – 80 |
4 |
40 |
จากตารางแจกแจงความถี่ข้างต้น อันตรภาคชั้นที่ 3 มีความถี่สะสม 20 แสดงว่า
ข้อมูลที่มีค่าน้อยกว่า 64.5 มีอยู่ 20 จำนวนอันตรภาคชั้นที่ 4 มีความถี่สะสม 30 แสดงว่าข้อมูลที่มีค่าน้อยกว่า 69.5 มีอยู่ 30 จำนวนอันตรภาคชั้นที่ 5 มีความถี่สะสม 36 แสดงว่าข้อมูลที่มีค่าน้อยกว่า 74.5 มีอยู่ 36 จำนวนอันตรภาคชั้นที่ 6 มีความถี่สะสม 40 แสดงว่าข้อมูลที่มีค่าน้อยกว่า 80.5 มีอยู่ 40 จำนวน
ข้อสังเกต
1. ค่าความถี่สะสมหาได้จากการบอกความถี่จากอันตรภาคชั้นที่คะแนนมีค่าน้อยไปสู่ชั้นที่มีค่ามาก
2. ความถี่สะสมของอันตรภาคชั้นสุดท้าย คือ จานวนข้อมูลทั้งหมดนั่นเอง
3. ค่าความถี่สะสมของอันตรภาคชั้นใดบอกให้ทราบว่า มีจานวนข้อมูลเท่าใดที่มีค่าน้อยกว่าขอบบนของชั้นนั้น
4. ค่าความถี่ของอันตรภาคชั้นใด บอกให้ทราบว่า มีจานวนข้อมูลเท่าใดที่มีค่าอยู่ในอันตรภาคชั้นนั้น






