ความรู้เบื้องต้นเกี่ยวกับสถิติ-เปอร์เซ็นต์ไทล์ เดไซล์ ควอร์ไทล์

4.2 เดไซล์ (Decile Rank)

เดไซล์ (Decile Rank)

   เดไซล์ หมายถึงตำแหน่งที่แสดงให้ทราบว่ามีจำนวนข้อมูลเท่าไรใน 10 ส่วนของจำนวนข้อมูลทั้งหมดที่มีค่าต่ำกว่าข้อมูลที่ตำแหน่งนั้น เช่น นักเรียนคนหนึ่งสอบวิชาภาษาไทยได้คะแนน 55 คะแนนและคะแนน 55 นี้ อยู่ในตำแหน่งเดไซล์ที่ 7(D7) หมายความว่า 7 ใน 10 ของนักศึกษากลุ่มนั้นได้คะแนนวิชาภาษาไทยต่ำกว่า 55 คะแนน และ 3 ในการ 10 ของนักศึกษากลุ่มนั้นได้คะแนนวิชาภาษาไทยสูงกว่า 55 คะแนน

เปรียบเทียบเดไซล์ และเปอร์เซ็นต์ไทล์ ดังนี้

D 1    =  P 10

D 2    =  P 20

…      =  …

D 10   =  P 100

เปอร์เซนไทล์แบ่งข้อมูลออกเป็น 100 ส่วน แต่เดไซล์แบ่งเป็น 10 ส่วน ใช้ข้อมูลในตารางเดิมก็แล้วกัน จะหาเดไซล์ที่ 8 ได้จาก อันดับแรกก็หา

ตำแหน่งเดไซล์ก่อน คือ = (D x N) /10 = (8 x 280)/10 = 224 อยู่ในชั้น 61 – 70

ได้ D8 = 65.7 เพราะฉะนั้น เดไซล์ที่ 8 เท่ากับ 65.7 คะแนน

4.3 ควอร์ไทล์ (Quartile Rank)

ควอร์ไทล์ (Quartile Rank)

คุวอรํใทล์ หมายถึงตำแหน่งที่แสดงให้ทราบว่ามีจำนวนข้อมูลเท่าไรใน 4 ส่วนของจำนวนข้อมูลทั้งที่มีคำตากว่าข้อมูลที่ตำแหน่งนั้น เซ่น นักศึกษาคนหนึ่งสอบวิชาภาษาไทยได้ 72 คะแนนและคะแนน 72 นั้นอยู่ในตำแหน่งควอรไทลที่ 3 (Q s) หมายความว่า 3 ใน 4 ของศึกษากลุ่มนั้นได้คะแนนวิชาไม่ต่ำกว่า 72 คะแนน และ 1 ใน 4 ของนักศึกษากลุ่มนั้นได้คะแนนวิชาภาษาไทยสูงกว่า  72 คะแนน

เปรียบเทียบควอร์ไทล์ และเปอร์เซ็นตํไทล์ ดังนี้

Q l = P 25

Q 2 = P 50

Q 3 = P 75

Q 4 = P 100

ดังนั้น การคำนวณหาควอรไทล์จีงใช้วิธีเดียวกันกับการคำนวณหาเปอร์เซ็นต์ไทล์ ต่างกันที่การ แบ่งหมู่เท่านั้น คือ การคำนวณควอรไทล์ ต้องแบ่งหมู่ออกเป็น 4 ส่วน แต่เปอร์เซ็นต์ไทล์แบ่งหมู่ ออกเป็น 100 ส่วน

จงคำนวณหาคะแนนในตำแหน่ง Q 3 ซึ่งคะแนนของศึกษา 50 คน ดังนี้

วิธีทำ สร้างตารางแจกแจงความถี่สะสมคะแนนน้อยไปหาน้อยไปมากคะแนนมาก

Q 3 ของข้อมูลชุดนี้อยู่ในตำแหน่งที่ (Q*N)/4

=  (3*50)/4

=   37.5

ตำแหน่งที่ 37.5  อยู่ในชั้นมีคะแนนระหว่าง 50-59 ดังนั้น

F n  =  37.5

L    =  49.5

I     =  10

F 1  =  33

F2  =  41

จากสูตร  Q r  =  L+I{(F n-F 1)/(F 2-F 1)}

Q 3 =  49.5+10{(37.5-33)/(41-33)}

=  49.5+10{(4.5)/(8)}

=  49.5+5.625

=  55.125

ดังนั้น คะแนนที่ตำแหน่งชุดนี้ คือ 55.125

สรุป

ตำแหน่งของ ควอร์ไทล์  เดไซล์  และ  เปอร์เซ็นต์ไทล์
กรณีข้อมูลที่ไม่ได้แจกแจงความถี่
ถ้าข้อมูลมีจำนวนทั้งหมด N แล้ว

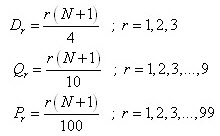
หมายเหตุ**  ถ้าข้อมูลมีจำนวน N น้อย ไม่นิยมหาค่า  เปอร์เซ็นต์ไทล์
กรณีข้อมูลที่แจกแจงความถี่
ถ้าข้อมูลมีจำนวนทั้งหมด N แล้ว
หลังจากที่หาตำแหน่งได้  ต่อไปก็เป็นการหาค่าของแต่ละอย่าง  ซึ่งทำได้ 2 วิธี คือ
1. โดยการคำนวณ
2. โดยการใช้กราฟ
การคำนวณ
กรณีที่ข้อมูลไม่แจกแจงความถี่ หลังจากที่ทราบตำแหน่ง และ เรียงข้อมูลแล้ว เราก็จะรู้ว่าค่าที่ต้องการอยู่ตำแหน่งอะไร  เช่น  ข้อมูลชุดหนึ่งมีดังนี้     2,6,18,25,32,64

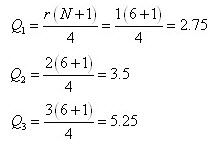
ตัวที่ 2.75 ซึ่งก็คืออยู่ระหว่างตัวที่ 2 และ 3 หรือค่า 6 กับ  18 นั่นเอง
ตัวที่ 3.5 ซึ่งก็คืออยู่ระหว่างตัวที่ 3 และ 4 หรือค่าที่ 18 กับ 25 นั่นเอง
ตัวที่ 5.25 ซึ่งก็คืออยู่ระหว่างตัวที่ 5 และ 6 หรือค่า 32 กับ 64 นั่นเอง
จากนั้นให้ทำการเทียบ  ว่าตำแหน่งห่างกันเท่าไร  แล้วค่าจะห่างกันเท่าไร  เช่น  ถ้าต้องการหา  Q₁ จะได้ว่า      จากข้อมูลจริง  ตัวที่ 2 และ 3 ซึ่งห่างกัน 1 ตำแหน่ง แล้วค่าของข้อมูลตางกัน 18 – 6 =12 แต่ต้องการตัวที่ 2.75 ดังนี้ ตัวที่ 2 และ 2.75 ซึ่งห่างกัน 0.75 ตำแหน่ง แล้วค่าของข้อมูลต่างกัน

ดังนั้น ตัวที่ 2.75 มีค่าเท่ากับ  6 + 9 = 15  (เทียบจากตัวที่ 2 นั่นเอง) หรือ  Q₁= 15
กรณีที่ข้อมูลแจกแจงความถี่แล้ว แต่ยังไม่เขียนเป็นอันตรภาคชั้น  ยังคงเทียบเหมือนแบบแรก
กรณีที่ข้อมูลแจกแจงความถี่และเขียนเป็นอันตรภาคชั้น
– ค่าขอบบนของอันตรภาคชั้นนั้นจะ   คือร้อยละของความถี่สะสมสัมพัทธ์ของ อันตรภาคชั้นนั้น
เช่น   ถ้า     อันตรภาค                   ร้อยละของความถี่สะสมสัมพัทธ์
65 – 69                                     35
70 – 74                                     56
จะได้ว่า P35 = 69.5 และ P56 = 74.5 เป็นต้น
– ใช้สูตร

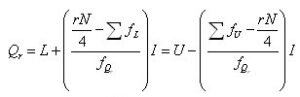
โดยที่ L คือ  ขอบล่างของชั้นที่ Q_r  ตกอยู่

คือ  ผลรวมของความถี่ของชั้นที่ต่ำกว่าชั้นที่ Q_r อยู่
คือ  ผลรวมของความถี่ของชั้นที่ต่ำกว่าชั้นที่ Q_r อยู่ + ความถี่ของชั้นที่ Q_r อยู่
คือ  ความถี่ของชั้นที่ Q_r อยู่
I   คือ  ความกว้างของอันตรภาคชั้น ซึ่งต้องเท่ากันทุกชั้น
กรณีสูตรอื่นๆ ก็เหมือนกัน เพียงแต่เปลี่ยนตำแหน่งจาก   เป็นอื่นๆ ตามแบบของมัน
โดยการใช้กราฟ
1. เขียนโค้งความถี่สะสมหรือโอจีฟ
2. หาตำแหน่งของควอไทล์ เดไซล์ หรือ เปอร์เซ็นต์ไทล์ที่ต้องการหา
3. ลากจากแกนตั้ง ซึ่งเป็นแกนของความถี่สะสม ซึ่งตรงกับตำแหน่งที่ต้องการทราบมาตัดกับโค้งโอจีฟ แล้วโปรเจ็คลงมาบนแกนนอน ซึ่งเป็นแกนของข้อมูล ก็จะทราบค่านั้น
หมายเหตุ**   กรณีที่ข้อมูลเป็นอันตรภาคชั้นค่าในแต่ชั้นจะถูกครอบคลุมด้วยค่าของขอบบนกับขอบล่าง  เช่น  20 – 29, 30 – 39  หมายความว่า ค่าจริงๆอยู่ระหว่าง 19.5 และ29.5 – 39.5  เป็นต้น