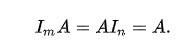เมทริกซ์เอกลักษณ์
เมทริกซ์เอกลักษณ์สำหรับการคูณ คือ เมทริกซ์จัตุรัสที่มีสมาชิกในแนวเส้นทแยงมุมหลักเท่ากับ 1 โดยตลอด ส่วนสมาชิกตัวอื่นมีค่าเป็นศูนย์หมด
ในพีชคณิตเชิงเส้นที่เมทริกซ์เอกลักษณ์ขนาดnเป็นn × n ตารางเมทริกซ์กับคนที่อยู่บนเส้นทแยงมุมหลักและศูนย์อื่น ๆ แสดงโดยI nหรือIถ้าขนาดไม่เป็นสาระสำคัญหรือสามารถกำหนดได้เล็กน้อยโดยบริบท
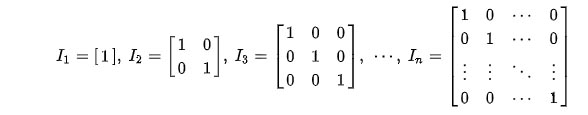
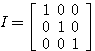
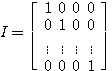
เห็นไหมครับนี้คือเมทริกซ์เอกลักษณ์ คงไม่ต้องอธิบายเป็นคำพูดนะว่ามันหมายถึงอะไรดูเอาแล้วกันว่าสมาชิกของมันเป็นอย่างไร 1 จะตั้งอยู่ตรงไหนและ 0 จะตั้งอยู่ตรงไหน นี่แหละครับเขาเรียกว่าเมทริกซ์เอกลักษณ์สมาชิกในแนวเฉียงเป็นเลข 1 เสมอนอกนั้นเป็นเลข 0 เลยครับ
คำว่าเมทริกซ์หน่วยยังถูกนำมาใช้อย่างแพร่หลายเช่นกัน แต่เมทริกซ์เอกลักษณ์ในปัจจุบันเป็นมาตรฐานคำหน่วยเมทริกซ์ไม่ชัดเจนเพราะมันยังถูกใช้สำหรับเมทริกซ์ของคนและสำหรับการใด ๆหน่วยของแหวนทุกn × nเมทริกซ์
ในบางสาขาเช่นทฤษฎีกลุ่มหรือกลศาสตร์ควอนตัมเมทริกซ์เอกลักษณ์บางครั้งแสดงด้วยตัวหนา 1, 1หรือเรียกว่า “id” (ย่อมาจาก identity); มิฉะนั้นจะเป็นเหมือนผม ไม่บ่อยนักหนังสือคณิตศาสตร์บางเล่มใช้UหรือEเพื่อแสดงถึงเมทริกซ์เอกลักษณ์ซึ่งหมายถึง “เมทริกซ์หน่วย” และคำภาษาเยอรมันEinheitsmatrixตามลำดับ
เมื่อAคือm × nเป็นสมบัติของการคูณเมทริกซ์ที่
โดยเฉพาะอย่างยิ่งเมทริกซ์เอกลักษณ์ทำหน้าที่เป็นข้อมูลประจำตัวแบบทวีคูณของวงแหวนของเมทริกซ์n × nทั้งหมดและเป็นองค์ประกอบเอกลักษณ์ของกลุ่มเชิงเส้นทั่วไป GL ( n ) (กลุ่มที่ประกอบด้วยเมทริกซ์n × n แบบผกผัน ทั้งหมด) โดยเฉพาะอย่างยิ่งเมทริกซ์เอกลักษณ์เป็นตัวผกผันกับมันผกผันเป็นตัวเองได้อย่างแม่นยำ
ที่ไหนn × nเมทริกซ์ที่ใช้แทนการแปลงเชิงเส้นจากnปริภูมิเวกเตอร์มิติเพื่อตัวเองฉันnหมายถึงฟังก์ชั่นตัวตนโดยไม่คำนึงถึงพื้นฐาน
