สรุปสูตรสถิติ ม.6 ท่องก่อนเรียนและก่อนสอบ

สรุปสูตร สถิติ ทั้งหมด

1) ค่าเฉลี่ยเลขคณิต

2) มัธยฐาน

3) ฐานนิยม

4) ควอไทล์ เดไซล์ เปอร์เซนไทล์

และต่อ สรุปสูตรสถิติ ม.6 ท่องก่อนเรียนออนไลน์ ตอนที่ 2 เรื่อง

5) การวัดการกระจาย

6) ความแปรปรวน และความแปรปรวนรวม

7) ค่ามาตรฐาน พื้นที่ใต้เส้นโค้งปกติ

9) ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล

ค่าเฉลี่ยเลขคณิต

ค่าเฉลี่ย (Mean) คือค่ากลางของตัวเลขที่ใช้ในทางสถิติเพื่อบ่งบอกว่าข้อมูลส่วนมากนั้นใกล้เคียงค่านี้ ในบทความนี้ คุณจะได้เรียนรู้เกี่ยวกับค่าเฉลี่ียและวิธีการคำนวณหาค่าเฉลี่ยเลขคณิตอย่างง่าย พร้อมตัวอย่างการคำนวณทีละขั้นตอน มาเริ่มกันเลย

ค่าเฉลี่ยสามารถคำนวณได้จากการหาผลรวมของตัวเลข แล้วนำมาหารด้วยจำนวนของตัวเลขทั้งหมด ซึ่งสามารถนำมาเขียนเป็นสูตรได้คือ

ค่าเฉลี่ย = ผลรวมของตัวเลขทั้งหมด / จำนวนของตัวเลข

นี่เป็นสูตรอย่างง่ายเพียงสูตรเดียวสำหรับการหาค่าเฉลี่ย ต่อไปมาดูตัวอย่างกัน

ตัวอย่างที่ 1 จงหาค่าเฉลี่ยของตัวเลขต่อไปนี้

5, 8, 11

หาผลรวมของตัวเลขทั้งหมดจะได้ 5 + 8 + 11 = 24
นับจำนวนของตัวเลขทั้งหมดจะได้ 3 ตัวเลข
คำนวณหาค่าเฉลี่ยโดยแทนค่าลงในสูตรจะได้ 24 / 3 = 8

มัธยฐาน (Median)

มัธยฐาน คือ ค่าที่มีตำแหน่งอยู่กึ่งกลางของข้อมูลทั้งหมด เมื่อเรียบเรียงข้อมูลจากต่าน้อยที่สุดไปหาค่าที่มากที่สุด หรือจากค่าที่มากที่สุดไปหาค่าที่น้อยที่สุด เราอาจใช้ตัวย่อ “Med” แทนค่ามัธยฐานของข้อมูล

ค่ามัธยฐานอาจเป็ฯค่าใดค่าหนึ่งของข้อมูล หรืออาจเป็ฯค่าที่คำนวณขึ้นมาใหม่ ซึ่งไม่ตรงกับค่าของข้อมูลใดๆก็ได้ ค่ามัธยฐานนิยมใช้กับข้อมูล ซึ่งสูงกว่าหรือต่ำกว่าค่าอื่นมากๆ

1. การหาค่ามัธยฐานของข้อมูลที่ไม่แจกความถี่

เมื่อจัดเรียงข้อมูลชุดหนึ่งซึ่งมี N ค่า ตำแหน่งของมัธยฐาน จะคำนวณได้จากสูตร

ตัวอย่างที่ 1 จงหามัธยฐานของข้อมูลดังนี้ 5, 8, 3, 20, 100, 6

วิธีคิด เรียงข้อมูลจากน้อยไปมากได้ดังนี้ 3 5 6 8 20 100

ตำแหน่งของค่ามัธยฐาน คือ = (6+1)/2 = 3.5
ดังนั้น ค่ามัธยฐาน คือ = (6+8)/2 = 7 Ans

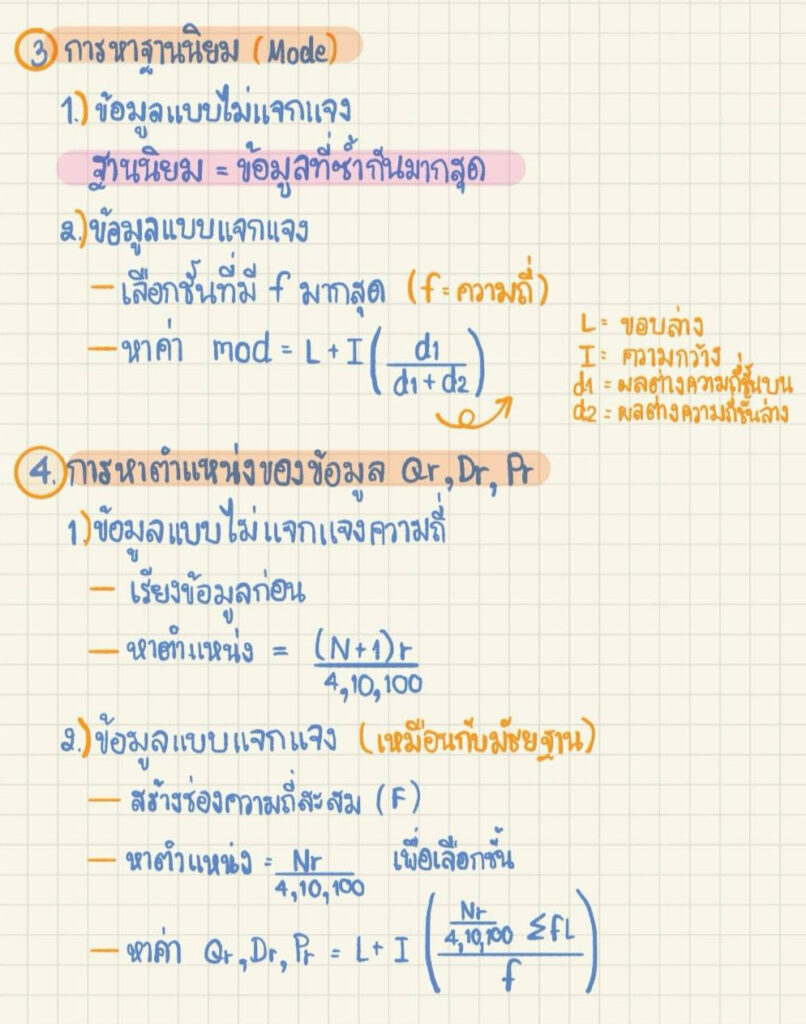
ฐานนิยม (Mode)

ฐานนิยม คือ ค่ากลางที่มีจำนวนมากที่สุด

หลักการในการหาฐานนิยม คือ หาตัวที่ซ้ำกันมากที่สุด และมีเงื่อนไขว่าในข้อมูลแต่ละชุดจะมีฐานนิยมได้อย่างมาก 22 ตัวเท่านั้น ถ้ามีมากกว่านั้นให้ถือว่าไม่มีฐานนิยม

ฐานนิยมของข้อมูลแบบไม่แจกแจงความถี่

ให้มองหาข้อมูลที่มีการซ้ำกันมากที่สุด เช่น ข้อมูลไม่แจกแจงความถี่ คือ 2,3,4,5,6,4,7,6,62,3,4,5,6,4,7,6,6 จะเห็นว่าในข้อมูลชุดนี้มี 66 อยู่ 33 ตัว ซึ่งเป็นจำนวนตัวที่มากที่สุดแล้วเมื่อเทียบกับตัวเลขอื่น ๆ ดังนั้น ฐานนิยมของข้อมูลชุดนี้คือ 66

ตัวอย่างการหาฐานนิยม

ข้อมูลชุดที่ 11 คือ 3,5,6,6,6,7,10,23,5,6,6,6,7,10,2 จะได้ว่าฐานนิยมคือ 66

ข้อมูลชุดที่ 22 คือ 2,5,5,8,9,10,11,82,5,5,8,9,10,11,8 จะได้ว่าฐานนิยมของข้อมูลชุดนี้มี 22 ค่า คือ 5 และ 85 และ 8 เนื่องจากข้อมูลทั้งสองค่ามีจำนวน 22ตัวเท่ากันและข้อมูลค่าอื่น ๆ มีเพียงตัวเดียว

ข้อมูลชุดที่ 33 คือ 1,1,1,2,3,3,3,5,6,6,6,71,1,1,2,3,3,3,5,6,6,6,7 จะได้ว่าข้อมูลชุดนี้จำนวนตัวที่ซ้ำมากที่สุดคือ 33 ตัว ซึ่งมีข้อมูลถึงสามค่าในชุดนี้ที่ซ้ำกัน 33 ตัว นั้นคือ 1,31,3 และ 66 ดังนั้นข้อมูลชุดนี้ถือว่าไม่มีฐานนิยม

ฐานนิยมของข้อมูลแจกแจงความถี่

ในตารางแจกแจงความถี่ การหาฐานนิยมยังใช้หลักการเดิม คือ การหาตัวที่ซ้ำมากที่สุด เช่น

คะแนน	จำนวน นักเรียน
20−3920−39	22
40−4940−49	55
50−6950−69	88
70−8970−89	55

จากตารางข้างต้น ถ้าเรามองผ่าน ๆ จะบอกว่าคะแนนที่น่าจะซ้ำมากที่สุดน่าจะอยู่ในชั้นที่ 33 เนื่องจากมีคนอยู่ในชั้นนี้มากที่สุด

แต่จริง ๆ แล้วเวลาเราจะดูว่าคนในห้องไหนแน่นที่สุดนั้น เราจะต้องเทียบคนที่อยู่ในห้องกับขนาดห้อง ไม่ใช้เพียงแค่จำนวนคนอย่างเดียว ดังนั้นเวลาจะตัดสินใจว่าฐานนิยมควรอยู่ในชั้นไหนจะต้องดูว่า จำนวนคนในชั้นนั้นหารด้วยความกว้างของชั้นนั้นต้องมากที่สุด

คะแนน	จำนวน นักเรียน	fIfI
20−3920−39	22	220=0.1220=0.1
40−4940−49	55	510=0.5510=0.5
50−6950−69	88	820=0.4820=0.4
70−8970−89	55	520=0.25520=0.25

จากตารางจะเห็นว่า ชั้นที่หนาแน่นที่สุดคือ ชั้นที่ 22 เราจึงคาดว่าฐานนิยมจะต้องอยู่ในชั้นนี้

โดยปกติข้อสอบจะออกประ้เภทที่ความกว้างชั้นเท่ากันเป็นหลัก เราไม่จำเป็นต้องดู fIfI ดูแค่ว่าชั้นไหนความถี่สูงสุดก็พอแล้ว

หลังจากนั้นเราจะวาดแผนภาพของระยะห่างทั้งหมดของฐานนิยม นั้นคือ การหาผลต่างของจำนวนนักเรียนในชั้นนั้นกับชั้นก่อนหน้า (dL)(dL) และ ผลต่างของจำนวนนักเรียนในชั้้นนั้นกับชั้นถัดไป (dU)(dU)

จากรูปด้านบนจะสรุปได้ว่า

ฐานนิยมของข้อมูลแจกแจงความถี่ คือ

ขอบล่างของชั้นที่มีฐานนิยม+I⋅(dLdL+dU)ขอบล่างของชั้นที่มีฐานนิยม+I⋅(dLdL+dU)

ชั้นที่มีฐานนิยมอยู่ คือ ชั้นที่ fiIfiI มีค่ามากที่สุด

การหาฐานนิยมของข้อมูลแจกแจงความถี่

จงหาฐานนิยมของข้อมูลแจกแจงความถี่ต่อไปนี้

คะแนน	จำนวน นักเรียน
40−4940−49	22
50−5950−59	55
60−6960−69	1717
70−7970−79	99
80−8980−89	88

จากตารางแจกแจงความถี่ที่กำหนดให้ สังเกตุว่า ความกว้างทุกชั้นเท่ากัน เราจึงสามารถบอกได้เลยว่า ฐานนิยมอยู่ในชั้นที่ความถี่สูงสุด นั้นก็คือ ชั้นที่ 33

ขอบล่างของชั้นที่ 33 คือ 59.559.5
ความกว้างชั้น คือ I=10I=10
ผลต่างของจำนวนคนชั้นนั้นกับชั้นก่อนหน้า คือ dL=17−5=12dL=17−5=12
ผลต่างของจำนวนคนชั้นนั้นกับชั้นถัดไป คือ dU=17−9=8dU=17−9=8

ดังนั้น

ฐานนิยม=59.5+10(128+12)=59.5+6=65.5ฐานนิยม=59.5+10(128+12)=59.5+6=65.5

ฐานนิยมของข้อมูลชุดนี้คือ 65.565.5

การหาค่าควอไทล์ เดไซล์ และเปอร์เซ็นต์ไทล์

ตัวอย่าง เด็กกลุ่มหนึ่งจานวน 7 คน มีอายุดังนี้ 14, 13, 19, 12, 17, 14 และ 16 ปี จงหา Q₁,Q₃ ,D₅

วิธีทำ ดำเนินตามขั้นตอนดังนี้

ขั้นที่ 1 เรียงลาดับข้อมูลจากน้อยไปหามากได้ดังนี้

12 13 14 14 16 17 19

ขั้นที่ 2 หาตำแหน่งที่ต้องการ

ขั้นที่ 3 คำนวณค่าในตำแหน่งที่ต้องการ

ค่าที่อยู่ในตำแหน่งที่ 2 ตรงกับ 13 พอดี ดังนั้น Q₁ =13 ปี

ค่าที่อยู่ในตำแหน่งที่ 6 ตรงกับ 17 พอดี ดังนั้น Q₃ =17 ปี

ค่าที่อยู่ในตำแหน่งที่ 4 ตรงกับ 14 พอดี ดังนั้น D₅ =14 ปี

ตัวอย่าง ผลการชั่งการน้ำหนัก (หน่วยเป็นกิโลกรัม) ของนักเรียนชั้น ม. 5 ห้องหนึ่งจานวน 31 คน เป็นดังนี้

42 53 68 49 68 56 44 38 60 51 48 45 44

58 62 45 50 66 54 62 43 57 65 70 52 57

69 65 64 48 62

1. จงหาว่าน้ำหนักจะต้องตรงกับกี่กิโลกรัมจึงจะทำให้นักเรียนประมาณสามในสี่ของห้องมีน้ำหนักมากกว่า

2. จงหาว่าน้ำหนักจะต้องตรงกับกี่กิโลกรัมจึงจะทำให้นักเรียนประมาณหกในสิบของห้องมีน้ำหนักมากกว่า

วิธีทำ เรียงข้อมูลจากน้อยไปหามากก่อน ดังนี้

38 42 43 44 44 45 45 48 48 49 50 51 52 53

54 56 57 57 58 60 62 62 62 64 65 65 66 68

68 69 70

1. น้ำหนักที่มีนักเรียนประมาณสามในสี่ของห้องที่มีน้ำหนักมากกว่า แสดงว่าต้องการหาน้ำหนักที่มีนักเรียน

ประมาณหนึ่งในสี่ของห้องที่มีน้าหนักน้อยกว่า นั่นคือ ต้องการหาน้าหนักที่ตรงกับ P₂₅ นั่นเอง

2. น้ำหนักที่มีนักเรียนประมาณหกในสิบของห้องที่มีน้ำหนักน้อยกว่า มีความหมายเช่นเดียวกับ

น้ำหนักที่มีนักเรียนประมาณ 60 ใน 100 ของห้องที่มีน้ำหนักน้อยกว่า ซึ่งตรงกับน้ำหนักที่ P₆₀

น้ำหนักในลำดับที่ 19 และ 20 คือ 58 และ 60 ตามลำดับ

ตำแหน่งต่างกัน 20 – 19 = 1 น้ำหนักต่างกัน 60 – 58 = 2 กิโลกรัม

ตำแหน่งต่างกัน 19.2 – 19 = 0.2 น้ำหนักต่างกัน 2×0.2=0.4 กิโลกรัม

ดังนั้น P₆₀ = 58 +0.4 = 58.4 กิโลกรัม

-ขอบคุณสูตรสรุปจาก https://www.facebook.com/thematrixmath/

และ เครดิต : Arisara Panlam

สรุปสูตรสถิติ ม.6 ตอนที่ 1 ท่องก่อนเรียนออนไลน์