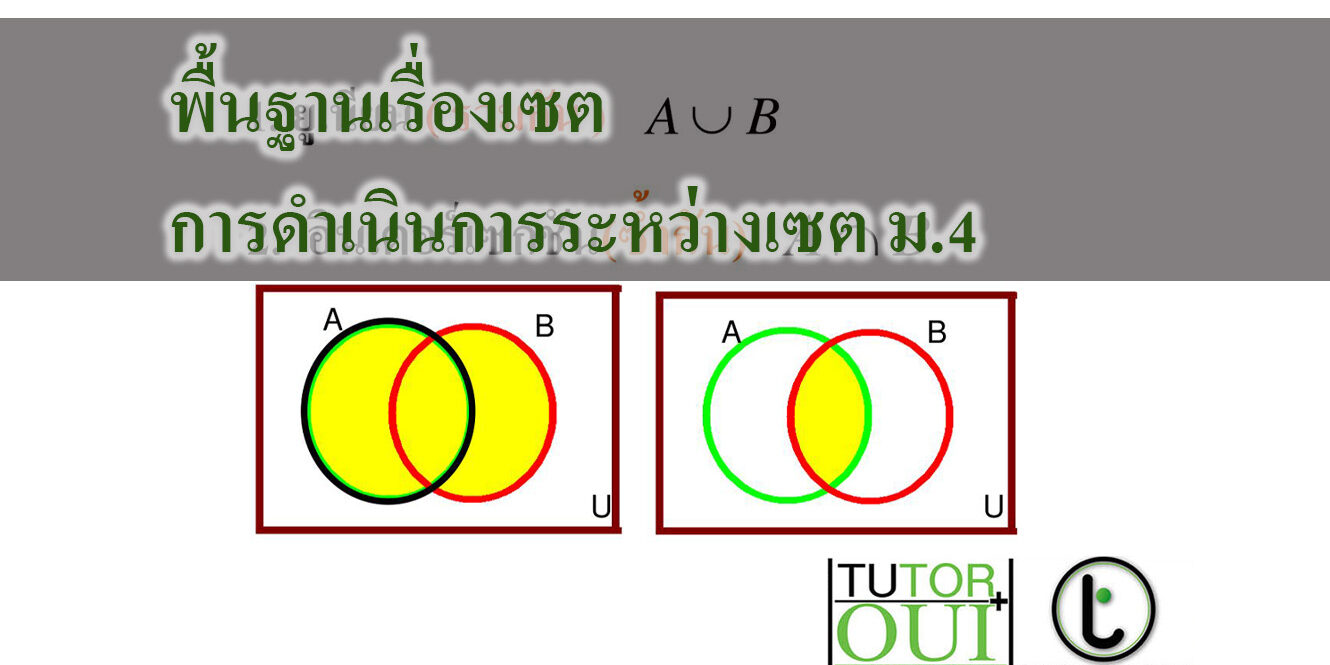
พื้นฐานเรื่องเซต-การดำเนินการระหว่างเซต คณิตศาสตร์ ม.4

การดำเนินการของเซต(Operation With set) เป็นการสร้างเซตขึ้นมาใหม่จากการนำเซตที่กำหนดให้ มาดำเนินการตามต้องการ ซึ่งจะมีการดำเนินการหลายแบบ เช่น ยูเนียนของเซต อินเตอร์เซกชันของเซต คอมพลีเมนต์ของเซต และผลต่าง

ยูเนียน (Union)

– ยูเนียน (Union) : ยูเนียนของเซต A และเซต B จะได้เซตใหม่ ซึ่งมีสมาชิกของเซต A หรือเซต B หรือทั้งสองเซต

“ ยูเนียนของเซตA และเซต B เขียนแทนด้วย A B ”

A B = {x| x A หรือ x เ ป็นสมาชิกของทั้งสองเซต}

เช่น A = {1,3,5} และ B = {3,6,9}

จะได้ A B ={1,3,5,6,9}

ดังนั้น ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B

ตัวอย่างเช่น A ={1,2,3}

B = {3,4,5}

∴ A U B = {1,2,3,4,5}

อินเตอร์เซกชัน

– อินเตอร์เซกชัน (Intersection): อินเตอร์เซกชันของเซต A และเซต B จะได้เซตใหม่ ซึ่งสมาชิกเป็นสมาชิกของเซตทั้งเซต A และเซต B

“ อินเตอร์เซกชันของเซตA และเซต B เขียนแทนด้วย A B ”

A B = {x| x A และ x B}

เช่น A = {1,2,3,4,} , B = {2,4,6} และ C = {0,1}

จะได้ A B = {2,4}

A C = {1}

B C = {}

ดังนั้น อินเตอร์เซกชัน (Intersection) มีนิยามคือเซต A อินเตอร์เซกชันเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B

ตัวอย่างเช่น A ={1,2,3}

B = {3,4,5}

∴ A ∩ B = {3}

คอมพลีเมนต์

– คอมพลีเมนต์ (Complement) : คอมพลีเมนต์ของเซต A คือ เซต A ที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่ใช่สมาชิกของเซต A

“คอมพลีเมนต์ของเซต A เขียนแทนด้วย A ”

A = {x| x € U และ x € A }

เช่น U ={0,1,2,3} , A ={0,2,4} และ B = {1,3}

จะได้ A = {1,3}

B = {0,2}

คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ แล้ว คอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’

ตัวอย่างเช่น U = {1,2,3,4,5}

A ={1,2,3}

∴ A’ = {4,5}

– ผลต่างระหว่างเซต (Difference of Sets ) : ผลต่างระหว่างเซต A และเซต B คือสมาชิกอยู่ในเซต B

“ผลต่างระหว่างเซต A และเซต B เขียนแทนด้วย A – B ”

A-B ={x| x € A และ x € B}

เช่น A = {0,1,2,3,4} และ B = {1,3,5,7,9}

จะได้ A-B = {0,2,4}

B-A = {5,7,9}

ผลต่าง(Differnce) บทนิยาม ถ้า A และ B ต่างก็เป็นสับเซตของเซต U ผลต่างของเซต A และ B คือ เซตที่ประกอบด้วยสมาชิกของเซต A แต่ไม่เป็นสมาชิกของ B เขียนแทนด้วย A – B

ตัวอย่าง กำหนดเซต A และ B จงหา A – B

กำหนด A = {3, 9}

B = {4, 6, 7}

A – B = {3, 9}