สรุปเข้มเรื่องจำนวนจริง บทพื้นฐานของคณิตศาสตร์ ม.ปลาย
โครงสร้างของระบบจำนวนจริง
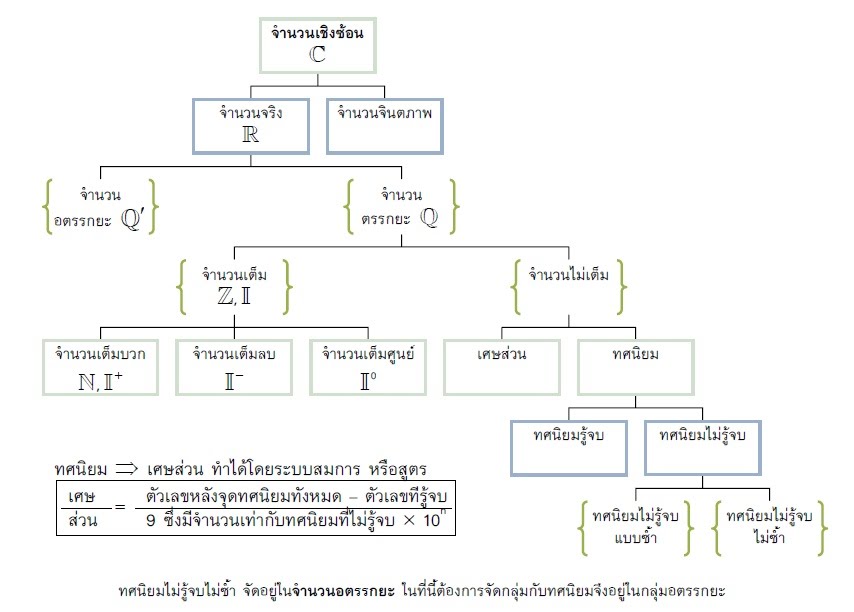
ก่อนอื่นมาดูโครงสร้างของจำนวนจริงกันก่อน จำนวนจริงประกอบไปด้วยจำนวนตรรกยะ และจำนวนอตรรกยะ
- จำนวนตรรกยะ คือ จำนวนที่เขียนเป็นเศษส่วนของจำนวนเต็มได้, ทศนิยมซ้ำ, รากที่ถอดได้ลงตัว
- จำนวนอตรรกยะ คือ จำนวนที่เขียนเป็นเศษส่วนของจำนวนเต็มไม่ได้, ทศนิยมที่ไม่ซ้ำ, รากที่ถอดได้ไม่ลงตัว, ค่าพิเศษ เช่น π,e
-
แผนภาพอีกเช่นเคย จะเห็นได้ว่า จำนวนตรรกยะ จะประกอบด้วยสองส่วนคือ จำนวนเต็ม และ จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม
- จำนวนเต็ม คือจำนวนที่เป็นตัวเลขเต็มๆ หรือ ตัวเลขที่ไม่มีทศนิยมนั่นเอง นั่นคือ ตัวเลขที่เราใช้นับนั่นเอง ยกตัวอย่างเช่น 1, 2, 3, 4 … ทั้งนี้ทั้งนั้น รวมไปจนถึงค่าที่ติบลบของจำนวนนับนี้และศูนย์ด้วย เช่น 0, -1, -2, -3, -4 ….
- จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม ความหมายของจำนวนนี้ก็ตามความหมายของชื่อเลยครับ นั่นคือ ตัวเลขเขียนในรูปของทศนิยมซ้ำได้โดยที่ไม่ได้เป็นเลขจำนวนเต็มนั่นเอง อย่างเช่น 1/2=0.5 หรือ 1/3 = 0.333… (สามซ้ำ)
ยิ่งไปกว่านั้น จำนวนเต็มยังแบ่งย่อยได้อีกสามหมวดคือ จำนวนเต็มลบ จำนวนเต็มบวก และ จำนวนเต็มศูนย์

สมบัติของจำนวนจริง
ถ้าให้ a, b และ c เป็นจำนวนจริงใดๆ แล้ว จะได้ว่าจำนวนจริงจะมีสมบัติดังต่อไปนี้
1. สมบัติปิดการบวก: a+ b จะต้องเป็นจำนวนจริงเสมอ
2. สมบัติการเปลี่ยนหมู่ของการบวก: a + (b + c) = (a + b) + c
3. สมบัติการมีเอกลักษณ์การบวก: a + 0 = a = 0 + a โดยที่เราเรียก 0 ว่าเอกลักษณ์ของการบวก
4. สมบัติการมีอินเวอร์สของการบวก: a + (-a) = 0 = (-a) + a โดยที่ (-a) เป็นอินเวอร์สการบวกของ a
5. สมบัติปิดของการคูณ: a คูณ b หรือ ab จะต้องมีผลลัพธ์เป็นจำนวนจริงเสมอ
6. สมบัติการเปลี่ยนหมู่ของการคูณ: a(bc) = (ab) c
7. สมบัติการมีเอกลักษณ์การคูณ: a x 1 = a = 1 x a โดยที่เราเรียก 1 ว่าเอกลักษณ์ของการคูณ
8. สมบัติการมีอินเวอร์สของการคูณ: a a-1 = 0 = a-1 a โดยที่ a-1 เป็นอินเวอร์สการคูณของ a
9. สมบัติการแจกแจงทางซ้าย: a(b + c) = ab + ac
นอกจากสมบัติของจำนวนจริงแล้ว เรายังมีทฤษฎีบทเบื้องต้นสำหรับจำนวนจริงด้วย ในทำนองเดียวกับสมบัติของจำนวนจริง จะขอนำเสนอเฉพาะส่วนที่คิดว่าสำคัญเท่านั้นนะครับ
ถ้าให้ a, b, c และ d เป็นจำนวนจริงใดๆ จะได้ว่า
1. ถ้า a+c = b+c แล้ว a = b
2. ถ้า c ไม่เท่ากับศูนย์ และ ac =ab แล้ว a = b
3. เมื่อ c > 0 แล้วจะได้ว่า
(1) ถ้า a > b แล้ว ac > bc
(2) ถ้า a < b แล้ว ac < bc
(3) ถ้า ac > bc แล้ว a > b
(4) ถ้า ac < bc แล้ว a < b
4. เมื่อ c < 0 แล้วจะได้ว่า
(1) ถ้า a > b แล้ว ac < bc
(2) ถ้า a < b แล้ว ac > bc
(3) ถ้า ac > bc แล้ว a < b
(4) ถ้า ac < bc แล้ว a > b
5. ถ้า ab = 0 แล้ว a = 0 หรือ b = 0
6. ถ้า a < b และ c < d แล้ว a – d < b – c
การนำสมบัติของจำนวนจริงไปใช้ในการแก้สมการกำลังสอง
ตัวแปร : อักษรภาษาอังกฤษตัวเล็ก เช่น x , y ที่ใช้เป็นสัญลักษณ์
แทนจำนวน
ค่าคงตัว : ตัวเลขที่แททนจำนวน เช่น 1, 2
นิพจน์ : ข้อความในรูปสัญลักษณื เช่น 2, 3x ,x-8 ,
เอกนาม : นิพจน์ที่เขียนอยู่ในรูปการคูณของค่าคงตัวแปรตั้งแต่หนึ่งตัวขึ้นไป
ที่มีเลขชี้กำลังของตัวแปรเป็นจำนวนเต็มบวกหรือศูนย์
เช่น -3, 5xy , 2y
พหุนาม : นิพจน์ที่สามารถเขียนในรูปของเอกนาม หรือการบวกเอกนามตั้งแต่ สองเอกนามขึ้นไป เช่น 3x , 5x +15xy+10x+5
ดีกรีของเอกนาม : ดีกรีสูงสุดของเอกนามในพหุนามนั้น เช่น x+2xy+1 เป็น
พหุนามดีกรี 3
การแยกตัวประกอบของพหุนาม
พหุนามดีกรีสองตัวแปรเดียว : พหุนามที่เขียนได้ในรูป ax + bx +c = 0 เมื่อค่าคงตัวที่ a ≠ 0 และ xเป็นตัวแปร
– การแยกตัวประกอบของ x +bx +c = 0 เมื่อ b , c เป็นค่าคงตัวที่ c = 0
ทำได้โดยการาจำนวน d และ e ที่ de = c และ d+c = b ทำให้ x +bx + c = (x+d)(x+c)
เช่น จงแยกตัวประกอบของ x +7x + 12
จัดพหุนามให้อยู่ในรูป x +(d+e)x+de
นั้นคือ หาจำนวนสองจำนวนที่คูณกันได้ 10 และบวกกันได้ 7
ซึ่งก็คือ 5 และ 2
จะได้ (5)(2) = 10 และ5+2 = 7
ดั้งนั้น x+7x+10= (x+5) (x+2)






