มาเรียนเลขเรื่อง ความสัมพันธ์และฟังก์ชัน(Relations and Functions)
-
การบวก การลบ การคูณ การหาร และการคูณด้วยจำนวนจริงของฟังก์ชัน
| • สมบัติการเ่ท่ากันของจำนวนจริง | ||||
|
กำหนด a, b, c เป็นจำนวนจริงใดๆ |
||||
| 1. สมบัติการสะท้อน a = a | ||||
| 2. สมบัติการสมมาตร ถ้า a = b แล้ว b = a | ||||
| 3. สมบัติการถ่ายทอด ถ้า a = b และ b = c แล้ว a = c | ||||
| 4. สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว a + c = b + c | ||||
| 5. สมบัติการคูณด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว ac = bc | ||||
| • สมบัติการบวกในระบบจำนวนจริง | ||||
| กำหนด a, b, c เป็นจำนวนจริงใดๆ | ||||
|
1. สมบัติปิดการบวก a + b เป็นจำนวนจริง |
||||
|
2. สมบัติการสลับที่ของการบวก a + b = b + c |
||||
|
3. สมบัติการเปลี่ยนกลุ่มการบวก a + ( b + c) = ( a + b ) + c |
||||
|
4. เอกลักษณ์การบวก 0 + a = a = a + 0 |
||||
|
นั่นคือ ในระบบจำนวนจริงจะมี 0 เป็นเอกลักษณ์การบวก |
||||
|
5. อินเวอร์สการบวก a + ( -a ) = 0 = ( -a ) + a |
||||
|
นั่นคือ ในระบบจำนวนจริง จำนวน a จะมี -a เป็นอินเวอร์สของการบวก |
||||
|
• สมบัติการคูณในระบบจำนวนจริง |
||||
|
กำหนดให้ a, b, c, เป็นจำนวนจริงใดๆ |
||||
|
1. สมบัติปิดการคูณ ab เป็นจำนวนจริง |
||||
|
2. สมบัติการสลับที่ของการคูณ ab = ba |
||||
|
3. สมบัติการเปลี่ยนกลุ่มของการคูณ a(bc) = (ab)c |
||||
|
4. เอกลักษณ์การคูณ 1 · a = a = a · 1 |
||||
|
นั่นคือในระบบจำนวนจริง มี 1 เป็นเอกลักษณ์การคูณ |
||||
|
5. อินเวอร์สการคูณ a · a-1 = 1 = a · a-1, a ≠ 0 |
||||
|
นั่นคือ ในระบบจำนวนจริง จำนวนจริง a จะมี a-1 เป็นอินเวอร์สการคูณ ยกเว้น 0 |
||||
|
6. สมบัติการแจกแจง |
||||
|
a( b + c ) = ab + ac |
||||
|
( b + c )a = ba + ca |
||||
| จากสมบัติของระบบจำนวนจริงที่ได้กล่าวไปแล้ว สามารถนำมาพิสูจน์เป็นทฤษฎีบทต่างๆ ได้ดังนี้ | ||||
| ทฤษฎีบทที่ 1 | กฎการตัดออกสำหรับการบวก | |||
| เมื่อ a, b, c เป็นจำนวนจริงใดๆ | ||||
|
ถ้า a + c = b + c แล้ว a = b |
||||
|
ถ้า a + b = a + c แล้ว b = c |
||||
| ทฤษฎีบทที่ 2 | กฎการตัดออกสำหรับการคูณ | |||
| เมื่อ a, b, c เป็นจำนวนจริงใดๆ | ||||
| ถ้า ac = bc และ c ≠ 0 แล้ว a = b | ||||
| ถ้า ab = ac และ a ≠ 0 แล้ว b = c | ||||
| ทฤษฎีบทที่ 3 | เมื่อ a เป็นจำนวนจริงใดๆ | |||
| a · 0 = 0 | ||||
| 0 · a = 0 | ||||
| ทฤษฎีบทที่ 4 | เมื่อ a เป็นจำนวนจริงใดๆ | |||
| (-1)a = -a | ||||
| a(-1) = -a | ||||
| ทฤษฎีบทที่ 5 | เมื่อ a, b เป็นจำนวนจริงใดๆ | |||
| ถ้า ab = 0 แล้ว a = 0 หรือ b = 0 | ||||
| ทฤษฎีบทที่ 6 | เมื่อ a เป็นจำนวนจริงใดๆ | |||
|
a(-b) = -ab |
||||
| (-a)b = -ab | ||||
| (-a)(-b) = ab | ||||
| เราสามารถนิยามการลบและการหารจำนวนจริงได้โดยอาศัยสมบัติของการบวกและการคูณใน ระบบจำนวนจริงที่ได้กล่าวไปแล้วข้างต้น |
||||
| • การลบจำนวนจริง | ||||
| บทนิยาม | เมื่อ a, b เป็นจำนวนจริงใดๆ | |||
| a- b = a + (-b) | ||||
| นั่นคือ a – b คือ ผลบวกของ a กับอินเวอร์สการบวกของ b | ||||
| • การหารจำนวนจริง | ||||
| บทนิยาม | เมื่อ a, b เป็นจำนวนจริงใดๆ เมื่อ b ≠ 0 | |||
|
||||
|
||||
ฟังก์ชันประกอบ
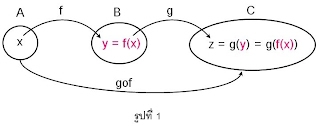
Dg ต้องไม่เท่ากับ Ø จากแผนภาพจะพบว่า
f เป็นความสัมพันธ์จาก A → B
g เป็นความสัมพันธ์จาก B → C
gof เป็นความสัมพันธ์จาก A → C การหาฟังก์ชันประกอบ จากแผนภาพการแจกแจงสมาชิกของฟังก์ชันทำได้ ดังตัวอย่างที่ 1