สรุปเนื้อหาเรื่อง เรขาคณิตวิเคราะห์และภาคตัดกรวย เรื่องวงรี (Ellipse) ม.4
สรุปเนื้อหาเรื่อง
- เส้นขนานและเส้นตั้งฉาก
- ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
- ภาคตัดกรวย (conic section หรือ conic)
- วงกลม
- สมการวงกลม
- วงรี
- สมการวงรี
- พาราโบลา
- ไดเรกตริกซ์
- สมการพาราโบลา
นิยามสมการวงรี
วงรี (Ellipse) คือเซตของจุดทั้งหมดในระนาบซึ่งผลบวกของระยะทางจากจุดใดๆจุดหนึ่งในเซตไปยังจุดคงที่ 2 จุดมีค่าคงตัว
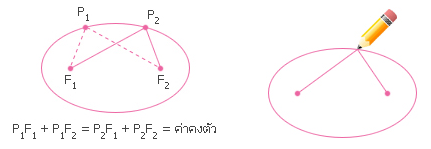
จากบทนิยามนี้ มีวิธีง่ายๆ ในการวาดรูปวงรี (ดูรูปที่ 2) วางกระดาษบนกระดานวาดรูปปักหมุด 2 ตัวที่จุดต่างกัน ใช้เป็นโฟกัสของวงรี ตัดเชือกเส้นหนึ่งยาวกว่าระยะทางระหว่างหมุดทั้งสอง ผูกปลายเชือกแต่ละข้างกับหมุด โดยใช้ดินสอรั้งเชื่อให้ตึงตลอดเวลา ขณะที่ค่อยๆ เคลื่อนดินสอรอบโฟกัส รอยดินสอที่เกิดขึ้นจะเป็นรูปวงรีเพราะผลบวกของระยะทางจากจุดปลายดินสอถึงโฟกัสทั้งสองเท่ากับความยาวของเชือกที่มีความยาวคงตัวเสมอ
ถ้าเชือกยาวกว่าระยะห่างระหว่างโฟกัสเพียงเล็กน้อย วงรีที่วาดได้จะมีรูปร่างเรียวยาว ดังเช่นในรูปที่ 3ก แต่ถ้าโฟกัสอยู่ใกล้กันเมื่อเปรียบเทียบกับความยาวของเชือก (เชือกยาวกว่าระยะห่างระหว่างโฟกัสมาก) วงรีที่วาดได้จะเกือบกลม ดังเช่นในรูปทางขวา ยิ่งถ้าจุดโฟกัสใกล้กันเท่าไหร่ ก็จะยิ่งกลมขึ้นๆ

ส่วนประกอบของวงรี
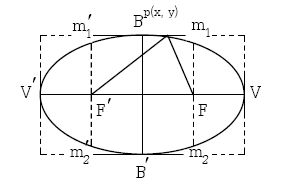
F, F’ เป็นจุดคงที่ เรียกว่าจุดโฟกัส (Focus)
V, V’ เป็นเส้นตรงที่ผ่านจุดโฟกัส และมีจุดปลายทั้งสองเป็นจุดยอด เรียกว่า แกนนอก
B, B’ เป็นเส้นตรงที่ผ่านจุดศูนย์กลางและตั้งฉากกับแกนเอก โดยมีจุดปลายทั้งสองอยู่บนวงรี เรียกว่า แกนโท
m1m2, m1‘m2‘ เป็นเส้นตรงที่ผ่านจุดโฟกัส และตั้งฉากกันแกนของรูป เรียกว่าเส้นลาตัสเรกตัม
วงรีที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)
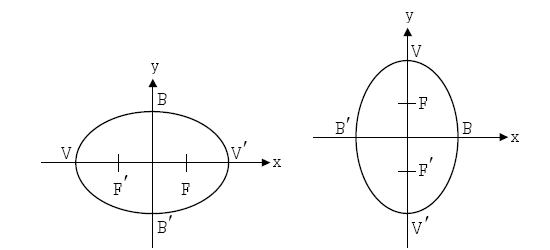
วงรีที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิดและแกนเอกอยู่บนพิกัด

สรุปสมการวงรี
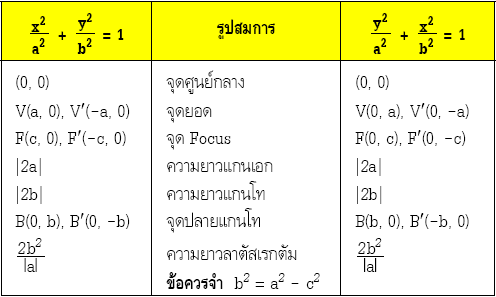

ขอบคุณข้อมูล https://www.tewfree.com/






