เนื้อหา เรื่องจำนวนเชิงซ้อน
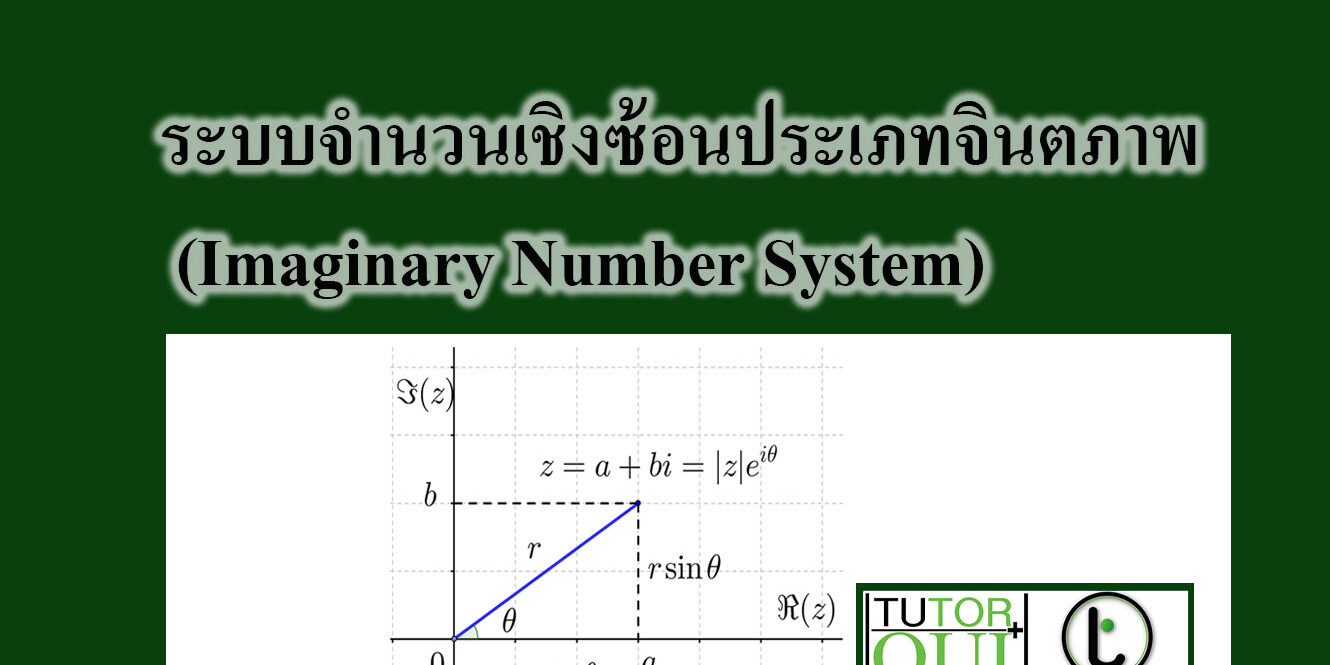
ระบบจำนวนเชิงซ้อนประเภทจินตภาพ (Imaginary Number System)
จำนวนเชิงซ้อน(Complex Number)
ระบบจำนวนเลขเท่าที่มนุษย์คิดค้นพบในขณะนี้ประกอบด้วยเลขจำนวน 2 ระบบคือ
1.ระบบจำนวนจริง (Real Number System)
2.ระบบจำนวนเชิงซ้อนประเภทจินตภาพ (Imaginary Number System)
สรุปเป็นแผนภูมิได้ดังนี้
จำนวนเชิงซ้อน
ระบบจำนวนจริงระบบจำนวนจินตภาพ
จำนวนตรรกยะจำนวนอตรรกยะ
จำนวนเต็มจำนวนเศษส่วน
จำนวนเต็มลบจำนวนเต็มศูนย์จำนวนเต็มบวก
1.จำนวนจินตภาพ(Imaginary Number)เป็นจำนวนที่เกิดจากนักคณิตศาสตร์
พยายามแก้ไขปัญหาในค่าx จากสมการx2 + 1 = 0
x2=-1
x=±Ö- 1
แต่เนื่องจากÖ- 1มิใช่จำนวนจริงนักคณิตศาสตร์จึงตั้งชื่อจำนวนจริงลบที่อยู่ในเครื่องหมายÖว่าจำนวนจินตภาพและใช้สัญลักษณ์iแทนÖ-1
ดังนั้นi2=-1
2.จำนวนตรรกยะ(Rational Number) คือจำนวนที่สามารถเขียนในรูปเศษส่วน
a/b เมื่อa และbเป็นจำนวนเต็มโดยที่b ¹0จำนวนตรรกยะจำแนกได้เป็น 3 ประเภทใหญ่ๆคือ
1.จำนวนเต็ม(Integer)
2.เศษส่วน(Fraction)
3.ทศนิยม(Repeating decimal)
3.จำนวนอตรรกยะ(irrational Number) คือจำนวนที่ไม่สามารถเขียนในรูปเศษ
ส่วนa/b เมื่อa และbเป็นจำนวนเต็มโดยที่b ¹0หรือจำนวน
อตรรกยะคือจำนวนที่ไม่ใช่จำนวนตรรกยะนั่นเองจำนวนอตรรกยะจำแนกได้เป็น 2 ประเภทใหญ่ใหญ่คือ
1.จำนวนติดกรณ์บางจำนวนเช่นเป็นต้น
2.จำนวนทศนิยมไม่ซ้ำเช่น 5.18118168473465
หมายเหตุpซึ่งประมาณได้ด้วย 22/7 แต่จริงๆแล้วpเป็นเลข
อตรรกยะ
สิ่งที่ควรทราบ
จำนวนจริงทุกจำนวนสามารถแทนได้ด้วยจุดบนเส้นจำนวน
4.จำนวนเชิงซ้อน(Complex Number)เขียนแทนด้วยz โดยที่z = (a,b)
จะได้ว่าz=a + biเมื่อi=Ö-1i2 = -1
เรียก a ว่าเป็นส่วนจำนวนจริงของจำนวนเชิงซ้อนz
b ว่าเป็นส่วนจินตภาพของจำนวนเชิงซ้อนz
4.1การเท่ากันของจำนวนเชิงซ้อน
ให้z1 = a + biและz2=c + di
ดังนั้นz1=z2ก็ต่อเมื่อa = cและb = d
4.2การบวกจำนวนเชิงซ้อน
ให้z1 = a + biและz2=c + di
ดังนั้นz1 + z2=(a+c) + (b+d)i
4.3การคูณจำนวนเชิงซ้อนด้วยจำนวนจริง
ให้z1 = a + biและkเป็นจำนวนจริง
kz=ka + kbi
4.4การคูณจำนวนเชิงซ้อนด้วยจำนวนเชิงซ้อน
ให้z1 = a + biและz2=c + di
z1 z2 = (a + bi)( c + di)=(ac – bd , ad+bc)
ตัวอย่างจงหาผลคูณของ3 + 4iกับ2 + i
วิธีทำ(3 + 4i)( 2 + i )=6 +3i + 8i + 4i2
=6 + 11i – 4=2 + 11i
4.5คอนจูเกต(conjugate) ของจำนวนเชิงซ้อนแทนด้วยz
ถ้าz = a + biแล้วz=a – bi