ลำดับและอนุกรม (คณิตศาสตร์พื้นฐาน ม.5 บทที่ 1)

บทที่ 1. ลำดับและอนุกรม
1. ลำดับ
· ความหมายของลำดับ
· การหาพจน์ทั่วไปของลำดับ
· ลำดับเลขคณิต
· ลำดับเรขาคณิต
2. อนุกรม
3. อนุกรมเลขคณิต
4. อนุกรมเรขาคณิตบทที่

1. ลำดับและการเขียนลำดับ

ลำดับ (Sequences) หมายถึง ตัวเลขชุดหนึ่งที่เขียนเรียงกันภายใต้กฎเกณฑ์ที่กำหนดให้

นิยาม : ฟังก์ชันที่มีโดเมน (Domain) (สมาชิกตัวหน้า) เป็นเซตของจำนวนเต็มบวกที่เรียงจากน้อยไปมากโดยเริ่มตั้งแต่ 1 และมีเรนจ์ (Range) (สมาชิกตัวหลัง) เป็นเซตของจำนวนจริง

แบ่งออกเป็น 2 ชนิด คือ

1. ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก { 1, 2, 3,4 …, n } เรียกว่า ลำดับจำกัด (Finite Sequence)

2. ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก { 1, 2, 3,4 … } เรียกว่า ลำดับอนันต์ (Infinite Sequence)

โดยทั่วไปแล้วการเขียนฟังก์ชันเรามักจะใช้ตัว f, g ,h เป็นตัวบอกฟังก์ชัน แต่สำหรับลำดับ จะใช้ตัว a ในการเขียนแทน นั่นคือ a(x) หรือสามารถเขียนแทนได้ด้วย ax เช่น a(1) แทนด้วย a1 , a(n) แทนด้วย an เป็นต้น

การหาพจน์ทั่วไปของลำดับ

เมื่อกำหนดให้ การหาพจน์ทั่วไปหรือพจน์ที่ n ของลำดับ เป็นการเขียนลำดับโดยแสดงพจน์ทั่วไป (พจน์ที่ n )ที่มีพจน์ n เป็นตัวแปรและเมื่อแทน n ด้วยจำนวนเต็มบวก 1,2,3,….. แล้วจะได้พจน์ต่างๆ ตรงกับพจน์ของลำดับที่กำหนดให้ การหาพจน์ทั่วไปของลำดับดังกล่าวแล้ว ทำได้โดยหาความสัมพันธ์ของพจน์กับตำแหน่งที่หรือลำดับที่ของพจน์นั้นๆ ดังตัวอย่างต่อไปนี้

ในการกำหนดลำดับอนันต์จะเขียนพจน์ทั่วไปกำกับไว้กับการเขียนลำดับด้วยเสมอ ทั้งนี้ เพื่อให้เกิดความชัดเจนว่า ต้องการกล่าวถึงลำดับใด เพราะลำดับที่แตกต่างกันอาจจะมีพจน์แรกๆ เหมือนกันก็ได้ ดังนั้น การเขียนลำดับอนันต์โดยเขียนเฉพาะพจน์แรกๆ 3-4 พจน์จึงไม่เพียงพอ ยกเว้นกรณีที่ระบุได้ว่าลำดับอนันต์มีลักษณะเฉพาะเป็นที่ทราบกันแล้วว่าจะหาพจน์ถัดจากพจน์แรกๆ ได้อย่างไร เช่น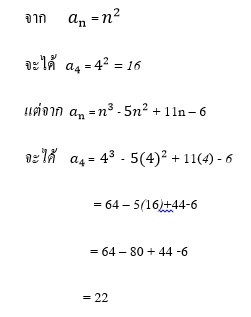