บทนิยาม ลอการิทึม (logarithm) -คณิตศาสตร์ม.ปลาย

ลอการิทึม (logarithm) คือ

บทนิยาม

ถ้า a > 0 และ a ไม่เท่ากับ 1 เรียกฟังก์ชัน {(x,y) I x = a^y} ว่าฟังก์ชันลอการิทึม

นิยมเขียน y = log_a x แทน x = a^y

“ log_a x” อ่านว่า ล็อกเอกซ์ฐานเอ

ดังนั้นอาจเขียนแทนฟังก์ชันลอการิทึมด้วย

y = log_a x , a > 0 , a ไม่เท่ากับ 1

นิยามฟังก์ชั่นลอการิทึม

สรุปได้ว่า ตัวเลขหลัง log ต้องเป็นจำนวนจริงบวก

ฐานของ log ต้องเป็นเลขจำนวนจริงบวกแต่ไม่เป็น1

ค่าของ log คือ y เป็นจำนวนจริงบวกจำนวนจริงลบหรือศูนย์ก็ได้

log_ax อ่านว่า “ลอการิทึมเอกซ์ฐานเอ” หรือ“ลอกเอ็กซ์ฐานเอ” เนื่องจากf (ฟังก์ชันเอกซ์โพเนนเซียล) เป็นฟังก์ชัน 1 –1

ดังนั้น f^-1จึงเป็นฟังก์ชันและเป็นฟังก์ชัน 1-1ด้วย

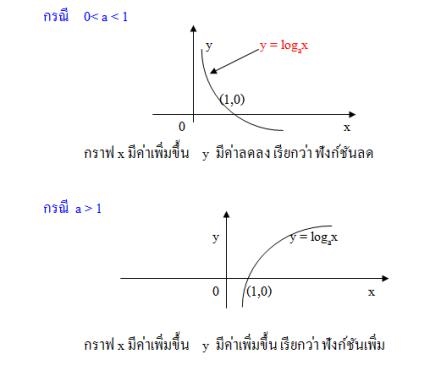
แก้สมการลอการิทึม

1.log_a x = log_a y → x = y (ฐานเท่า → หลัง log เท่า)
2.log_a x = log_b x → x = 1(ฐานไม่เท่า, หลัง log เท่า → log_a 1= 0)
3.ฐานไม่เท่า, หลัง log ไม่เท่า → วาดกราฟ
4.ตรวจคำตอบทุกครั้ง หลัง log > 0

ฐาน log > 0, ไม่เท่ากับ 1

logarithm คือฟังก์ชันที่อยู่ในรูป {(x, y) ∈ $\mathbb{R}^+\times \mathbb{R}$ : $ฟังก์ชันลอการิทึม$ } โดยที่ a เป็นจำนวนจริงที่มากกว่า 0 และ a ≠ 1