การดำเนินการเวกเตอร์

การดำเนินการเวกเตอร์

การดำเนินการพีชคณิต

พื้นฐานพีชคณิต (ไม่ใช่การหาอนุพันธ์) การดำเนินการในแคลคูลัสเวกเตอร์จะเรียกว่าพีชคณิตเวกเตอร์ ถูกกำหนดไว้สำหรับปริภูมิเวกเตอร์และได้ถูกนำไปประยุกต์ใช้กันทั่วโลกกับสนามเวกเตอร์และประกอบด้วย

• การคูณสเกลาร์ การคูณของสนามสเกลาร์และสนามเวกเตอร์ย่อมได้สนามเวกเตอร์ ;
• การบวกเวกเตอร์ การบวกของสนามเวกเตอร์สองสนามย่อมได้สนามเวกเตอร์ ;
• ผลคูณจุด การคูณของสนามเวกเตอร์สองสนามย่อมได้สนามสเกลาร์ ;
• ผลคูณไขว้ การคูณของสนามเวกเตอร์สองสนามย่อมได้สนามเวกเตอร์ ;

นอกจากนี้ยังมีผลคูณเชิงเวกเตอร์ของสามเวกเตอร์ 2 แบบ คือ:

ผลคูณเชิงสเกลาร์สามชั้น

ผลคูณจุดของผลคูณเวกเตอร์และผลคูณไขว้ของ 2 เวกเตอร์: ;

ผลคูณเชิงเวกเตอร์สามชั้น

ผลคูณไขว้ของผลคูณเวกเตอร์และผลคูณไขว้ของ 2 เวกเตอร์:  or ;

แม้ว่าสิ่งเหล่านี้จะเป็นการดำเนินการพื้นฐานที่มักจะถูกนำมาใช้น้อยกว่า, ดังเช่นที่สามารถแสดงได้ในแง่ของผลคูณจุดและผลคูณไขว้ก็ตาม

เวกเตอร์ ปริมาณมี 2 แบบ คือสเกลาร์ กับเวกเตอร์
สเกลาร์ เป็น ปริมาณที่มีแต่ขนาด เช่น พื้นที่ อุณหภูมิ ความยาว เป็นต้น
เวกเตอร์ เป็น ปริมาณที่มีทั้งขนาดและทิศทาง เช่นความเร็ว แรง เป็นต้น
เราสามารถแทนเวกเตอร์ในเชิงเรขาคณิตได้ด้วยส่วนของเส้นตรงและลูกศร โดยที่ทิศทางของลูกศรแทนทิศทางของเวกเตอร์ และความยาวของลูกศรแทน ขนาดของเวกเตอร์ หางลูกศรเรียกว่า จุดเริ่มต้นของเวกเตอร์ หัวลูกศร เรียกว่า จุดสิ้นสุดของเวกเตอร์

สัญลักษณ์ที่ใช้

(รูปที่ 1)

บทนิยาม  1  ถ้าเวกเตอร์  u และ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ แล้ว ผลบวกของเวกเตอร์  u และ v เขียนแทนด้วยเวกเตอร์  u + v  หาได้จากให้ตำแหน่งเวกเตอร์ v มีจุดเริ่มต้นอยู่ที่จุดสิ้นสุดของเวกเตอร์ u
เวกเตอร์ u + v  จะแทนด้วยลูกศรจากจุดเริ่มต้นของเวกเตอร์ u  ไปยังจุดสิ้นสุดของเวกเตอร์  v ดังรูปที่  2

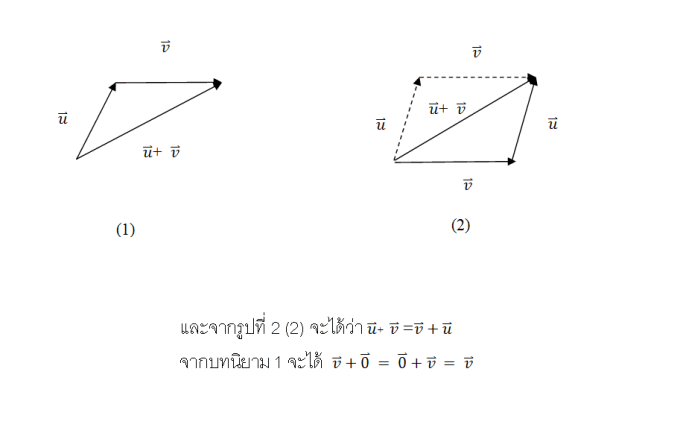(รูปที่ 2)

บทนิยาม 2 ให้เวกเตอร์ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ และ k เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ แล้ว เวกเตอร์  kv หมายถึงเวกเตอร์ที่มีขนาดเท่ากับ |k| เท่าของเวกเตอร์ v เมื่อ k>0 เวกเตอร์ kv จะมีทิศทางเดียวกับ v และเมื่อ k<0 เวกเตอร์ kv มีทิศตรงข้ามกับเวกเตอร์ v และให้เวกเตอร์  kv =0 เมื่อ k =0

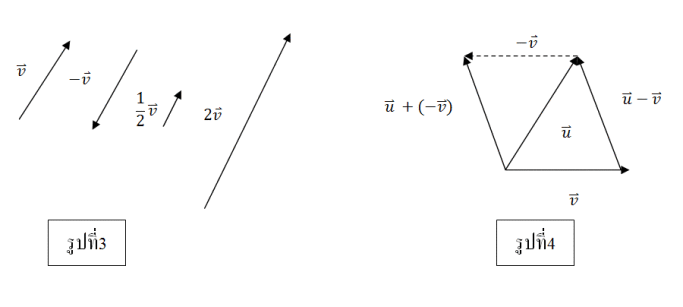จากรูปที่  3 ได้ว่าเวกเตอร์  v กับเวกเตอร์  Kv เป็นเวกเตอร์ที่ขนานกัน

เวกเตอร์ในระบบพิกัดฉากในปริภูมิสามมิติ

            ให้เวกเตอร์ v เป็นเวกเตอร์ในปริภูมิ 3 มิติในระบบพิกัดฉาก ซึ่งมีจุดเริ่มต้นอยู่ที่จุดกำเนิด และจุดสิ้นสุดอยู่ที่จุด (x₁,y₁,z₁) ดังรูปที่ 5 เรียกพิกัด x₁,y₁และ z₁ว่า ส่วนประกอบเวกเตอร์ และเขียนแทนด้วย

 

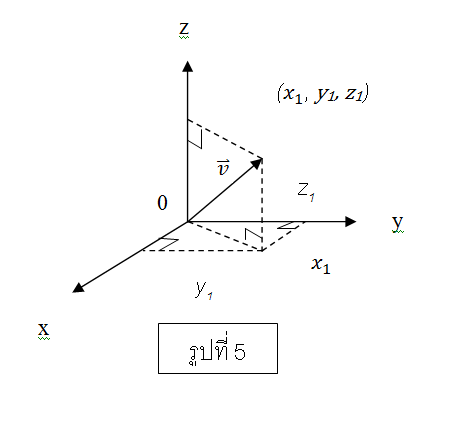
การรวมเวกเตอร์ หมายถึง การบวกหรือลบกันของเวกเตอร์ตั้งแต่ 2 เวกเตอร์ ขึ้นไป ผลลัพธ์ที่ได้เป็นปริมาณเวกเตอร์ เรียกว่า เวกเตอร์ลัพธ์ (Resultant Vector) ซึ่งพิจารณาได้ ดังนี้

1.1 การบวกเวกเตอร์โดยวิธีการเขียนรูป ทำได้โดยเขียนเวกเตอร์ที่เป็นตัวตั้ง จากนั้นเอาหางของเวกเตอร์ที่เป็นผลบวกหรือผลต่าง มาต่อกับหัวของเวกเตอร์ตัวตั้ง โดยเขียนให้ถูกต้องทั้งขนาดและทิศทาง เวกเตอร์ลัพธ์หาได้โดยการวัดระยะทาง จากหางเวกเตอร์แรกไปยังหัวเวกเตอร์สุดท้าย

จากรูป เวกเตอร ์  = 

1.2 การบวกเวกเตอร์โดยใช้วิธีการทางคณิตศาสตร์

ให้ เวกเตอร์ ทำมุมกับ เป็นมุม q คำนวณหาเวกเตอร์ลัพธ์ได้ ดังนี้

ขนาดของเวกเตอร์ลัพธ์คำนวณได้จากกฎของโคไซน์

ทิศทางของเวกเตอร์ลัพธ์หาได้จาก

a =  …………………………………………………..(2)

หรือหาได้จากกฎของไซน์ ดังนี้

 =  =  ……………………………………………….(3)

ข้อสังเกต จากสมการที่ (1) พบว่า

1. เมื่อ q = (คือ และ อยู่ในทิศทางเดียวกัน) จะได้ขนาดของ = โดยทิศทางของ มีทิศเดียวกับ และ 
2. เมื่อ q = 
   2.1 ถ้า > จะได้ = – และ มีทิศเดียวกับ 
   2.2 ถ้า < จะได้ = – และ มีทิศเดียวกับ 

3. เมื่อ q = จะได้

ขนาด R = และ a = 

1.3 การลบเวกเตอร์

การลบเวกเตอร์ สามารถหาเวกเตอร์ลัพธ์ได้เช่นเดียวกับการบวกเวกเตอร์ แต่ให้กลับทิศทางของเวกเตอร์ตัวลบ ดังนี้

 ………………………..(4)

2. เวกเตอร์หนึ่งหน่วย (Unit Vector)

เวกเตอร์หนึ่งหน่วย หมายถึง เวกเตอร์ที่มีขนาดหนึ่งหน่วยในทิศทางใดๆ เช่น เวกเตอร์ สามารถเขียนได้ด้วยขนาดของ คูณกับเวกเตอร์หนึ่งหน่วย ซึ่งมีทิศทางเดียวกับ คือ

 = 

หรือ  =  ……………………………………………..(5)

โดย คือ เวกเตอร์หนึ่งหน่วยที่มีขนาดหนึ่งหน่วยและทิศเดียวกันกับ 

ในระบบแกนมุมฉาก เวกเตอร์หนึ่งหน่วยบนแกน x , y และ z แทนด้วยสัญลักษณ์ , และ ตามลำดับ จะได้

 =  ;  =  ;  =  …………………………(6)

เมื่อ  คือ เวกเตอร์ที่มีขนาดเท่ากับ มีทิศทางตามแนวแกน x

 คือ เวกเตอร์ที่มีขนาดเท่ากับ มีทิศทางตามแนวแกน y

 คือ เวกเตอร์ที่มีขนาดเท่ากับ มีทิศทางตามแนวแกน z

3. เวกเตอร์องค์ประกอบ (Component Vector)

3.1 องค์ประกอบของเวกเตอร์ใน 2 มิติ

ถ้า อยู่ในระนาบ x , y โดย ทำมุม q กับแกน x

องค์ประกอบของ ตามแกน x คือ โดย = Acosq

องค์ประกอบของ ตามแกน y คือ โดย = Asinq

ดังนั้น เวกเตอร์ เขียนแยกเป็นองค์ประกอบได้ ดังนี้

 =+   ……………………….(7)

หรือ

 = Acosq + Asinq 

โดยที่ ขนาดของ 

 =  ……………………………(8)

3.2 องค์ประกอบของเวกเตอร์ใน 3 มิติ

กำหนดให้ อยู่บนระนาบ x , y ,z โดยเวกเตอร์ ทำมุมกับแกน x , y , z เป็นมุม q _x , q _y , q _z

ตามลำดับ เวกเตอร์ สามารถแยกเป็นองค์ประกอบตามแกน x , y , z ได้ ดังนี้

ขนาดของ  แทนด้วย A_x = Acosq _x โดยที่ cosq _x = 

ขนาดของ แทนด้วย A_y = Acosq _y โดยที่ cosq _y = 

ขนาดของ แทนด้วย A_z = Acosq _z โดยที่ cosq _z = 

ดังนั้น  = 

 = 

ขนาด  คือ

A =  …………………………………(9)

ทิศทางของเวกเตอร์ คือ มุมที่ ทำกับแกน x , y , z หาได้จาก

 :  : 

4. เวกเตอร์ตำแหน่ง (Position Vector)

เวกเตอร์ตำแหน่ง หมายถึง เวกเตอร์ที่บอกตำแหน่งของวัตถุเทียบกับจุดใดจุดหนึ่ง เรียกว่า จุดอ้างอิง

จากรูป เวกเตอร์ และ เป็นเวกเตอร์บอกตำแหน่งของจุด P และ Q เทียบกับจุด O ในระบบพิกัด โดย

จะได้

โดยขนาดของ คือ

……………………………….(11)

ทิศทางของ หาได้จาก

; ;  …… (12)

5. การคูณเวกเตอร์ มี 2 แบบ ดังนี้

5.1 ผลคูณสเกลาร์ (Scalar product หรือ dot product แทนด้วยเครื่องหมาย ” . ” )

กำหนดให้ ทำมุม กับ ผลคูณสเกลาร์ของเวกเตอร์ทั้งสองมีนิยาม ดังนี้

โดยที่ A และ B เป็นขนาดของเวกเตอร์ และ ตามลำดับ

 คือ มุมระหว่างเวกเตอร์ A กับ B

คุณสมบัติของผลคูณแบบสเกลาร์

ถ้า , , เป็นเวกเตอร์ใดๆ และ , , เป็น unit vector ในแนวแกน x , y ,z จะได้ว่า

คุณสมบัติของผลคูณแบบสเกลาร์

ถ้า , , เป็นเวกเตอร์ใดๆ และ , , เป็น unit vector ในแนวแกน x , y , z จะได้ว่า

1. 

2. 

3. 

4. 

5. 

6. 

7. 

โดยที่ 

ผลคูณเวกเตอร์ (Vector Product หรือ Cross Product แทนด้วยเครื่องหมาย “x” )

กำหนดให้ และ เป็นเวกเตอร์ที่ทำมุม q ต่อกัน และ เป็นเวกเตอร์ลัพธ์ โดย

ขนาดของ มีนิยามว่า 

ทิศทางของ หาได้โดยใช้กฎมือขวา โดยปลายนิ้วทั้งสี่แทนทิศทางของ และหมุนไปหา จะได้นิ้วหัวแม่มือแทนทิศทางของ 

คุณสมบัติของผลคูณแบบเวกเตอร์

1. 

2. 

3. 

4. 

5. 

หรือเขียนในรูปของดีเทอร์มิแนนท์ (Determinant) ได้ว่า

โดยที่

6. การหาอนุพันธ์ของเวกเตอร์

ถ้าเวกเตอร์ , และ เป็นฟังก์ชันของตัวแปรอิสระ U ดังนั้น จะได้

1. 

2. 

3. 

4. 

5.