คณิตศาสตร์เชิงการจัด การเรียงสับเปลี่ยน และ การจัดหมู่ คณิตศาสตร์ ม.ปลาย

คณิตศาสตร์เชิงการจัด (combinatorics) คือสาขาหนึ่งของคณิตศาสตร์ ที่ศึกษากลุ่มของวัตถุจำนวนจำกัดที่มีคุณสมบัติสอดคล้องกับเงื่อนไขบางประการ และมักสนใจเป็นพิเศษที่จะ “นับ” จำนวนวัตถุในกลุ่มนั้น ๆ (ปัญหาการแจกแจง) หรืออาจหาคำตอบว่า วัตถุที่มีคุณสมบัติที่ต้องการนั้นมีอยู่หรือไม่ (ปัญหาสุดขอบ) การศึกษาเกี่ยวกับการนับวัตถุ บางครั้งถูกจัดให้อยู่ในสาขาความน่าจะเป็นแทน

มาดูเรื่อง การเรียงสับเปลี่ยน และ การจัดหมู่

การจัดหมู่ คือ การเลือกวัตถุจากกลุ่ม โดยไม่สนใจลำดับของการเลือก เช่น ในการเล่นไพ่โป๊กเกอร์ ผู้เล่นแต่ละคนจะได้รับไพ่ 5 ใบจากทั้งหมด 52 ใบ ซึ่งลำดับในการได้รับแต่ละใบมานั้นจะไม่มีผลในการเล่น

ในคณิตศาสตร์เชิงการจัดนั้น การจัดหมู่ คือ สับเซต ในเซตใดๆ นั้น ตำแหน่งไม่มีความสำคัญ เนื่องจากในแต่ละเซต สิ่งที่เราสนใจคือ สิ่งของ ที่อยู่ในเซต หรือสมาชิกของเซต แต่ไม่สนใจลำดับ เช่น

{8, 4, 3} = {3, 4, 8}

และ {1,1,1} มีความหมายเท่ากับ {1} เนื่องจาก เซตนั้นกำหนดความแตกต่างด้วยสมาชิกที่แตกต่างกันในเซต

ดูเพิ่มที่บทความ การจัดหมู่

สรุปสูตร

การเรียงสับเปลี่ยน แบบเลือกซ้ำได้

การเรียงสับเปลี่ยน แบบไม่มีการเลือกซ้ำ

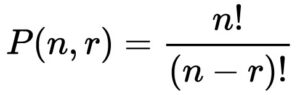การจัดหมู่ แบบเลือกซ้ำได้

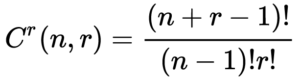การจัดหมู่ แบบไม่มีการเลือกซ้ำ