ฟังก์ชันและกราฟของฟังก์ชัน
ฟังก์ชันและกราฟของฟังก์ชัน มีความเกี่ยวข้องกันเนื่องจากฟังก์ชันที่เราเขียนในรูป y = f(x) สามารถนำไปเขียนกราฟในระบบพิกัดฉากได้ ซึ่งกราฟในระบบพิกัดฉากก็คือ กราฟที่ประกอบไปด้วยแกน x และ แกน y
สมบัติของคู่อันดับ
- (a,b) = (b,a) ก็ต่อเมื่อ a = b
- ถ้า (a,b) = (c,d) แล้วจะได้ a = c และ b = d
- ถ้า (a,b) ≠ (c,d) แล้วจะได้ a ≠ c หรือ b ≠ d
ผลคูณคาร์ทีเซียน
| ผลคูณคาร์ทีเซียนของเซต A และเซต B คือเซตของคู่อันดับ (a,b) ทั้งหมดซึ่ง a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B และเขียนแทนด้วย A× B | |||||
| นั่นคือ A× B = { (a,b) | a ∈ A และ b ∈ B } | |||||
| สมบัติของผลคูณคาร์ทีเซียน | |||||
| กำหนด A, B และ C เป็นเซตใดๆ แล้ว | |||||
| 1. | A× B ไม่จำเป็นต้องเท่ากับ B × A | ||||
| A× B = B × A ก็ต่อเมื่อ A = B หรือ A = Ø หรือ B = Ø | |||||
| A× B ≠ B × A ก็ต่อเมื่อ A ≠ B ≠ Ø | |||||
| 2. | A × Ø = Ø × A = Ø | ||||
| 3. | A × ( B ∪ C ) | = (A× B) ∪(A × C) | |||
| (A ∪ B) × C | = (A× C) ∪(B × C) | ||||
| 4. | A × ( B ∩ C ) | = (A× B) ∩ (A × C) | |||
| (A ∩ B) × C | = (A× B) ∩ (B × C) | ||||
| 5. | A × ( B – C ) | = (A× B) – (A × C) | |||
| (A – B) × C ) | = (A× C) – (B × C) | ||||
ให้ A, B และ C เป็นเซตใด และ n(A) คือ จำนวนสมาชิกของเซต A
- A×{} = {}
- {}×A = {}
- A×(B∪C) = (A×B)∪(A×C)
- A×(B∩C) = (A×B)∩(A×C)
- A×(B-C) = (A×B) – (A×C)
- n(A×B) = n(A).n(B)
รูปแบบของฟังก์ชัน
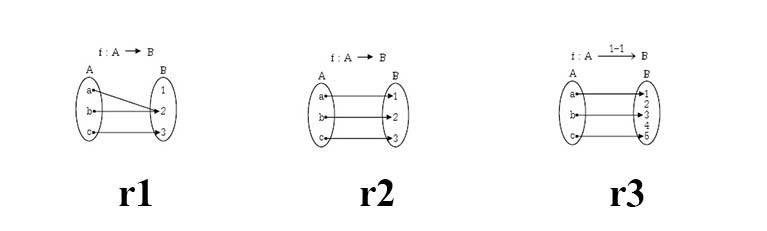
| r1 | ฟังก์ชันจาก A ไป B f เป็นฟังก์ชันจาก A ไป B เขียนแทนด้วย f:A→B หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B |
| r2 | ฟังก์ชันจาก A ไปทั่วถึง B f เป็นฟังก์ชันจาก A ไปทั่วถึง B เขียนแทนด้วย f:A onto→ B หมายความว่า ทุกสมาชิกใน A และ B ต้องมีคู่ |
| r3 | ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B เขียนแทนด้วย f:A 1-1→ B หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B และคู่ไม่ซ้ำ |