ความรู้เบื้องต้นเกี่ยวกับเซต ม.4

เซตพื้นฐาน

เซตเป็นหัวข้อที่มีความสำคัญและแทรกอยู่ในเนื้อหาของคณิตศาสตร์แทบทุกส่วน เราใช้เซตในการรวบรวมสิ่งต่าง ๆ ไม่ว่าจะเป็น ค่าตัวเลข ตัวแปร ที่มีคุณสมบัติเหมือนกันไว้ด้วยกันเป็นประโยชน์ต่อการจำแนกประเภทของสิ่งต่าง ๆ ออกเป็นกลุ่ม

เซต เป็นคำที่ใช้บ่งบอกถึงกลุ่มของสิ่งต่างๆ และเมื่อกล่าวถึงกลุ่มใดแน่นอนว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่ม เช่น

เซตสระในภาษาอังกฤษ หมายถึง กลุ่มของอังกฤษ a, e, i, o และ u

เซตของจำนวนนับที่น้อยกว่า 10 หมายถึง กลุ่มตัวเลข 1,2,3,4,5,6,7,8,และ9

สิ่งที่ในเชตเรียกว่า สมาชิก ( element หรือ members )

เซต ม.4 เซต ก็คือ การบอกลักษณะที่เป็นกลุ่มของอะไรสักอย่าง เช่น เซตของจำนวนเฉพาะ หมายถึง กลุ่มของจำนวนเฉพาะ ดังนั้น สิ่งที่อยู่ในเซตนี้จะต้องเป็นจำนวนเฉพาะเท่านั้น เช่น $3$ อยู่ในเซตของจำนวนเฉพาะ แต่ $4$ ไม่อยู่ในเซตของจำนวนเฉพาะ

ซึ่งการอยู่ในเซต เรียกว่า เป็นสมาชิก สัญลักษณ์ คือ $\in$

และถ้าไม่อยู่ในเซต เรียกว่า ไม่เป็นสมาชิก สัญลักษณ์ คือ $\notin$

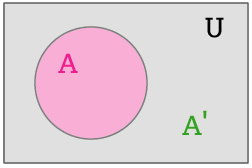
คอมพลีเมนต์ (Complement)

คอมพลีเมนต์ของเซต เป็นการดำเนินการที่แตกต่างจากยูเนียน อินเตอร์เซกชันและการลบกันของเซต เพราะคอมพลีเมนต์เป็นการดำเนินการบนเซตเซตเดียว โดยวิธีการคำนวณคอมพลีเมนต์ของเซตหนึ่งๆ ทำได้โดยการเอายูนิเวอร์สหรือเอกภพสัมพัทธ์เป็นตัวตั้งแล้วลบออกด้วยเซตนั้นๆ หรือพูดง่ายๆ ว่าการหาคอมพลีเมนต์ คือ การหาสมาชิกทั้งหมดที่ไม่อยู่ในเซตนั้น (แต่อยู่ในยูนิเวอร์ส) สัญลักษณ์ของคอมพลีเมนต์ มี 2 รูปแบบ คือ การเขียนชื่อเซตนั้นๆ ตามด้วยเครื่องหมายไพรม์ (′) หรือ อาจจะเขียนชื่อเซตนั้นๆ แล้วเขียนยกกำลังด้วยตัว c เช่น คอมพลีเมนต์ของเซต A เขียนแทนด้วย A′ หรือ Ac ก็ได้

ตัวอย่างการคำนวณคอมพลีเมนต์

ถ้ากำหนดเอกภพสัมพัทธ์เป็น U={0,1,2,3,⋯,9} และเซต A={0,2,4,6,8} กับ B={2,3,5,7} จงหา A′ และ Bc

พี่จะแสดงวิธีหา A′ โดยนำ U มาลบออกด้วย A ตามนี้นะครับ

A′====U−A{0,1,2,3,4,5,6,7,8,9}−{0,2,4,6,8}{0,1,2,3,4,5,6,7,8,9}{1,3,5,7,9}

ดังนั้น A′={1,3,5,7,9}

ส่วน Bc พี่จะใช้วิธีดูว่าสมาชิกใดบ้างที่ไม่อยู่ใน B แต่ยังอยู่ในยูนิเวอร์ส

เนื่องจากสมาชิกใน B ประกอบไปด้วยจำนวนเฉพาะบวกที่มีค่าไม่เกิน 10 ดังนั้นใน Bc จะต้องเป็นตัวเลขใน U ที่ไม่เป็นจำนวนเฉพาะซึ่งก็คือ

0,1,4,6,8 และ 9

ดังนั้น Bc={0,1,4,6,8,9}

A′={1,3,5,7,9} และ Bc={0,1,4,6,8,9}.

ยูนิเวอร์ส

เวลาเราพูดสิ่งกลุ่มของอะไรสักอย่าง จะต้องมีการบอกขอบเขต เช่น เวลาพูดถึงกลุ่มของผู้หญิง ก็จะต้องดูว่าเรากำลังพูดกลุ่มของผู้หญิงจากกลุ่มใหญ่กลุ่มไหน เช่น กลุ่มของผู้หญิง จาก นักเรียนในห้องหนึ่ง จะได้ว่ากลุ่มที่่ใหญ่ที่สุดที่เป็นขอบเขตในการกล่าวถึงกลุ่มอื่น ๆ ในทีนี้คือนักเรียนทั้งหมดในห้องหนึ่ง

ยูเนียน (Union)

บทนิยาม

เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B

ตัวอย่างเช่น A ={1,2,3}

B= {3,4,5}

∴ A ∪ B = {1,2,3,4,5}

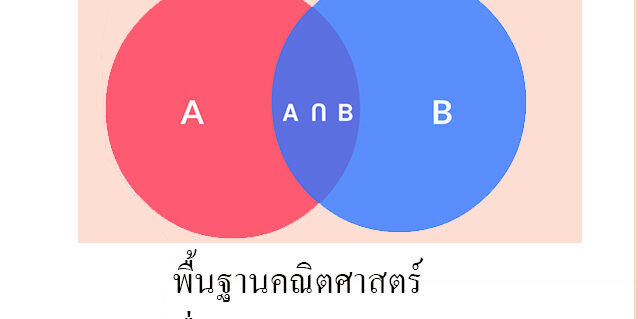
อินเตอร์เซกชัน (Intersection)

บทนิยาม

เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B

ตัวอย่างเช่น A ={1,2,3}

B= {3,4,5}

∴A ∩ B = {3}

คอมพลีเมนต์ (Complements)

บทนิยาม

ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’

ตัวอย่างเช่น U = {1,2,3,4,5}

A ={1,2,3}

∴A’ = {4,5}

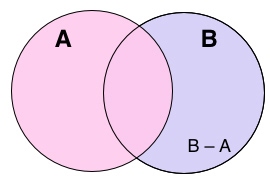
ผลต่าง (Difference)

บทนิยาม

ถ้าเซต A และ B เป็นเซตใดๆในเอกภพสัมพัทธ์ u เดียวกันแล้ว ผลต่างของเซต A และ B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A แต่ไม่เป็นสมาชิกของเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A – B

ตัวอย่างเช่น A ={1,2,3}

B= {3,4,5}

∴A – B = {1,2}