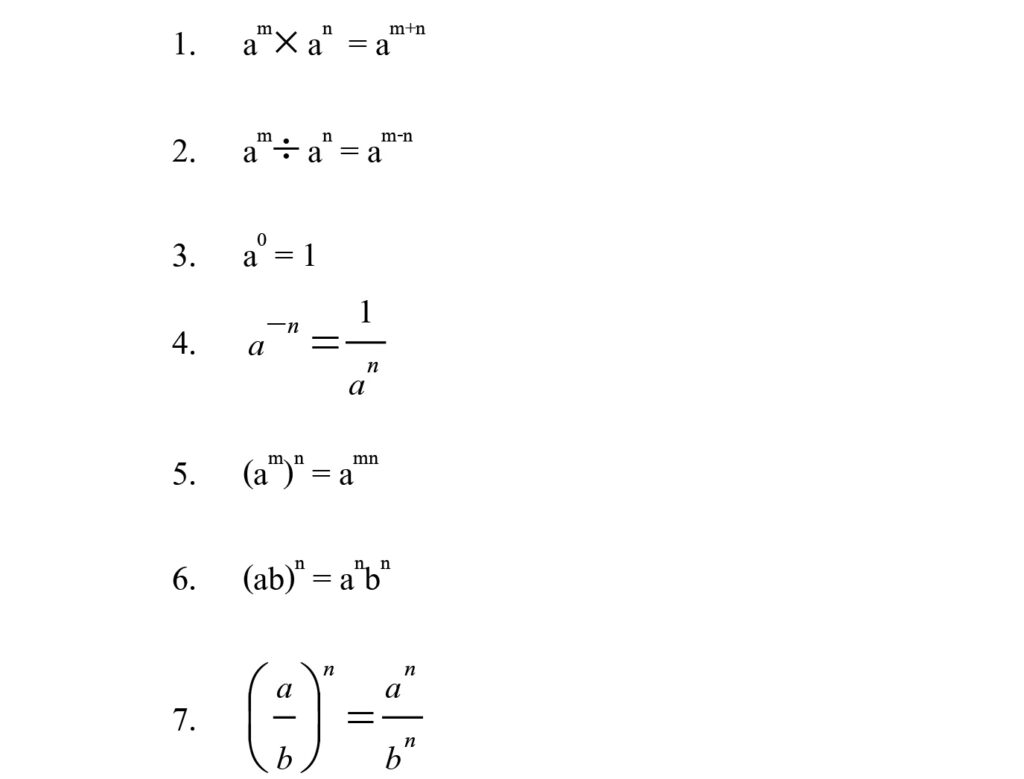เลขยกกำลังเบื้องต้น

สมบัติของเลขยกกำลัง

เมื่อ a และ b แทนจำนวนใดๆที่ไม่ใช่ศูนย์ m และn แทนจำนวนเต็ม

เลขยกกำลัง

ถ้าจำนวนที่คูณตัวเองซ้ำกันหลาย ๆ ตัว เราจะเขียนจำนวนเหล่านั้นออกมาในรูปของเลขยกกำลัง โดยจำนวนที่คูณตัวเองซ้ำ ๆ จะเรียกว่า “ฐาน” และจำนวนตัวที่คูณ จะเรียกว่า “เลขชี้กำลัง” เพื่อให้เข้าใจมากยิ่งขึ้น เพื่อน ๆ ลองนึกถึงการพับกระดาษ 1 แผ่น

พับกระดาษ 1 ครั้ง กระดาษถูกแบ่งออกเป็น 2 ส่วน

พับกระดาษ 2 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 = 4 ส่วน

พับกระดาษ 3 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 x 2 = 8 ส่วน

พับกระดาษ 10 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1,024 ส่วน

กระดาษพับซ้อนกัน 1,024 ทบนี่หนามาก ๆ เลย และในชีวิตจริง ถ้าต้องเขียน 2 x 2 x 2 x … x 2 ให้ครบตามต้องการก็คงจะเหนื่อยและเสียเวลามาก ๆ นักคณิตศาสตร์จึงนิยมเขียนออกมาในรูปของ “เลขยกกำลัง” ซึ่งประกอบไปด้วยฐานและเลขชี้กำลัง เราสามารถเขียน 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 ให้อยู่ในรูปเลขยกกำลังได้ว่า 2¹⁰ ซึ่ง 2 คือฐาน และ 10 คือเลขชี้กำลัง และจะอ่าน 2¹⁰ ว่า…

2 กำลัง 10

2 ยกกำลัง 10

หรือ กำลัง 10 ของ 2

เลขยกกำลัง ฐาน และเลขชี้กำลัง

จำนวนที่สามารถเป็นฐานได้มีหลายรูปแบบ เช่น จำนวนเต็มบวก จำนวนเต็มลบ เศษส่วน ทศนิยม ยกตัวอย่างเช่น 2⁴ (-2)⁴()²0.4⁵

ข้อสังเกต: อ่านไม่เหมือนกัน ผลลัพธ์ไม่เท่ากัน

ลบสองทั้งหมดยกกำลังสี่

(-2)⁴ = (-2)(-2)(-2)(-2) = 16

ลบสองยกกำลังสี่

-2⁴ = – (2 x 2 x 2 x 2) = -16

จะเห็นว่า (-2)⁴ มีค่าไม่เท่ากับ -2⁴ แค่ใส่วงเล็บ ผลลัพธ์ก็ต่างกันแล้ว ดังนั้นเพื่อน ๆ ต้องระวังการใส่วงเล็บให้ดีนะ เราลองมาดูตัวอย่างอื่น ๆ เพิ่มกันดีกว่า

5⁴ = 5 x 5 x 5 x 5 = 625

(5)⁴ = (5)(5)(5)(5) = 625

-5⁴ = -(5 x 5 x 5 x 5) = -(625) = -625

(-5)⁴ = (-5)(-5)(-5)(-5) = (25)(25) = 625

กรณีนี้ เลขชี้กำลังเป็นจำนวนคู่ สำหรับฐานที่เป็นจำนวนลบ จะเห็นว่า (-5)⁴ เท่ากับ 5⁴ แต่ไม่เท่ากับ -5⁴ อย่าลืมสังเกตให้ดีนะว่าเครื่องหมายลบอยู่ข้างในหรือข้างนอกวงเล็บ

5³ = 5 x 5 x 5 = 125

-5³ = -(5 x 5 x 5) = -125

(-5)³ = (-5)(-5)(-5) = -125

สมบัติอื่น ๆ ของเลขยกกำลัง

เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง

เราเคยเรียนเรื่องเลขยกกำลังที่มีฐานเป็นจำนวนใด ๆ มาแล้ว เช่น 8⁴ เป็นเลขยกกำลังที่มี 8 เป็นฐาน และ 4 เป็นเลขชี้กำลัง เราอาจเขียนแทน 8 ด้วย 2³

ดังนั้น 8⁴ อาจเขียนแทนด้วย (2³)⁴
(2³)⁴ เป็นเลขยกกำลังที่มี 2³ เป็นฐานและ 4 เป็นเลขชี้กำลัง

ให้พิจารณาความหมายของเลยยกกำลังที่มีฐานเป็นเลขยกกำลังต่อไปนี้
(5²)⁴ เป็นเลขยกกำลังที่มี 5² เป็นฐาน และ 4 เป็นเลขชี้กำลัง
(5²)⁴ = 5² × 5² × 5² × 5²
(5²)⁴ = 5^{(2 + 2 + 2 + 2)}
จะได้ (5²)⁴ = 5⁸ หรือ 5^{(2 × 4)}

จากการหาผลลัพธ์ของเลขยกกำลังข้างต้น จะสังเกตเห็นว่าเลขชี้กำลังของผลลัพธ์หาได้จากผลคูณของเลขชี้กำลังของฐานกับเลขชี้กำลังของเลขยกกำลังนั้น ซึ่งเป็นไปตามสมบัติของเลขยกกำลังดังนี้

เมื่อ a แทนจำนวนใด ๆ ที่ไม่ใช่ศูนย์ m และ n แทนจำนวนเต็ม
(a^m)ⁿ = a^mn

เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ

เราเคยทราบมาแล้วว่า 14³ เป็นเลขยกกำลังที่มี 14 เป็นฐานและ 3 เป็นเลขชี้กำลัง เราอาจเขียนแทน 14 ด้วย 2 × 7
ดังนั้น 14³ อาจเขียนแทนด้วย (2 × 7)³
(2 × 7)³ เป็นเลขยกกำลังที่มี 2 × 7 เป็นฐาน มี 3 เป็นเลขชี้กำลัง
พิจารณาความหมายของเลขยกกำลังที่มีฐานอยู่ในรูปการคูณของจำนวนหลาย ๆ จำนวนต่อไปนี้
(2 × 5)³ เป็นเลขยกกำลังที่มี 2 × 5 เป็นฐาน และ 3 เป็นเลขชี้กำลัง
(2 × 5)³ = (2 × 5) × (2 × 5) × (2 × 5)
(2 × 5)³ = (2 × 2 × 2) × (5 × 5 × 5)
(2 × 5)³ = 2³ × 5³
จะได้ (2 × 5)³ = 2³ × 5³

ผลที่ได้ข้างต้นเป็นไปตามสมบัติของเลขยกกำลัง ดังนี้
เมื่อ a แทนจำนวนใด ๆ ที่ไม่ใช่ศูนย์ และ n แทนจำนวนเต็ม
(ab)ⁿ = a^bbⁿ

เลขยกกำลังที่มีฐานอยู่ในรูปการหาร

ให้พิจารณาความหมายของเลขยกกำลังต่อไปนี้
(2 / 7)³ เป็นเลขยกกำลังที่มี 2 / 7 เป็นฐาน และมี 3 เป็นเลขชี้กำลัง
(2 / 7)³ = (2 / 7) × (2 / 7) × (2 / 7)
(2 / 7)³ = (2 × 2 × 2) / (7 × 7 × 7)
(2 / 7)³ = 2³ / 7³
จะได้ (2 / 7)³ = 2³ / 7³