สมบัติของจำนวนนับ (Property of counting Number)
สมบัติของจำนวนนับ มีเนื้อหาดังต่อไปนี้
(1) ตัวหารร่วมมากและการนำไปใช้
(2) ตัวคูณร่วมน้อยและการนำไปใช้บทที่ 2. ระบบจำนวนเต็ม
(1) จำนวนเต็ม
(2) การบวกจำนวนเต็ม
(3) การลบจำนวนเต็ม
(4) การคูณจำนวนเต็ม
(5) การหารจำนวนเต็ม
(6) สมบัติของจำนวนเต็มบทที่ 3. เลขยกกำลัง
(1) ความหมายของเลขยกกำลัง
(2) การดำเนินการของเลขยกกำลัง
(3) การนำไปใช้บทที่ 4. พื้นฐานทางเรขาคณิต
(1) จุด เส้นตรง ส่วนของเส้นตรง รังสีและมุม
(2) การสร้างพื้นฐาน
(3) การสร้างรูปเรขาคณิตอย่างง่าย3
จำนวนนับ
จำนวนนับ(Counting Number) หมายถึงจำนวนซึ่งเป็นที่รู้จักกันดีของมนุษย์และมนุษย์ได้นำเอาจำนวนดังกล่าวนั้นมาใช้เพื่อแสดงถึงจำนวนของสิ่งต่าง ๆ ได้แก่ 1, 2, 3, …
ข้อสังเกต
1. จำนวนนับจะต้องเริ่มจาก 1 เท่านั้น
2. จำนวนนับมีเลข 1 เป็นจำนวนที่น้อยที่สุด และมีค่าเพิ่มเรื่อย ๆ ไปทีละหนึ่งอย่างไม่มีที่สิ้นสุด ดังนี้ 1, 2, 3, 4, 5, …
สิ่งที่ควรทราบ
1. ระบบจำนวนนับ(Counting Number System) จะต้องประกอบไปด้วย 2 ส่วนหลัก ๆ คือ
1.1 เซตของจำนวนนับ N โดยที่ N = {1, 2, 3, 4, …}
1.2 ตัวกระทำ(Operation Code) คือ บวก(+) ลบ(-) คูณ(x) หาร(÷)
2. จำนวนนับ(Counter Number) บางครั้งอาจถูกเรียกว่า จำนวนธรรมชาติ(Natural Number)
การหารลงตัว
การหารจำนวนนับที่เป็นการหารลงตัว(Divisibility) ซึ่งมีลักษณะ ดังนี้
กำหนดให้ a และ b เป็นจำนวนนับ
พบว่า b หาร a ลงตัว ก็ต่อเมื่อมีจำนวนนับ c ที่ทำให้ a ÷ b = c
ข้อตกลง เรียก b ว่า ตัวหาร(Divisor) หรือ ตัวประกอบ(Factor) ของ a
และ เรียก a ว่า ตัวตั้ง(Dividened) หรือ พหุคูณ(Multiple) ของ b
ตัวอย่างการหารจำนวนนับที่เป็นการหารลงตัว เช่น
12 ÷ 3 = 4
จะพบว่า 3 หาร 12 ลงตัว
ข้อตกลง เรียก 3 ว่าตัวหาร หรือ ตัวประกอบของ 12
และ เรียก 12 ว่าตั้งตั้ง หรือ พหุคูณของ 3
สำหรับบทเรียนในชั้นนี้เราจะขอกล่าวถึงเฉพาะ การหารลงตัวที่มีลักษณะ a และ b เป็นจำนวนนับเท่านั้น ดังนั้นในระดับนี้จะพิจารณาเฉพาะการหารจำนวนนับที่เป็นการหารลงตัว ซึ่งมีลักษณะ a ÷ b = c
จำนวนเฉพาะ 1 – 100
- 2, 3, 5, 7, 11 และ 19 เป็นจำนวนเฉพาะหลัก
- 3, 7, 11 และ 19 เพิ่มครั้งละสิบ
- ทำการหารด้วย 3 และ 7 (ถ้าหารลงตัวไม่เป็นจำนวนเฉพาะ)
- จำนวนนับที่หารด้วย 7 ลงตัว มี 3 จำนวน คือ 49, 77 และ 91
- จำนวนเฉพาะที่ต้องจำ คือ 2, 3, 5, 7, 11 และ 19 ให้เป็นจำนวนเฉพาะหลัก
ตัวหารร่วมมาก (ห.ร.ม.) คือ ตัวหารร่วม (หรือตัวประกอบร่วม) ที่มีค่ามากที่สุด ที่นำไปหารจำนวนนับชุดใด(ตั้งแต่สองจำนวนขึ้นไป) ได้ลงตัว ต่อไปนี้เราจะเรียกว่าการหา ห.ร.ม. เช่น ห.ร.ม. ของ 8 และ 12 คือ 4 เพราะ 4 คือจำนวนที่มากที่สุดที่หารทั้ง 8 และ 12 ได้ลงตัว
วิธีการหา ห.ร.ม.
ตัวอย่าง จงหาห.ร.ม. ของ 4, 8 และ 12 วิธีการหา ห.ร.ม. มีด้วยกัน 3 วิธีดังนี้
1. พิจารณาตัวประกอบ ตัวประกอบของ 4 คือ 1, 2, 4 ตัวประกอบของ 8 คือ 1, 2, 4, 8 ตัวประกอบของ 12 คือ 1, 2, 3, 4, 6, 12 ตัวประกอบร่วมของ 4, 8 และ 12 คือ 1, 2, 4 ซึ่งตัวที่มากที่สุดก็คือ 4 ดังนั้น ห.ร.ม. คือ 4
2. วิธีแยกตัวประกอบ
4 = 2 x 2
8 = 2 x 2 x 2
12 = 2 x 2 x 3
เอาตัวที่ซ้ำมา ห.ร.ม. คือ 2 x 2 = 4
3. วิธีตั้งหาร
2 ) 4 8 12
2 ) 2 4 6
1 2 3 ห.ร.ม. คือ 2 x 2 = 4
ตัวหารร่วมมาก
หน่วยการเรียนรู้เรื่อง สมบัติของจำนวนนับ : ตัวหารร่วมมาก
จำนวนเฉพาะ คือ จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียง 2 ตัว คือ 1 และตัวเอง
ตัวประกอบเฉพาะ คือ ตัวประกอบที่เป็นจำนวนเฉพาะ
การแยกตัวประกอบของจำนวนนับใด ๆ คือ ประโยคที่แสดงการเขียนจำนวนนับนั้นในรูปการคูณของตัวประกอบเฉพาะ
ตัวหารร่วมมาก (ห.ร.ม.) ตัวหารร่วมมากของจำนวนสองจำนวนใด ๆ คือ จำนวนที่ต่างก็ไปหารจำนวนที่กำหนดให้นั้นได้ลงตัว เนื่องจากการหา ห.ร.ม. ของจำนวนนับตั้งแต่สองจำนวนขึ้นไปเป็นการหาตัวหารร่วม หรือตัวประกอบร่วมที่มากที่สุดของจำนวนนับแล้วนั้น
การหารลงตัว เช่น 15 3 = 5 เรียก 3 ว่า ตัวหาร หรือตัวประกอบของ 15
ตัวประกอบของจำนวนนับใด ๆ คือ จำนวนนับที่หารจำนวนนั้นลงตัว เช่น
ตัวประกอบทั้งหมดของ 10 ได้แก่ 1, 2, 5, 10
ตัวประกอบทั้งหมดของ 12 ได้แก่ 1, 2, 3, 14, 6, 12
จะเห็นว่า 1 และ 2 เป็นตัวประกอบของทั้ง 10 และ 12 จึงเรียก 1 และ 2 ว่าตัวประกอบร่วม หรือ ตัวหารร่วมของ 10 และ 12
เนื่องจาก 1 หารจำนวนนับทุกจำนวนลงตัว ดังนั้น 1 จึงเป็นตัวประกอบร่วมของจำนวนนับ
ทุกจำนวน
จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียง 2 ตัว คือ 1 และตัวเองเรียกว่าจำนวนเฉพาะ
ตัวประกอบที่เป็นจำนวนเฉพาะ เรียกว่า ตัวประกอบเฉพาะ
เช่น 3 และ 5 เป็นตัวประกอบเฉพาะของ 15 เป็นต้น
การแยกตัวประกอบของจำนวนนับใด ๆ คือ ประโยคที่แสดงการเขียนจำนวนนับนั้นในรูปการคูณของตัวประกอบเฉพาะ เช่น 12 = 2 × 2 × 3
18 = 2 × 3 × 3
จากการแยกตัวประกอบข้างต้น จะเห็นว่าตัวประกอบร่วม หรือตัวหารร่วมของ 12 และ 18 คือ 2, 3, และ 6
ตัวหารร่วมมาก (ห.ร.ม.)
ตัวหารร่วมมากของจำนวนสองจำนวนใดๆ คือ จำนวนที่ต่างก็ไปหารจำนวนที่กำหนดให้นั้นได้ลงตัว เนื่องจากการหา ห.ร.ม. ของจำนวนนับตั้งแต่สองจำนวนขึ้นไปเป็นการหาตัวหารร่วม หรือตัวประกอบร่วมที่มากที่สุดของจำนวนนับแล้วนั้น เราจึงอาศัยการหาตัวประกอบร่วมในการหา ห.ร.ม. ของจำนวนนับได้โดยวิธีต่างๆ ดังนี้
ตัวอย่างที่ 1 จงหา ห.ร.ม. ของ 6 และ 18
วิธีที่ 1 โดยการพิจารณาตัวประกอบ
เนื่องจาก ตัวประกอบของ 6 ได้แก่ 1, 2, 3, 6
ตัวประกอบของ 18 ได้แก่ 1, 2, 3, 6, 9, 18
ตัวประกอบร่วมของ 6 และ 18 ได้แก่ 1, 2, 3 และ 6
ตัวประกอบร่วมที่มากที่สุดของ 6 และ 18 คือ 6
ดังนั้น ห.ร.ม. ของ 6 และ18 คือ 6
วิธีที่ 2 โดยการแยกตัวประกอบ
6 = 2 × 3
18 = 2 × 3 × 3
จากการแยกตัวประกอบของ 6 และ 18 จะได้ว่า ตัวประกอบร่วมของ 6 และ 18
ได้แก่ 2, 3 และ 2 × 3 ตัวประกอบร่วมที่มากที่สุดของ 6 และ 18 คือ 2 × 3 = 6
ดังนั้น ห.ร.ม. ของ 6 และ18 คือ 6
วิธีที่ 3 โดยการตั้งหาร
2 ) 6 18
3 ) 3 9 1 3
ห.ร.ม.ของ 6 และ18 หาได้จาก 2 × 3 = 6
ดังนั้น ห.ร.ม. ของ 6 และ18 คือ 6
ข้อสังเกต
1. ในแต่ละขั้นตอนของการหาร จำนวนที่นำไปหารต้องเป็นจำนวนเฉพาะที่เป็นตัวประกอบร่วมของ
ทุกจำนวนที่ต้องการหาร ซึ่งอาจมีหลายจำนวน เลือกจำนวนเฉพาะจำนวนใดจำนวนหนึ่งไปหารก่อนก็ได้ 2. การหารจะยุติเมื่อไม่มีจำนวนเฉพาะที่เป็นตัวประกอบร่วมของทุกจำนวนที่ต้องการ
3. ห.ร.ม. ที่ได้ คือ ผลคูณของจำนวนเฉพาะที่นำไปหารในแต่ละขั้นตอน
ตัวอย่างที่ 2 จงหา ห.ร.ม. ของ 6, 20 และ 30
วิธีที่ 1 โดยการพิจารณาตัวประกอบ
เนื่องจาก ตัวประกอบของ 6 ได้แก่ 1, 2, 3, 6
ตัวประกอบของ 24 ได้แก่ 1, 2, 3, 4, 6, 8, 12, 24
ตัวประกอบของ 30 ได้แก่ 1, 2, 3, 5, 6, 10, 15, 30
ตัวประกอบร่วมของ 6, 24 และ 30 ได้แก่ 1, 2, 3 และ 6
ตัวประกอบร่วมที่มากที่สุดของ 6, 24 และ 30 คือ 6
ดังนั้น ห.ร.ม. ของ 6, 24 และ 30 คือ 6
วิธีที่ 2 โดยการแยกตัวประกอบ
6 = 2 × 3
24 = 2 × 3 × 2 × 2
30 = 2 × 3 × 5
จากการแยกตัวประกอบของ 6, 24 และ 30 จะได้ว่า
ตัวประกอบร่วมที่มากที่สุดของ 6, 24 และ 30 คือ 2 × 3 = 6
ดังนั้น ห.ร.ม. ของ 6, 24 และ 30 คือ 6
วิธีที่ 3 โดยการตั้งหาร
2 ) 6 24 30
3 ) 3 12 15
1 4 5
ห.ร.ม.ของ 6, 24 และ 30 หาได้จาก 2 × 3 = 6
ดังนั้น ห.ร.ม. ของ 6, 24 และ 30 คือ 6
การยกกำลัง (อังกฤษ:Exponentiation)
การยกกำลัง (อังกฤษ:Exponentiation) คือ การดำเนินการทางคณิตศาสตร์อย่าง
หนึ่งเขียนอยูู่่ในรูป ![]() ซึ่งประกอบด้วยสองจำนวน คือ ฐาน a และ เลขชี้กำลัง n โดย
ซึ่งประกอบด้วยสองจำนวน คือ ฐาน a และ เลขชี้กำลัง n โดย
พื้นฐานแล้วการยกกำลังจะมีความหมายเหมือนกับการคูณ a ซ้ำๆเป็นจำนวน n ตัว เมื่อ n
เป็นจำนวนเต็มบวก
คือ การคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) จะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa)
ตัวอย่าง
25 เป็นเลขยกกำลัง ที่มี 2 เป็นฐานหรือตัวเลข และมี 5 เป็นเลขชี้กำลัง
และ 25 = 2x2x2x2x2 = 32
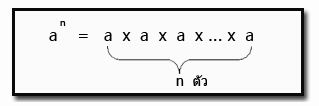

นิยาม ถ้า a เป็นจำนวนใด ๆ และ n เป็นจำนวนเต็มบวก “ a ยกกำลัง n “ หรือ “ a กำลัง n “
เขียนแทนด้วย aมีความหมายดังนี้ a= aaaaa …..a (a คูณกัน n ตัว)
จากนิยาม จะเรียก aว่าเลขยกกำลัง เรียก a ว่า ฐาน และเรียก n ว่า เลขชี้กำลัง
ตัวอย่าง เช่น 1) 3 = 3333 มี 3 เป็น ฐาน และ มี 4 เป็นเลขชี้กำลัง
2) (-5) = -5-5-5 มี -5 เป็น ฐาน และ มี 3 เป็นเลขชี้กำลัง
3) = มี เป็น ฐาน และ มี 2 เป็นเลขชี้กำลัง






